알고리즘의 성능은 구조를 어떻게 설계하였고 어떤 자료구조를 사용했는가에 따라서 그 성능이 달라진다 그래서 이 알고리즘의 성능을 측정하기 위한 방법에는 시간복잡도 분석 , 공간복잡도 분석이 있다
시간 복잡도 분석 : 수행 시간을 분석
공간 복잡도 분석 : 수행 시 필요로 하는 메모리 공간 분석
시간 복잡도
알고리즘을 이루고 있는 연산들이 몇번이나 수행되는 지를 숫자로 표시하고 입력의 개수 n개에 대한 시간복잡도 함수를 T(n) 이라고 표시한다
예시 : n을 n번 더하는 문제
- n*n
- for 문을 이용하여 n을 n번 더함
- 이중 for문을 이용하여 1을 n*n번 더함
위 3개의 알고리즘을 이용하여 시간복잡도 함수를 비교해보면 아래와 같다
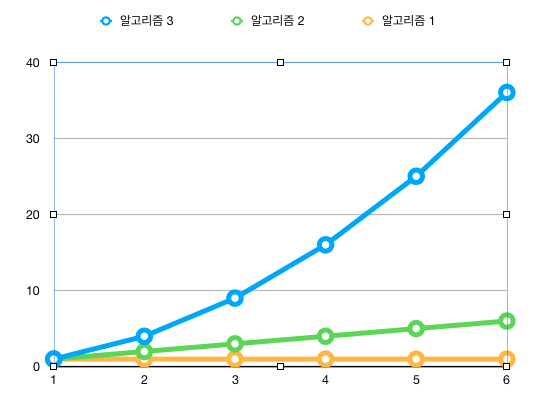
빅오 표기법
자료의 개수가 엄청나게 많은 경우에 시간복잡도 함수를 계산하게 되면 가장 큰 항의 영향력이 다른 항에 영향을 무시될 정도로 작아진다
예를 들어 n= 1,000,000 이고 T(n) = n^2 +n+1 일 때 T(n)은 1,000,001,000,001 이고 이 중에서 첫번재 항의 비율을 99%이다 이런 특징을 고려해서 연산의 횟수를 대략적으로 표시하기로 한 방식이 빅오 표기법이다
- 빅오 표기법을 이용해서 알고리즘의 성능을 측정할 때에는 최악의 경우를 고려하는 것이 중요한 의미가 될 수 있다
각 자료 구조의 시간 복잡도
배열
배열의 일반적인 구조는 아래와 같이 연속된 공간이 선형으로 이어져 있는 자료 구조 이다

이렇게 이어져 있는 배열의 특징은 컴퓨터가 인덱스( 요소의 위치 ) 를 기억하고 있다는 것이다 이런 특징으로 인해 다음 연산들의 성능이 좋다
- 요소를 조회 하는 연산 → o(1)
- 요소에 할당 하는 연산 → o(1)
위와 같은 연산들에서 성능이 좋지만 요소를 삽입하고 삭제하고 찾는 연산은 O ( n ) 만큼의 시간이 걸린다
연결리스트
연결리스트의 경우 배열과 비슷하게 선형의 자료구조 이지만 각각의 노드는 배열과 같은 인덱스가 있는 것이 아니라 다음 노드에 대한 정보만을 이용해 구성된 자료구조이다
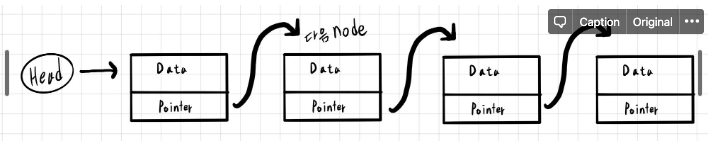
연결리스트의 경우 이런 특징 때문에 요소를 삽입 삭제 하는 경우에 O(1) 의 시간이 걸린다 그 이유는 요소를 삽입과 삭제하는 과정에 단순히 몇번의 링크만 변경해주면 되기 때문이다
배열과 반대로 연결리스트는 인덱스가 없기 때문에 조회 ,할당, 탐색 연산의 시간이 o ( n ) 만큼 걸린다
연결리스트와 배열의 trade off
- 특정 위치를 찾는 것은 배열이 좋고
- 삽입하는 과정은 연결리스트가 좋다
- 리스트 끼리는 더블 연결 리스트가 효율성이 좋지만 공간을 많이 차지한다.
트리
트리는 계층적인 구조를 가지는 자료구조이다
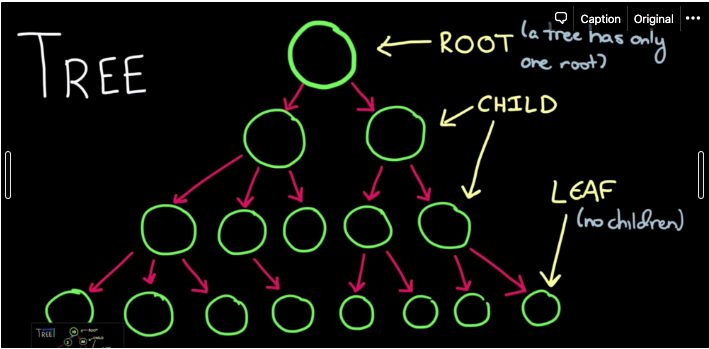
위와 같은 구조를 가진 트리에서 만약 값을 찾아야 한다면 모든 노드를 찾아야 할 것 이고 인는 O(n)의 시간복잡도를 가질 것이다
이와 다르게 binary search tree의 경우 탐색 속도가 매우 빨라 진다 그 이유는 아래와 같은 구조를 가지고 있기 때문이다
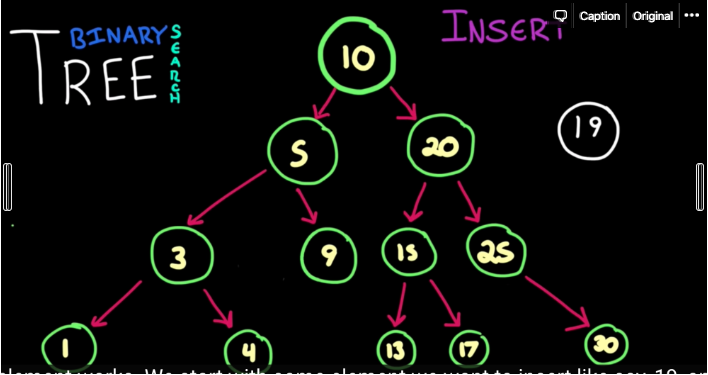
위와 같이 밸런스가 맞게 되어 있는 binary search tree 의 경우 탐색 연산의 o(logn) 시간이 걸린다 이런 특성을 유지하기 위해서는 트리의 밸러스를 맞춰야 하는 데 만약 밸런스가 안 맞은 트리의 성능은 연결 리스트와 똑같다
이제 이 밸런스를 구하는 방법은 양쪽의 서브 트리의 깊이의 차를 이용해서 구한다 이 깊이의 차가 1 이상으로 넘어가는 경우 밸런스를 맞춰 줘야 한다 밸런스를 맞추는 방법에는 여러가지가 있다
- AVL 트리
- Red-black 트리
해쉬 테이블
해쉬 테이블은 키를 hash 함수를 이용하여 연산 후 나온 값을 인덱스를 이용하여 값을 저장하는 자료구조 이다
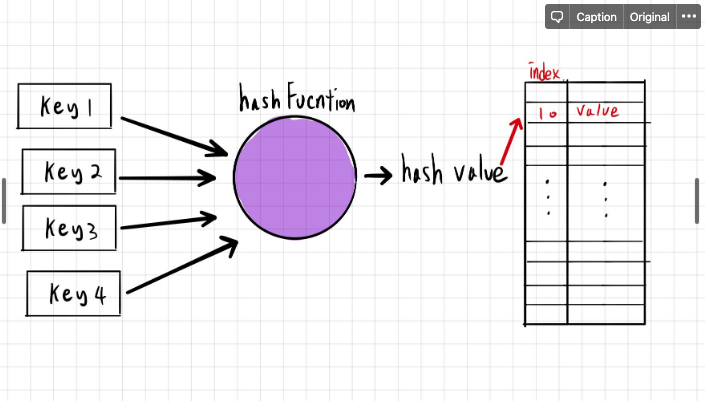
- 삽입 : 삽입의 경우 hash 함수에서 나온 인덱스에 그대로 대입하면 되기 때문에 o(1) 이다
- 삭제 : 삭제의 경우 hash 함수에서 나온 인덱스를 그대로 삭제하면 되기 때문에 o(1) 이다
- 탐색 : 키를 알고 있으면 이를 이용해서 값을 찾을 수 있기 때문에 o(1) 이다
해쉬 테이블의 경우 성능면에서 좋은 것은 맞으나 삽입 연산을 실행 할 때 충돌이 일어난 경우를 생각해 보면 최악의 경우 모든 테이블에서 충돌이 일어날 수 있다 이 경우 o(n)이다