각각의 학생들은 파티에 참석하기 위해 걸어가서 다시 그들의 마을로 돌아와야 한다. 하지만 이 학생들은 워낙 게을러서 최단 시간에 오고 가기를 원한다.

파티가 열리는 곳까지의 거리가 가장 긴 학생을 찾는 문제지만,
학생은 게으르다.......
즉 파티까지의 최단거리가 가장 긴 학생을 찾아야 한다.

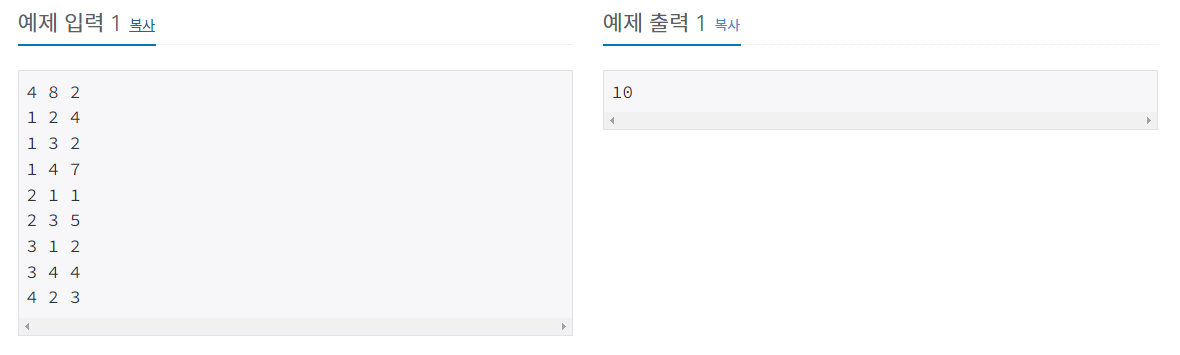
예제 입력을 가지고 문제를 해석해보자.

아래의 두 값을 더함으로써 1, 3, 4 집에 사는 각 학생들이 2번집에 다녀오는 최단거리를 구할 수 있다.

• 1) 2번집에서 오는 최단거리
• 2) 2번집까지 가는 최단거리

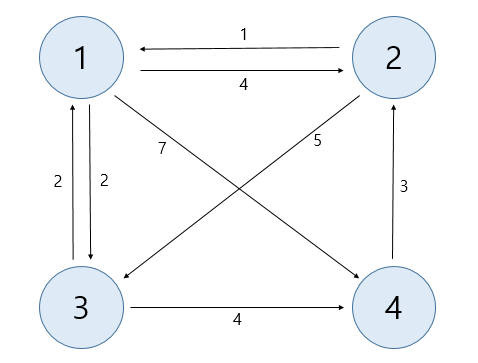
1) 2번집에서 각자의 집으로 돌아가는 최단거리는 예제 입력을 인접리스트로 저장하여 2번 집에서 시작하는 다익스트라 알고리즘을 적용하여 구할 수 있다.


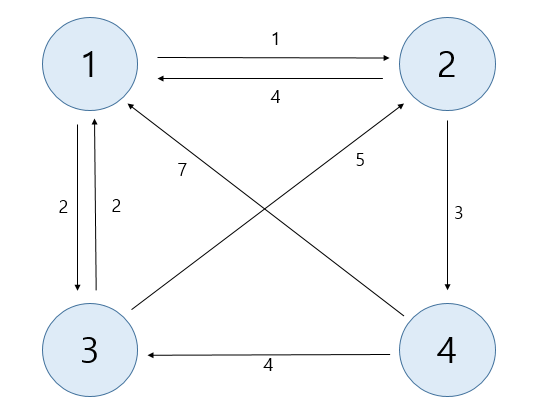
2) 각자의 집에서 2번집으로 가는 최단거리는 그래프 간선의 방향을 모두 반대로 바꾼뒤, 2번 집에서 시작하는 다익스트라 알고리즘을 적용하여 구한값과 같다.

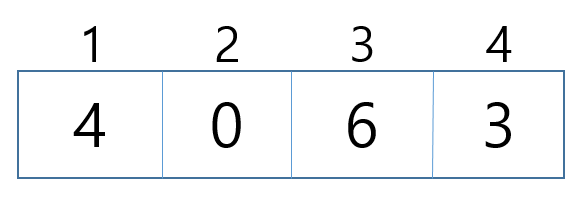
• 최종적으로 1), 2) 에서 구한 두 배열을 합한 뒤, 최댓값을 찾는다.

구현

import java.util.*;

/* 1238 파티 (다익스트라) */
public class Main {

    static class Edge implements Comparable<Edge>{
        int vex;
        int cost;
        public Edge(int vex, int cost) {
            this.vex = vex;
            this.cost = cost;
        }
        @Override
        public int compareTo(Edge o) {
            return this.cost - o.cost;
        }
    }

    static int[] toparty;
    static int[] tohome;
    static ArrayList<ArrayList<Edge>> graph_foward;	
    static ArrayList<ArrayList<Edge>> graph_backward;
    
    // 다익스트라
    public static void dijkstra(int v, int[] dis, ArrayList<ArrayList<Edge>> graph){
        PriorityQueue<Edge> pQ = new PriorityQueue<Edge>();
        dis[v] = 0;
        pQ.offer(new Edge(v,0));
        while(!pQ.isEmpty()){
            Edge tmp = pQ.poll();
            int now = tmp.vex;
            int nowCost = tmp.cost;
            if(dis[now] < nowCost) continue;
            for(Edge ob : graph.get(now)){
                if(dis[ob.vex] > ob.cost + nowCost) {
                    dis[ob.vex] = ob.cost + nowCost;
                    pQ.offer(new Edge(ob.vex, ob.cost+nowCost));
                }
            }
        }
    }
    
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        int n = sc.nextInt();
        int m = sc.nextInt();
        int x = sc.nextInt();

        toparty = new int[n+1];
        tohome = new int[n+1];

        Arrays.fill(toparty, Integer.MAX_VALUE);
        Arrays.fill(tohome, Integer.MAX_VALUE);

        graph_foward = new ArrayList<ArrayList<Edge>>();
        graph_backward = new ArrayList<ArrayList<Edge>>();

        for(int i=0; i<=m; ++i) {
            graph_foward.add(new ArrayList<Edge>());
            graph_backward.add(new ArrayList<Edge>());
        }
        for(int i=0; i<m; ++i){
            int a = sc.nextInt();
            int b = sc.nextInt();
            int c = sc.nextInt();
            graph_foward.get(a).add(new Edge(b,c));	
            graph_backward.get(b).add(new Edge(a,c));	// 간선정보가 거꾸로된 그래프 저장
        }

        dijkstra(x, toparty, graph_backward);	// 집 > 파티  최단경로 탐색
        dijkstra(x, tohome, graph_foward);		// 파티 > 집  최단경로 탐색

        int[] total = new int[n+1];
        for(int i=1; i<=n; ++i)
            total[i] = toparty[i] + tohome[i];
        System.out.println(Arrays.stream(total).max().getAsInt());
    }
}