[코딩테스트 공부] 조합

출처 : https://www.acmicpc.net/problem/15650

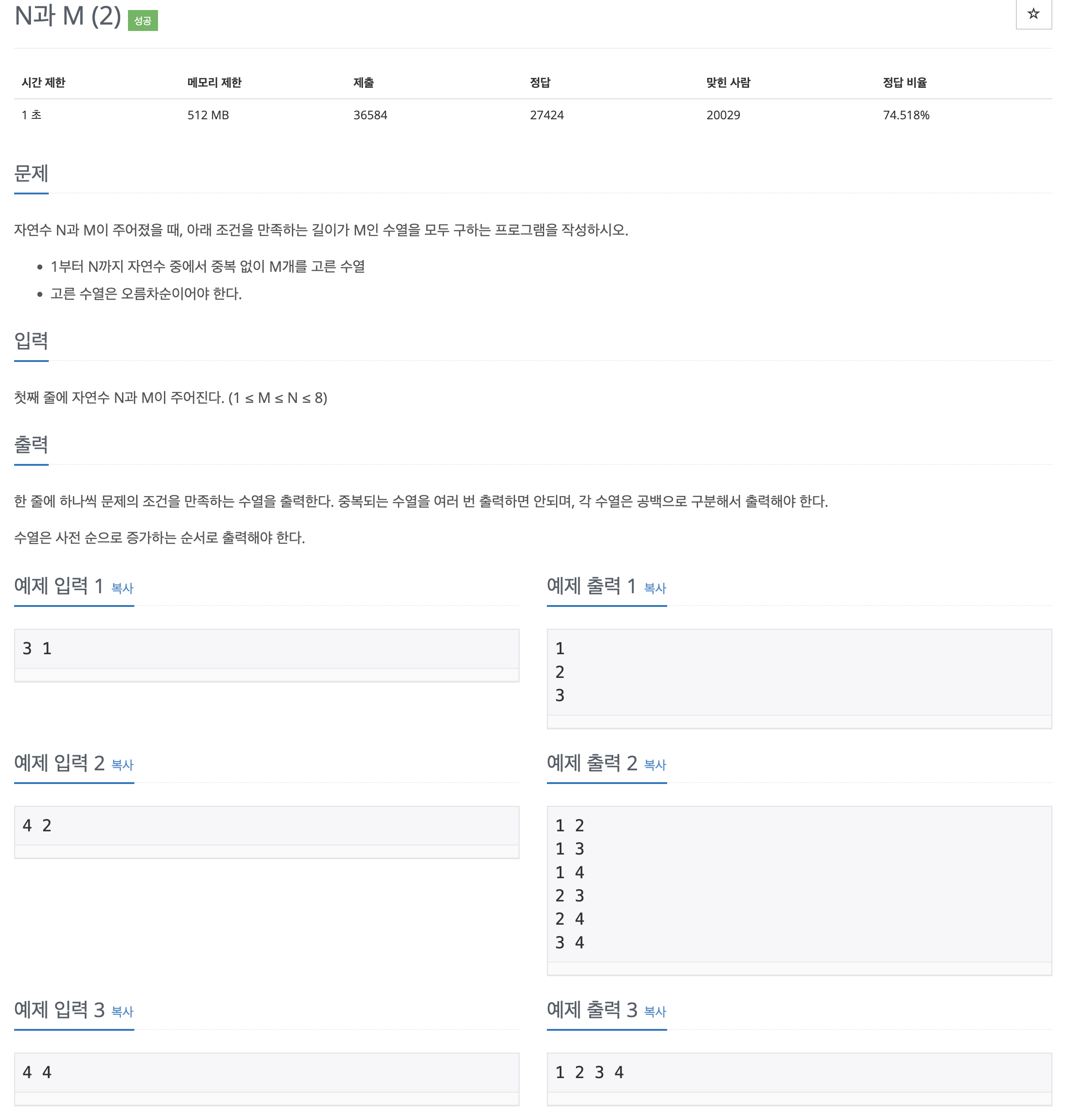
풀기 전에 생각을 해봅시다

우리는 현실 세계에서 숫자를 조합할 때, 숫자를 하나 고른 다음에 다음 숫자부터 조합을 수행합니다.

예를 들어서, 이런 알고리즘을 현실에서 사용하고 있습니다

1 2 3 4 5 -> 1
2 3 4 5 -> 1 2
.
.
.

따라서, 우리도 이 알고리즘을 구현할 때는, 재귀함수로 구현하되, 이전에 고른 숫자를 기억해서 다음 인덱스부터 범위를 좁혀서 탐색하는 전략을 채택하면 되는 것을 알 수 있습니다.

코드를 확인해볼까요?

def get_combination_sequences(k, given_length, start_number, partial_sequence):
    # 탈줄 조건
    if k == given_length:
        print(partial_sequence)
        return
    elif start_number > N:
        return
    
    # 점화식
    for i in range(start_number, N + 1):
        sequence_param = partial_sequence + str(i) + " "
        get_combination_sequences(k + 1, given_length, i + 1, sequence_param)
    
N, M = map(int, input().split(" "))
get_combination_sequences(0, M, 1, "")

코드 해설

get_combination_sequence 메소드의 파라미터부터 분석해보겠습니다

• k : 현재 재귀함수의 진행 현황
• given_length : 출력해야하는 조합의 길이 -> 탈출조건으로 사용
• start_number : 탐색해야하는 첫 숫자가 무엇인가?
• partial_sequence : 현재 탐색한 숫자들을 저장한 문자열

다음으로, 탈출조건을 분석해보겠습니다.

    if k == given_length:
        print(partial_sequence)
        return
    elif start_number > N:
        return

첫번째로, k == given_length의 경우, 모든 조합이 완성된 상태이므로 print를 하고 return을 수행하면 됩니다.

두번째 조건으로, start_number가 N을 넘어가는 경우(조합을 하다가 start_number가 정해진 인덱스를 넘어가는 경우)에는 조합이 완성될 수 없으므로, 그냥 return해주면 됩니다.

점화식은 매우 간단합니다.

    for i in range(start_number, N + 1):
        sequence_param = partial_sequence + str(i) + " "
        get_combination_sequences(k + 1, given_length, i + 1, sequence_param)

위에서 말했던 전략처럼, 숫자를 하나 고르게 된 경우, 그 숫자 이후로 범위를 좁혀서 탐색해주면 되기 때문에, start_number 자리에 i + 1을 전달하여 다음 k로 보내주는 것을 확인할 수 있습니다.