[Java] Lv.3 프로그래머스 입국 심사

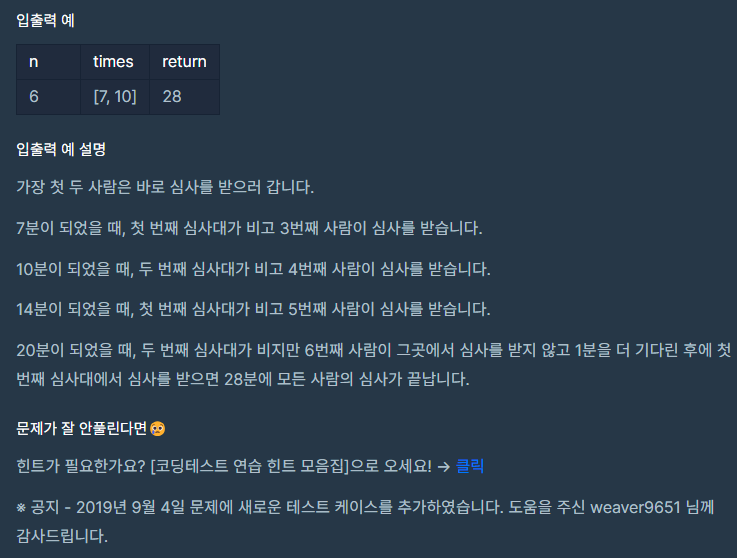
설명

일단 제한사항을 보면 최악이 10억이다. 완전탐색은 안된다.
10억이면 O(n) 도 안되기에...

O(log n) 으로 가야한다.

이 문제는 이진 탐색으로 풀 수 있는 문제인데 어디를 기준으로 잡아할지 파악 하는게 핵심인 것 같다.

일단 이진 탐색을 하려면 탐색할 기준이 있어야 하고, 기준을 중심으로 시작과 끝이 있어야 반으로 나누고 다시 탐색을 진행하는 방식인데...

핵심은 K분 안에 모든 사람이 심사를 받을 수 있는가? 이다.
즉 시간 이 기준점이 된다.

예제로 설명을 하면
n = 6 times[7, 10] 일 때

s(시작) = 1 		e(끝) = 60

시작이 1인 이유는 제일 작은 수가 1부터 시작하기 때문. 사람이 1명일 때 심사관도 무조건 1명
끝은 times 배열에서 제일 오래 걸리는 심사관(10) * 사람수(6)
최악일 경우 제일 오래 걸리는 심사관에게 모든 사람이 심사를 받을 수 있으므로.

그림으로 표현하면 아래와 같다.

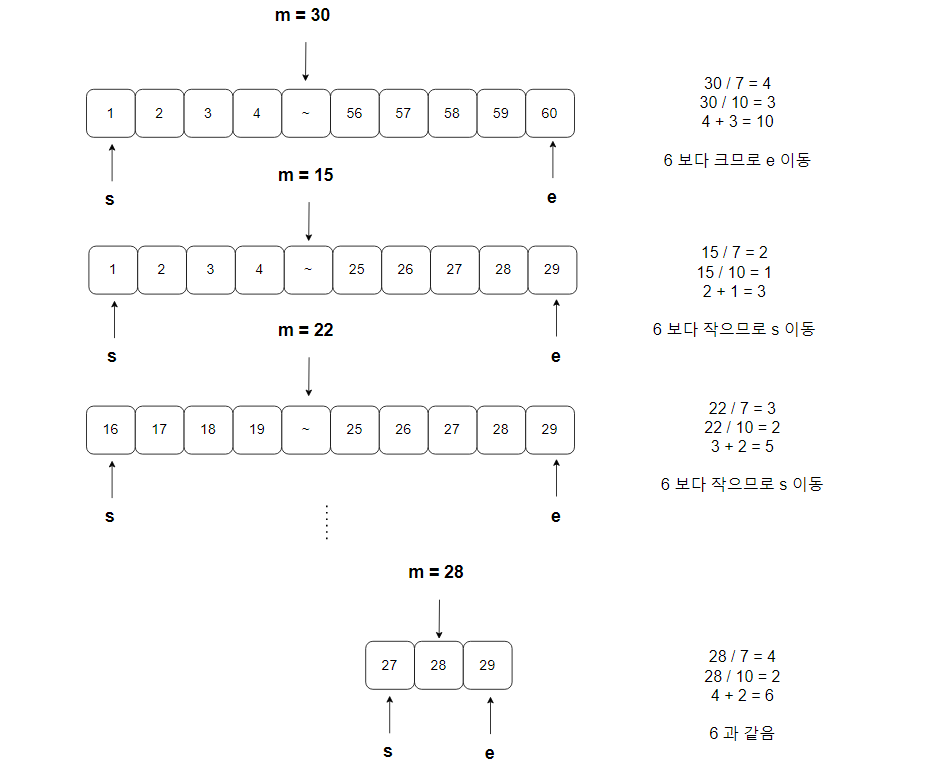
틀린 코드

class Solution {
    public long solution(int n, int[] times) {
        long answer = 0;
        long start = 1;
        long end = (times[times.length -1]) * (long) n;

        while (start <= end) {
            long a = 0;
            long mid = (start + end) / 2;
            for (int i = 0; i < times.length; i++) {
                a += mid / times[i];
            }
            if (a > n) {
                end = mid -1;
            } else if (a < n) {
                start = mid + 1;
            } else {
                answer = mid;
                start = mid + 1;
                end = mid - 1;
            }
        }
        return answer;
    }
}

그래요 이 코드...
예시는 돌아갑니다..하지만 제출을 누르면?

네 왜인지 모르겠지만 예제빼고 다 틀려버리죠.

코드

import java.util.*;
class Solution {
    public long solution(int n, int[] times) {
        long answer = 0;
        long start = 1;
        long end = times[times.length -1] * (long) n;

        while (start <= end) {
            long a = 0;
            long mid = (start + end) / 2;
            for (int i = 0; i < times.length; i++) {
                a += mid / times[i];
            }
            if (a >= n) {
                end = mid -1;
                answer = mid;
            } else if (a < n) {
                start = mid + 1;
            } 
        }
        return answer;
    }
}

이 코드로 성공했다

오! 11점이라니!! 신기방기