
https://www.acmicpc.net/problem/11659
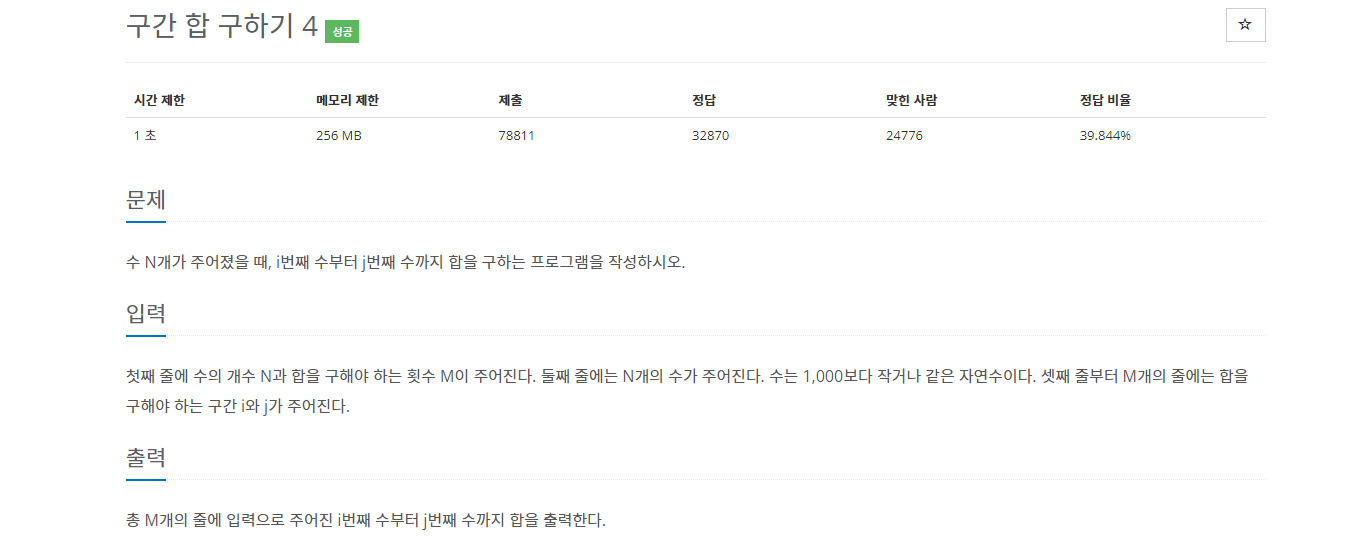
제한
1 ≤ N ≤ 100,000
1 ≤ M ≤ 100,000
1 ≤ i ≤ j ≤ N
예제입력
5 3
5 4 3 2 1
1 3
2 4
5 5예제 출력
12
9
1설명
길이 n의 배열을 m 횟수 만큼 더해서 값을 출력하는 문제이다.
예제를 그림으로 보자면
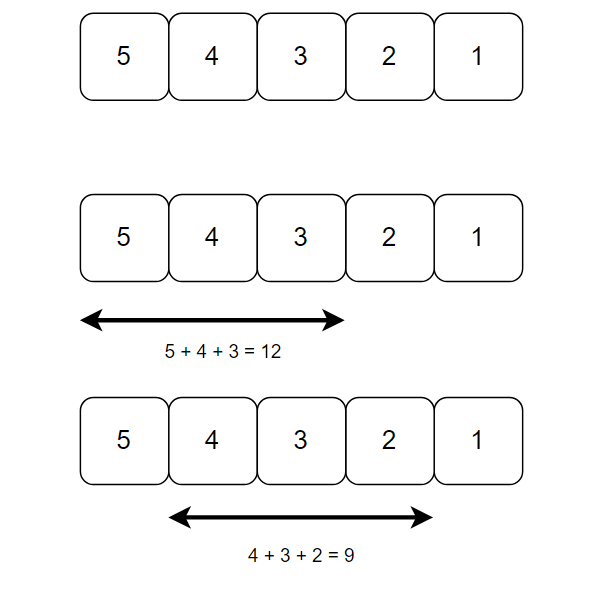
5에서 1까지의 배열이 있고
1번부터 3번까지의 숫자는 5,4,3이므로 더하면 12가 될 것이고,
2번부터 4번까지의 숫자는 4,3,2 이므로 더하면 9가 될 것이다.
이럴 때 합배열을 사용할 수 있다.
합배열이란 이전배열까지의 합을 저장해놓은 배열을 뜻한다.
예시의 배열을 합배열로 만들면 이렇게 된다.
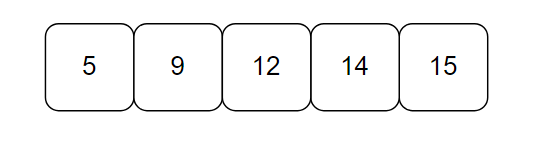
합배열을 만드는 공식은 D[i] = D[i-1] + A[i] 이다
이게 무슨 말이냐면
5,4,3,2,1 배열이 있을 때
맨 처음
D[1] = D[1-1] + A[1] 은 = 0 + 5 = 5일 것이고,
두 번째
D[2] = D[2-1] + A[2] 는 (D의 1번째 인덱스 값(5)) 5 + 4 = 9 일 것이고,
세 번째
D[3] = D[3 -1] + A[3] 은 (D의 2번째 인덱스 값(9)) 9 + 3 = 12 일 것이고,
네 번째
D[4] = D[4 -1] + A[4] 는 (D의 3번째 인덱스 값(12)) 12 + 2 = 14 일 것이고,
마지막
D[5] = D[5 -1] + A[5] 는 (D의 4번째 인덱스 값(14)) 14 + 1 = 15 가 된다.
이렇게 합 배열을 만들어 놓고,
구간 합을 구하면 굉장히 간단하게 정답을 구할 수 있다.
구간 합을 구하는 공식은 D[j] - D[i -1] 이다.
예로들어서 1부터 3까지의 합을 출력하라고 했을 경우
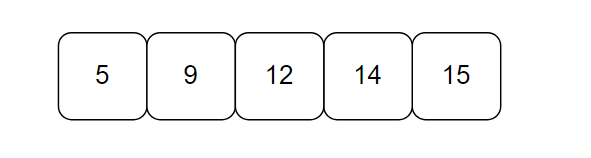
합 배열에서 D[3] - D[1 -1] 은 12 - 0 = 0 이므로 답은 12가 된다.
2부터 4까지의 합을 출력한다면
합 배열에서 D[4] - D[2 -1] 은 14 - 5 = 9 이므로 답은 9가 된다.
이렇게 합 배열에서 구간 합을 구하는 공식이 D[j] - D[i -1] 인 이유는
1부터 3까지의 합이라고 했을 때
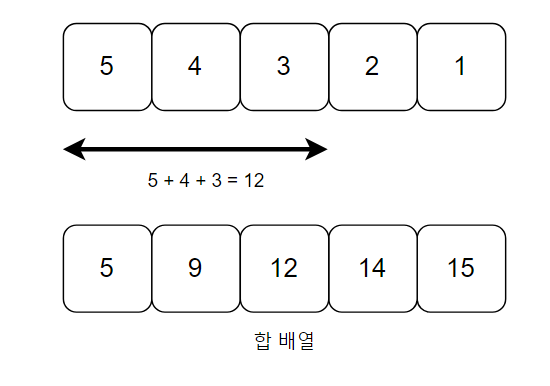
합 배열[j] 에는 1부터 3까지의 합이 들어있다. 그러니 [i] 에서 -1 을 해준 그 전 값을 빼면 그 사이의 합이 나오는 것이다.
코드
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
// int 수의 길이 변수 선언과 동시에 입력 받기
int length = Integer.parseInt(st.nextToken());
// int 합의 횟수 변수 선언과 동시에 입력 받기
int sNum = Integer.parseInt(st.nextToken());
// int[] arr 1차원 배열 선언
long[] arr = new long[length + 1];
st = new StringTokenizer(br.readLine());
// for (수의 변수만큼 반복 ) {
for (int i = 1; i <= length; i++) {
int a = Integer.parseInt(st.nextToken());
arr[i] = arr[i-1] + a;
}
// 합 배열 생성 d[i] = d[i-1] + a[i]
// }
for (int a = 0; a < sNum; a++) {
st = new StringTokenizer(br.readLine());
int i = Integer.parseInt(st.nextToken());
int j = Integer.parseInt(st.nextToken());
// 구간 합 계산 d[j] - d[i-1]
System.out.println(arr[j] - arr[i-1]);
}
}
}
