[Java] 백준 1325 효율적인 해킹

문제 링크 : https://www.acmicpc.net/problem/1325

풀이

이번 문제는 BFS 알고리즘 으로 풀었다.

시간제한이 5초로 BFS 알고리즘O(V+E)으로 풀어도 넉넉하다.

A가 B를 신뢰하는 경우 B를 해킹하면 A도 해킹 할 수 있다는 말은 단방향 그래프 라는 의미이다.
따로 가중치가 없으므로 가중치가 없는 단방향 그래프.

예제를 보자.

n = 5, m = 4 (노드, 에지)
3 -> 1
3 -> 2
4 -> 3
5 -> 3

그림으로 보면

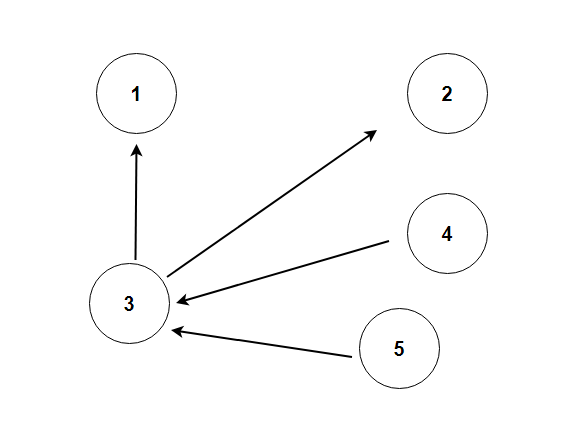
이런 그래프가 된다.

인접 리스트 
1 -> 
2 -> 
3 -> 1, 2
4 -> 3
5 -> 3

BFS 로 표현해보자.

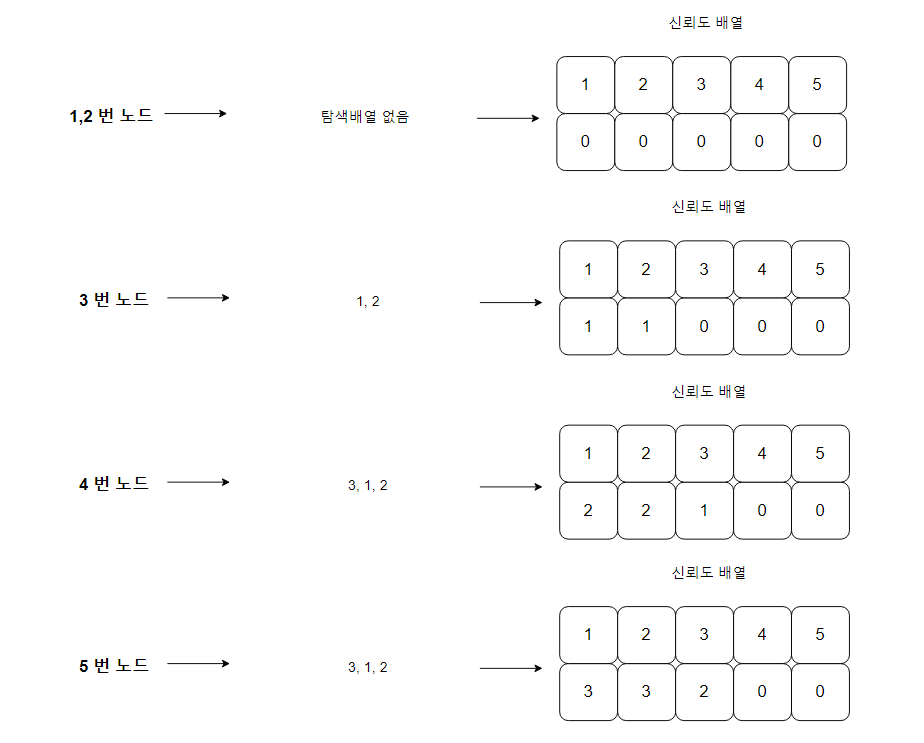
A가 B를 신뢰한다면 B를 해킹했을 때 A도 해킹이 가능하므로
4번이 3번을 신뢰하고, 3번은 1번, 2번을 신뢰하므로 1, 2번에 신뢰도를 더해줌.
5번도 3번을 신뢰하고, 3번은 1번 2번을 신뢰하므로 1, 2번에 신뢰도를 더해준다.

최종적으로 가장 신뢰를 많이 받은 컴퓨터를 해킹해야 가장 많은 컴퓨터를 해킹 할 수 있다.

예시에서의 답은 1, 2 이다.

코드

import java.util.*;

public class Main {
    static int n, m;	// 노드, 에지
    static boolean[] visit;		// 방문 배열
    static List<Integer>[] arr;		// 인접 리스트
    static int[] result;	// 신뢰도 배열
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        n = sc.nextInt();
        m = sc.nextInt();
        arr = new List[n + 1];
        result = new int[n + 1];
        visit = new boolean[n + 1];

        for (int i = 1; i <= n; i++) {
            arr[i] = new ArrayList<>();		// 인접 리스트 초기화
        }
        for (int i = 0; i < m; i++) {
            int s = sc.nextInt();	// 시작 노드
            int e = sc.nextInt();	// 종료 노드
            arr[s].add(e);
        }
        for (int i = 1; i <= n; i++) {
            visit = new boolean[n + 1];
            BFS(i);
        }
        int big = 0;
        for (int i = 1; i <= n; i++) {
            big = Math.max(big, result[i]);		// 최대값 탐색
        }
        for (int i = 1; i <= n; i++) {
            if (result[i] == big) {		// 최대값과 같다면 인덱스 출력
                System.out.print(i + " ");
            }
        }

    }
    public static void BFS(int n) {
        Queue<Integer> q = new LinkedList<>();
        q.add(n);
        visit[n] = true;
        while (!q.isEmpty()) {		// 큐가 비어있을 때까지
            int num = q.poll();
            for (int i : arr[num]) {
                if (visit[i] == false) {	// 방문하지 않은 노드가 나왔을 경우
                    result[i]++;
                    visit[i] = true;
                    q.add(i);
                }
            }
        }
    }
}