읽는데 5분정도 소요되는 글입니다. 감사합니다.
목차
1. 문제 설명
2. 접근 방법
3. 문제 풀이
1. 문제 설명
- Number of Digit One
Given an integer n, count the total number of digit 1 appearing in all non-negative integers less than or equal to n.
정수 n이 주어지는데, 음수 이외의 전체 숫자에서 1이 몇 번 출현하는지를 세는 문제입니다.
Example 1:
Input: n = 13
Output: 6
Example 2:
Input: n = 0
Output: 0
Constraints:
0 <= n <= 10^9
2. 접근 방법
문제를 보고, 처음에는 아래와 같은 방법으로 접근해보았습니다. 뭐라고 표현해야 할 지 모르겠지만, 분할 정복과 비슷한 느낌이었습니다.
0~9의 1의 자리 숫자를 계산할 때는 1보다 큰 수라면 count += 1합니다.
0~99의 10의 자리 숫자를 계산할 때는 10 ~ 19에서의 count += 10을 제외하고는 0~9의 1의 자리 숫자 계산이 x번 반복되므로 (count += 1) x을 해줍니다.
0~999의 100의 자리 숫자를 계산할 때는 100 ~ 199에서의 count += 100을 제외하고는 ((count += 10), (count += 1) x) * y) (여기서 x는 십의 자리 수, y는 백의 자리 수)를 해줍니다.
이런 식으로 문제의 작은 부분을 해결한 것을 조금 더 큰 부분에 적용하면서 문제를 해결하면 될 것 같다고 생각했습니다.
-> 비슷하지만 틀린 접근방법이었던 것 같습니다.
특정 케이스를 해결하기 위해서 너무 많이 덧붙여야 하는 문제가 발생했고 그 결과 코드만 보고 해당 알고리즘이라는 것을 쉽게 알기 힘들 정도가 되었습니다.
결국 풀지 못하고 스터디장님께 설명을 들었습니다.
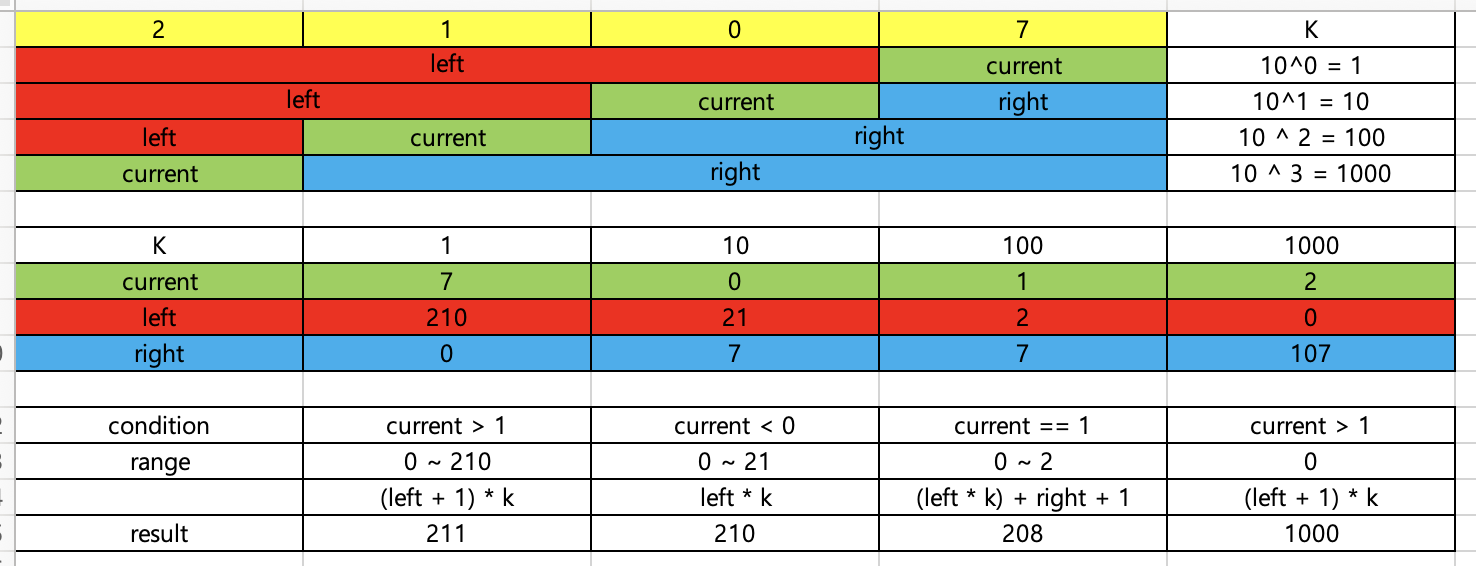
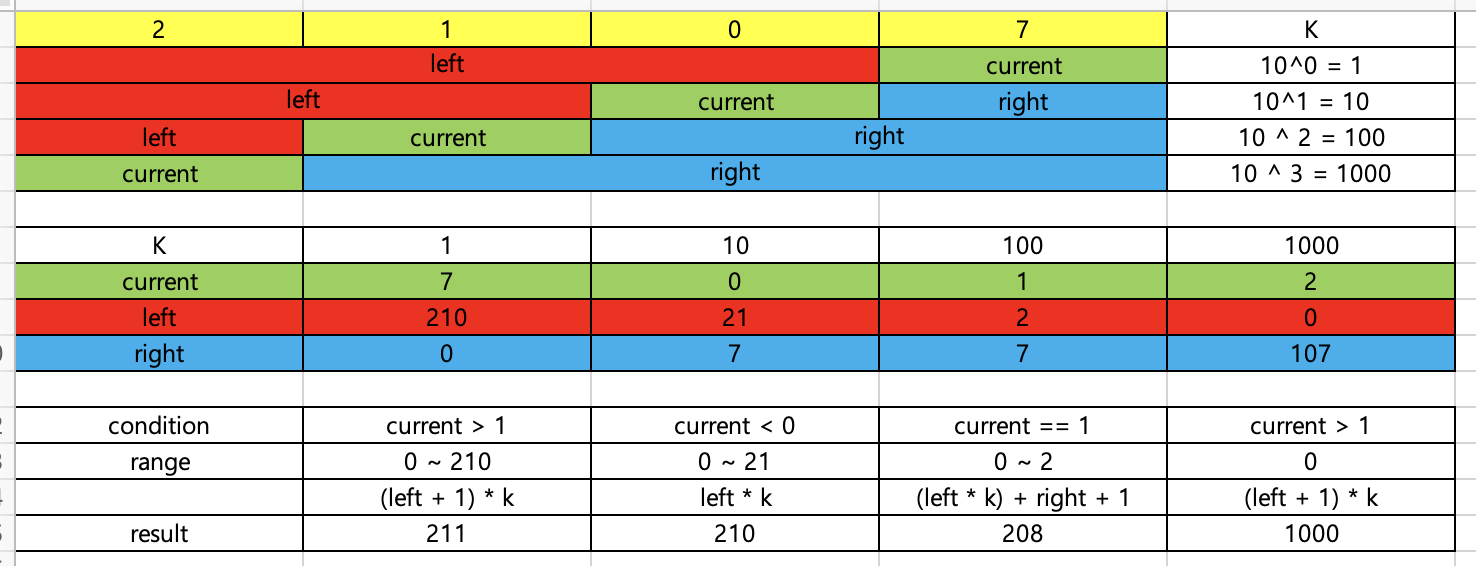
핵심은 한 자리씩 순회하며 현재 숫자가 1보다 큰지, 1인지, 1보다 작은지 보고 왼쪽의 숫자와 오른쪽의 숫자를 보고 1이 나올 개수를 판단하는 것이었습니다.
2107이라는 숫자를 예를 들어 설명드리겠습니다.
1의 자리에서는 1이 10을 순회할때마다 1번씩 나오므로 210번이 나오게 됩니다. 거기에다가 1의 자리 수가 1보다 크면 1이 추가되어, 총 211번이 나오게 됩니다.
만약 1의 자리 수가 1이었대도 right(0) + 1 로 1이 추가되고, 1의 자리 수가 0이라면 1이 추가되지 않아 210이 나오게 됩니다.
이런 식으로 10의 자리, 100의 자리, ... 반복하게되면 최종적으로 1이 몇 번 나오는지 결과를 얻을 수 있습니다.
3. 문제 풀이
class Solution:
def countDigitOne(self, n: int) -> int:
left = 1
result = 0
k = 1
while (left != 0) :
left = n // (k * 10)
right = n % k
current = (n // k) % 10
if (current > 1) :
result += (left + 1) * k
elif (current == 1) :
result += left * k + right + 1
else :
result += left * k
k *= 10
return result위 방식을 python 코드로 구현했습니다.
혹시 궁금하시거나 이해가 되지 않는 부분이 있으시다면 댓글이나 연락 부탁드리겠습니다. 감사합니다.