자료구조에 대한 알고리즘 공부를 하고서 여러 문제들을 풀고 DFS 문제들을 풀기전에 공부를 하려한다 ! 이름부터가 조금 무서워보인다. 그래도 한번 공부 해보았다 ! DFS에 대한 기본적인 개념과 코드를 통한 예시를 이번 포스팅에서 다루고 다음포스팅에서 BFS를 포스팅해보겠다 !!
DFS(깊이 우선 탐색)의 탐색 순서는 다음과 같이 동작한다. 쉽게 말해, 한 가지 길을 끝까지 파고들다가 막다른 길에 다다르면 되돌아와서 새로운 길을 다시 탐색하는 방식이다.
그림을 통해서 DFS를 쉽게 설명해보겠다 !
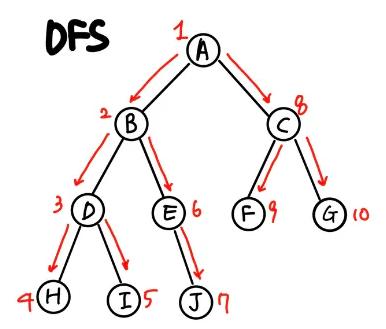
위에서 설명했듯이 DFS는 깊이 우선 탐색이다. 한가지 길을 끝까지 파고들고 막다른 길에 다다르면 다시 되돌아오는것이다. 그림을 설명해보겠다 !
- A에서 시작한다. 다시 한번 생각해보자 “깊이 우선 탐색”
- A의 자식노드 B를 탐색한다.
- B의 자식노드 D를 탐색한다.
- D의 자식노드 H를 탐색한다. 이후 막다른 길, 다시 D로 돌아간다.(백트래킹)
- D의 남은 자식노드 I를 탐색한다. 이후 막다른 길이고 전부 탐색했으니 B까지 올라간다.(백트래킹)
- B의 자식노드 E를 탐색한다.
- E의 자식노드 J를 탐색한다. 이후 막다른 길이고 전부 탐색했으니 A까지 올라간다.(백트래킹)
- A의 자식노드 C를 탐색한다.
- C의 자식노드 F를 탐색한다. 이후 막다른 길, 다시 C로 돌아간다.(백트래킹)
- C의 자식노드 G를 탐색한다. 이렇게해서 전부 탐색했다.
이렇게해서 탐색 순서를 그림으로 알아보았다. 하지만 여기서 주의할 점 ! ! !
** 탐색한 노드는 건너뛰고, 중복을 피하기위해 노드를 탐색할때마다 탐색 여부를 체크한다. **
이제 코드를 통해 알아보자 !!
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
// 입력을 빠르게 받기 위해 BufferedReader 사용
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 첫 줄에서 정점의 개수 N, 간선의 개수 M, 탐색을 시작할 정점 V를 입력받음
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken()); // 정점의 개수
int m = Integer.parseInt(st.nextToken()); // 간선의 개수
int start = Integer.parseInt(st.nextToken()); // 탐색을 시작할 정점 번호
// 인접 리스트를 초기화 (정점이 1번부터 시작하므로 n+1 크기로 생성)
ArrayList<Integer>[] graph = new ArrayList[n + 1];
for (int i = 1; i <= n; i++) {
graph[i] = new ArrayList<>();
}
// 방문 여부를 체크할 배열 (정점이 1번부터 시작하므로 n+1 크기로 생성)
boolean[] visited = new boolean[n + 1];
// 간선 정보를 입력받아 그래프를 구성 (양방향 간선)
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken()); // 간선의 시작 정점
int v = Integer.parseInt(st.nextToken()); // 간선의 끝 정점
graph[u].add(v);
graph[v].add(u);
// 예를들어 u = 4, v = 3 일때, 4번 노드와 3번노드는 양방향으로 연결돼있다.
// 따라서 실질적으로 노드와 간선을 그리는 부분이다.
}
// 각 정점의 인접 리스트를 정렬하여 방문 순서가 작은 번호부터 이루어지도록 설정
for (int i = 1; i <= n; i++) {
Collections.sort(graph[i]);
}
// DFS 탐색 결과를 저장할 StringBuilder
StringBuilder dfsResult = new StringBuilder();
// 스택을 사용하여 DFS 구현
Stack<Integer> stack = new Stack<>();
stack.push(start); // 시작 정점을 스택에 넣음
// DFS 탐색 시작
while (!stack.isEmpty()) {
// 스택의 최상단 노드를 꺼냄
int currentNode = stack.pop();
// 이미 방문한 노드라면 건너뜀
if (visited[currentNode]) {
continue;
}
// 현재 노드를 방문 처리하고 결과에 추가
visited[currentNode] = true;
dfsResult.append(currentNode).append(" ");
// 현재 노드의 인접한 노드들을 역순으로 스택에 추가
// 역순으로 추가하는 이유: 스택의 특성상 후입선출이므로 방문 순서가 작은 번호가 먼저 나오도록 하기 위해
List<Integer> neighbors = graph[currentNode];
for (int i = neighbors.size() - 1; i >= 0; i--) {
int neighbor = neighbors.get(i);
if (!visited[neighbor]) {
stack.push(neighbor);
}
}
}
// DFS 결과 출력
System.out.println(dfsResult.toString());
}
}이 코드를 통한 전체적인 플로우를 작성해보았다 !!
- 정점(N), 간선(M), 탐색 시작 정점(V)을 입력받는다.
- 그래프를 인접 리스트 형태로 초기화한다. (ArrayList 배열 생성)
- 방문 여부를 체크할
boolean배열을 초기화한다. - 간선 정보를 입력받아 그래프를 구성하고, 양방향 간선을 추가한다.
- 각 정점의 인접 리스트를 오름차순으로 정렬하여 방문 순서가 작은 번호부터 탐색하도록 설정한다.
- DFS 탐색 결과를 저장할
StringBuilder를 생성하고, DFS를 위한 스택을 초기화한다. - 시작 정점을 스택에 넣고, 스택이 비어있지 않을 동안 DFS 탐색을 진행한다.
- 스택의 최상단 노드를 꺼내어 현재 노드로 설정하고, 이미 방문한 노드라면 탐색을 건너뛴다.
- 현재 노드를 방문 처리하고, 탐색 결과에 추가한다.
- 현재 노드의 인접한 노드들을 역순으로 스택에 추가하여, 작은 번호의 인접 노드가 먼저 탐색되도록 한다.
- 스택이 빌 때까지 반복한 후, 탐색 결과를 출력한다.
그리고 스택으로 구현한 부분을 더 쉽게 재귀 호출을 통해 구현한 부분이다 !
// 노드를 그리는 부분까지 동일하기에 생략.
// DFS 탐색 결과를 저장할 StringBuilder
StringBuilder dfsResult = new StringBuilder();
// 재귀 방식으로 DFS 탐색을 시작
dfs(start, visited, graph, dfsResult);
// DFS 결과 출력
System.out.println(dfsResult.toString());
}
// DFS 메서드: 재귀적으로 DFS를 수행
public static void dfs(int node, boolean[] visited, ArrayList<Integer>[] graph, StringBuilder dfsResult) {
// 현재 노드를 방문 처리하고 결과에 추가
visited[node] = true;
dfsResult.append(node).append(" ");
// 현재 노드의 인접한 노드들을 탐색 (오름차순 정렬된 인접 노드들)
for (int neighbor : graph[node]) {
if (!visited[neighbor]) { // 방문하지 않은 노드만 재귀적으로 방문
dfs(neighbor, visited, graph, dfsResult);
}
}
}
}보통은 이렇게 재귀 호출을 통해 더 간단하게 푼다 !!
