Prim Algorithm

최소 신장 트리

그래프가 주어졌을 때, 노드(node)들을 모두 연결하고 싶다고 하자. 노드들을 모두 가지고 있고, 엣지(edge)가 가장 적은 그래프를 신장 트리(Spanning Tree)라고 한다. 여기서 엣지에 가중치(cost)가 있고, 가중치가 가장 적은 신장 트리를 최소 신장 트리(Minimum Spanning Tree)라고 한다. 이 때 사이클(Cycle)이 없어야한다.

• 노드가 N개이다.
• 엣지가 N-1개이다.
• 사이클이 없다.(사실 노드가 N개고 N-1개의 엣지가 모두 연결하려면 사이클이 있으면 안된다.)
• 가중치가 최소이다.

Prim Algorithm

1. 하나의 노드를 가진 트리에서 시작한다(아무 노드나)
2. 트리에 인접한 엣지들 중 가장 작은 가중치를 가진 엣지를 추가한다. 이때, 사이클이 만들어지면 안된다.
3. 최소 신장 트리가 될 때까지 반복한다.

Algorithm Prim(G, T)

• T <- Empty Set
• U <- {1}
• While U != V do
  • U의 한 노드와 V-U의 한 노드를 잇는 엣지들 중 웨이트가 제일 작은 것
  • uv를 T에 추가
  • V를 U에 추가

Example

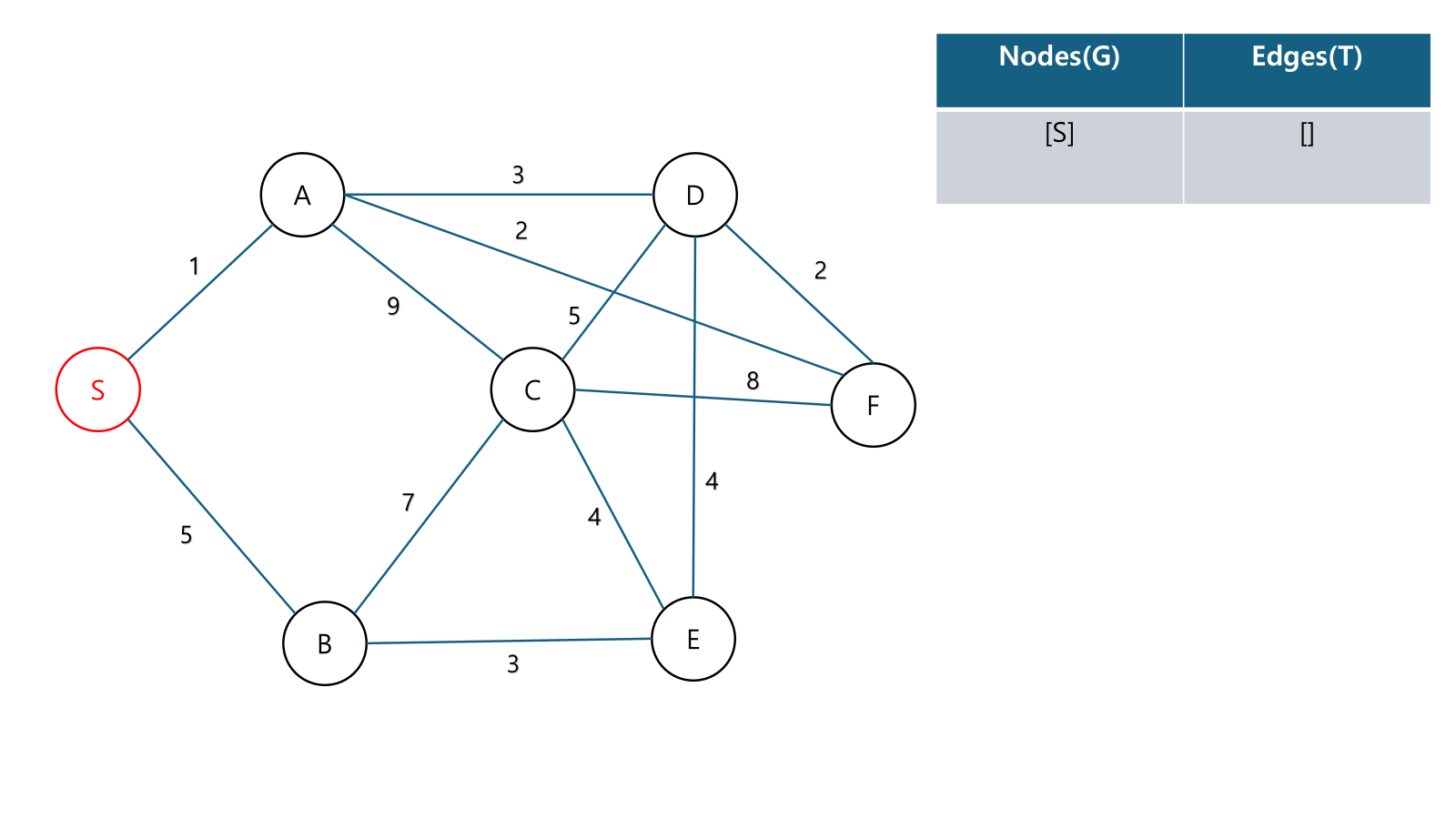
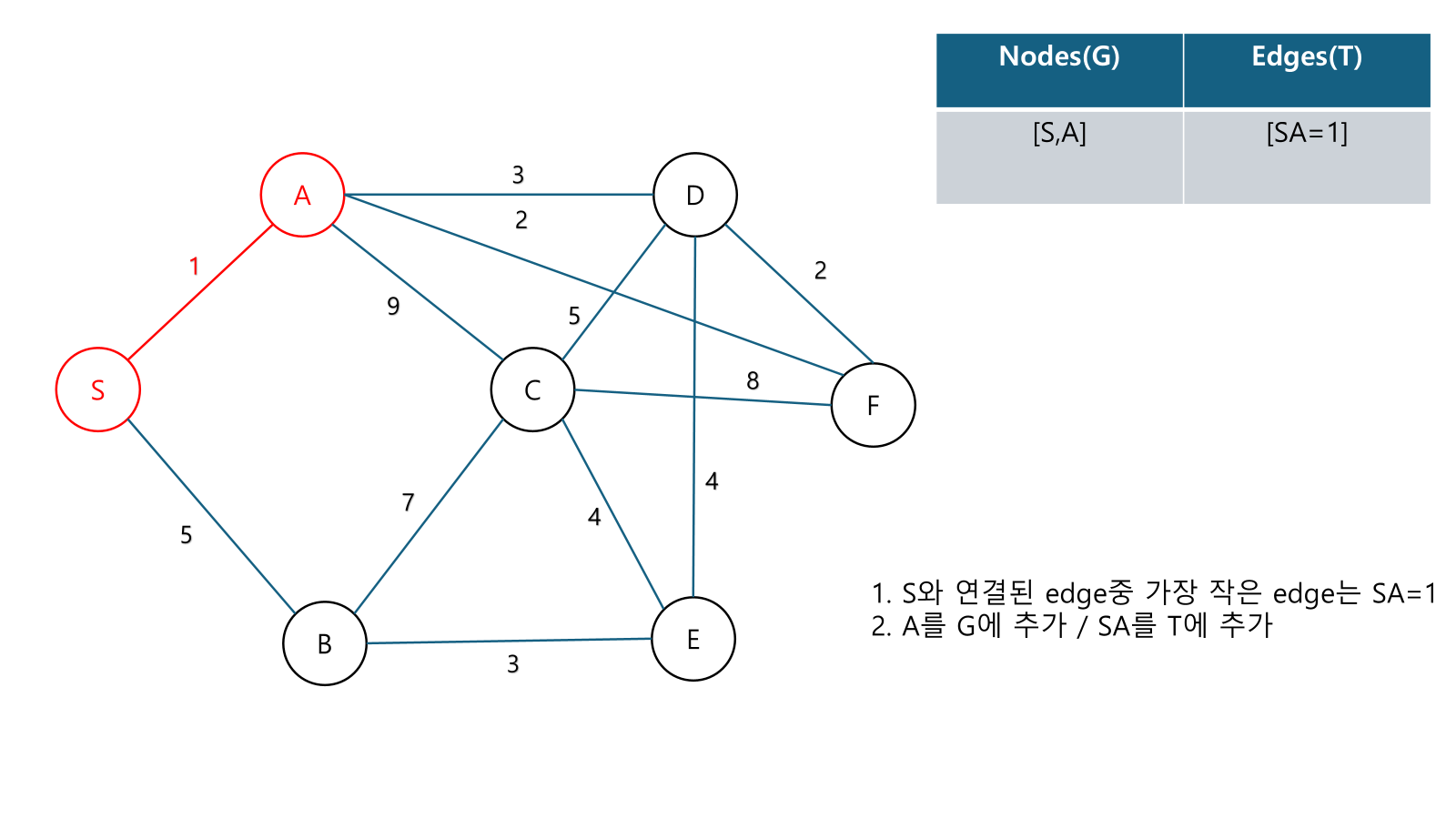
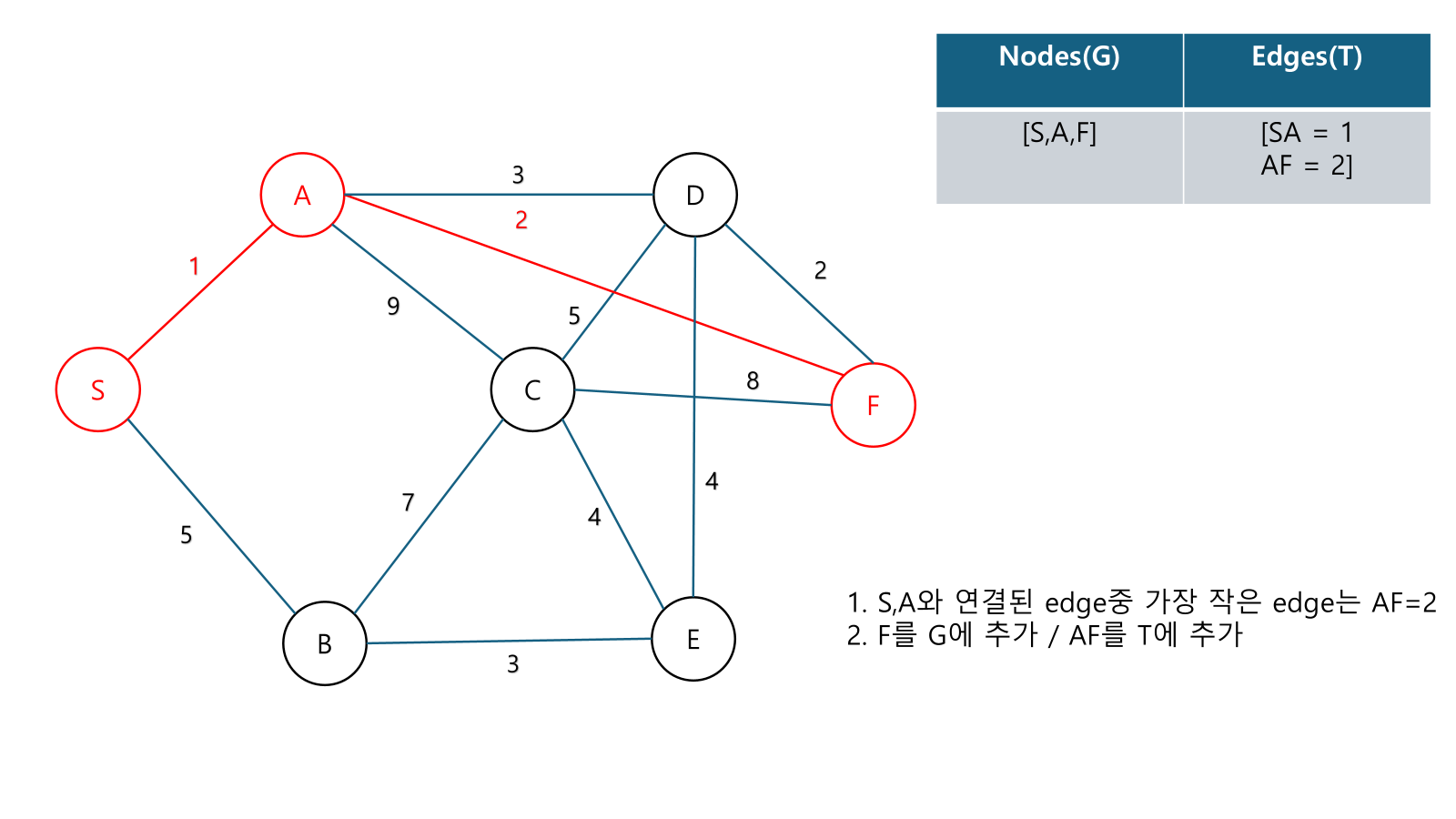
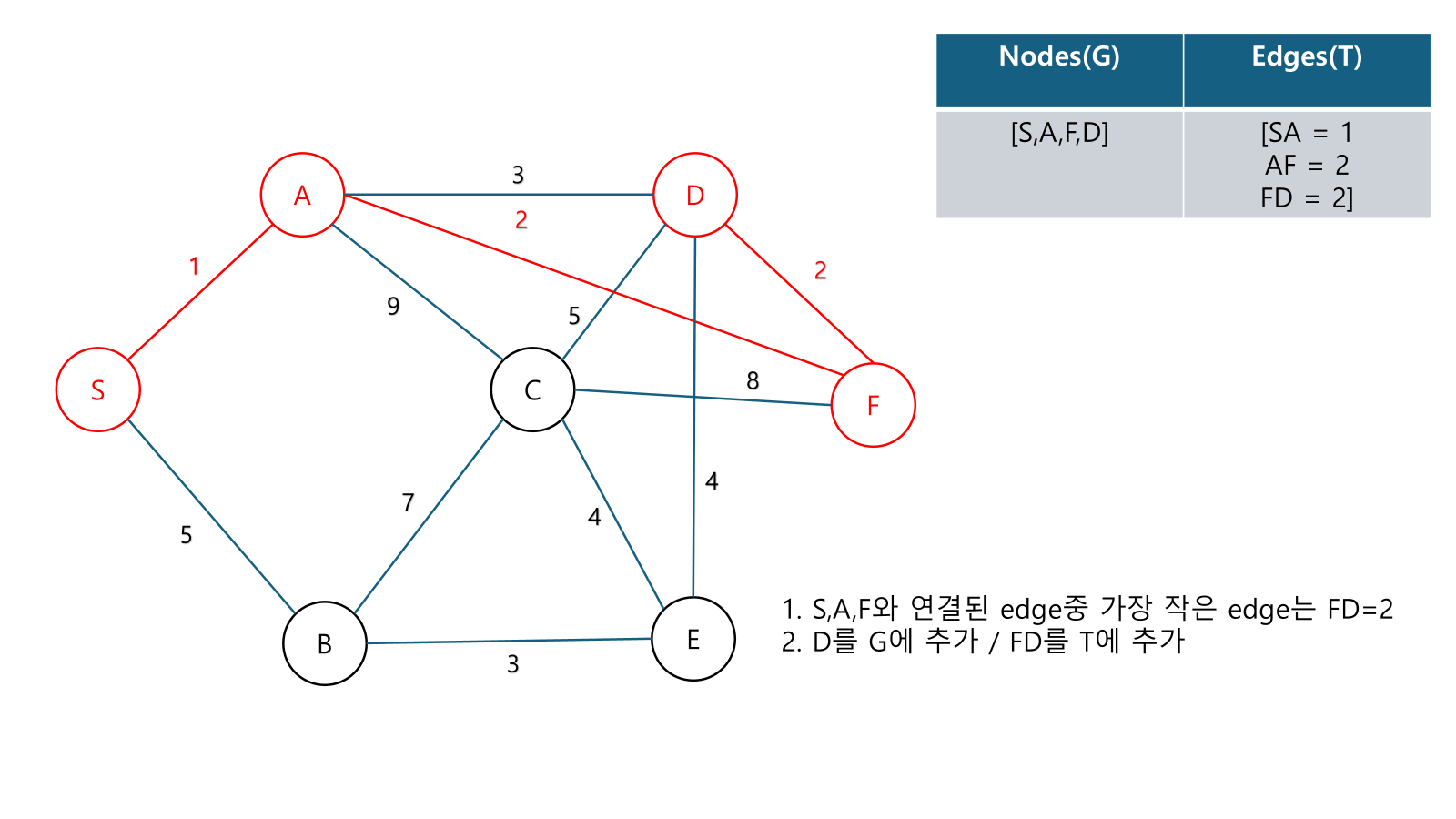
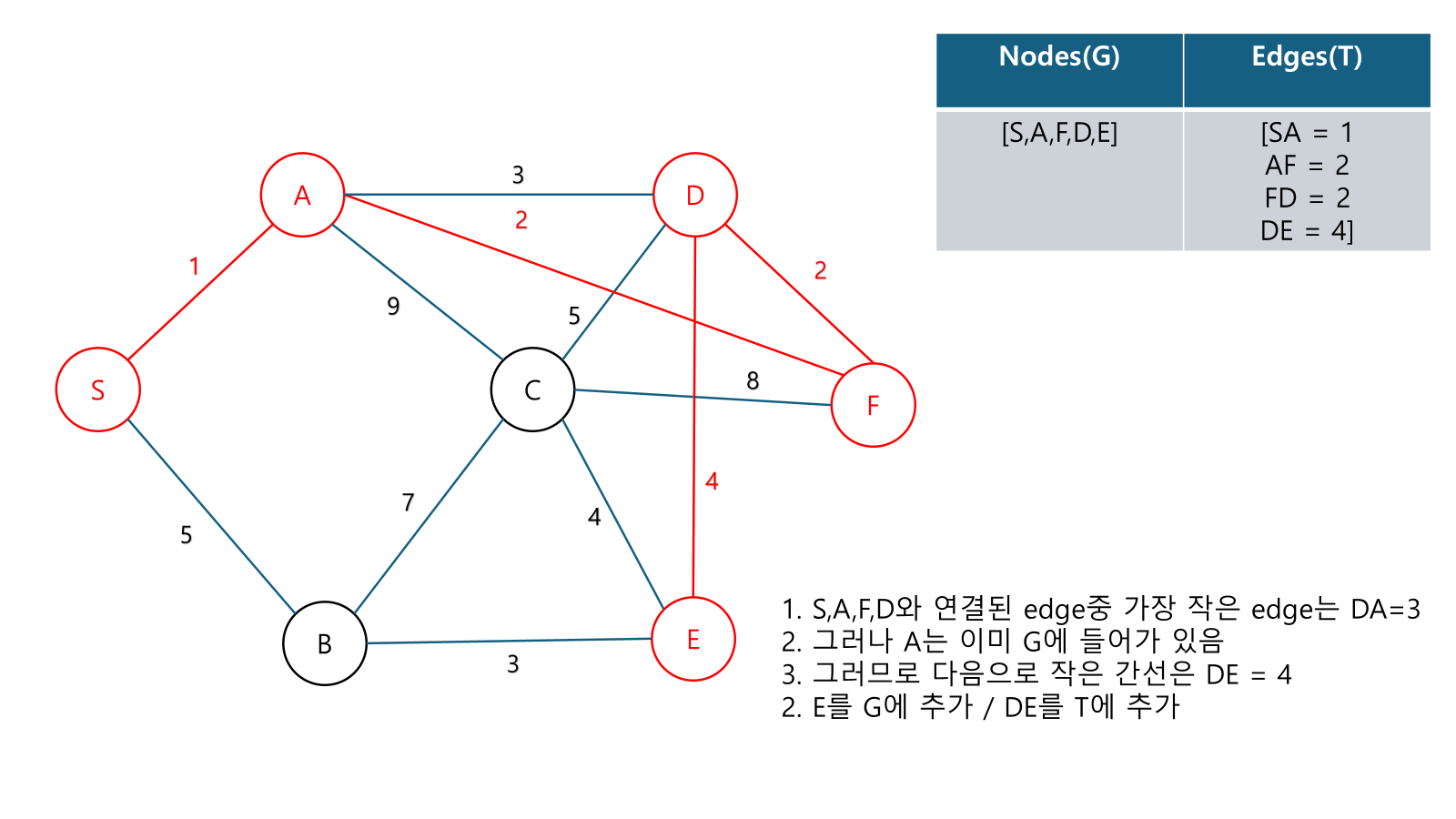
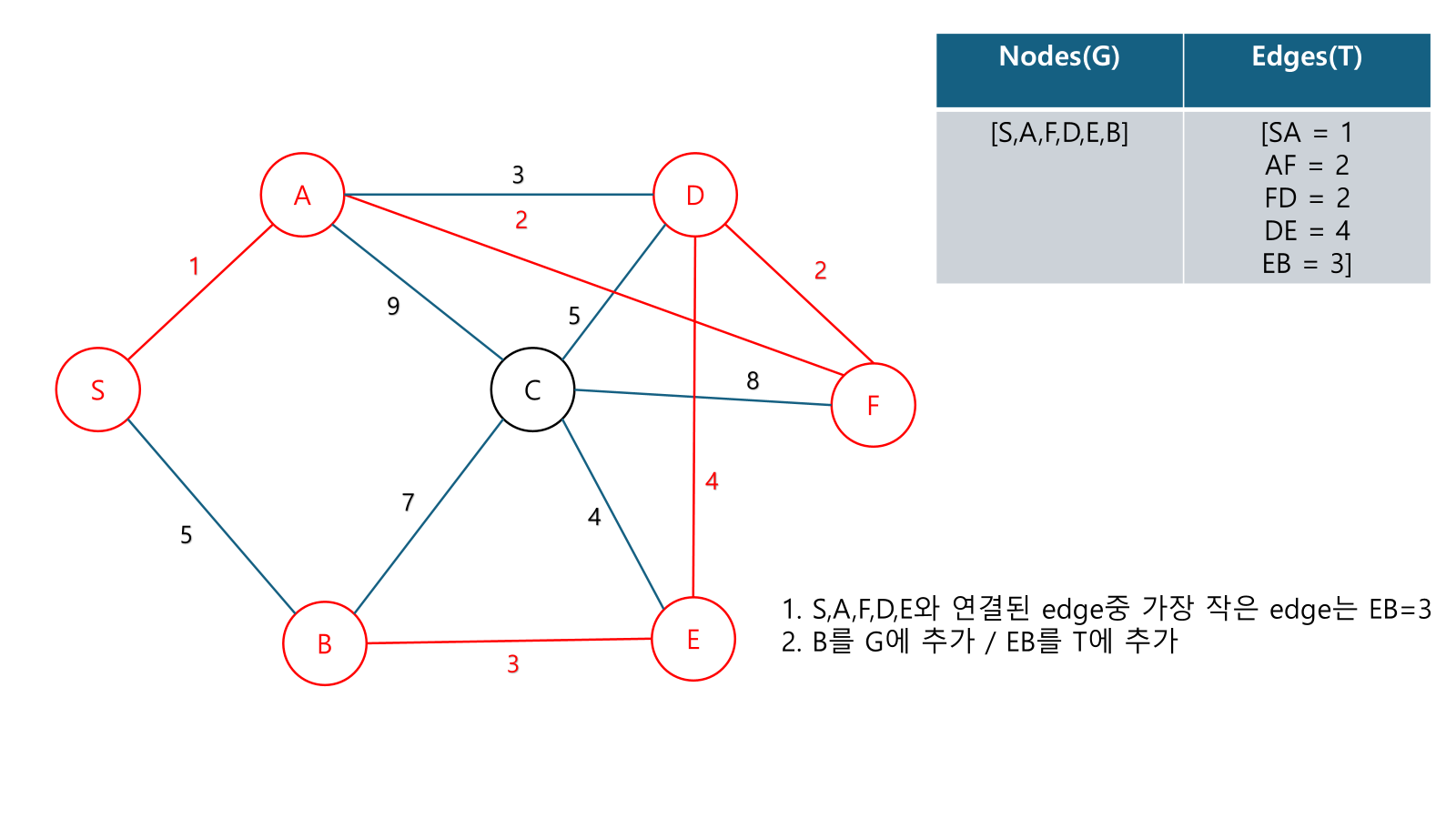
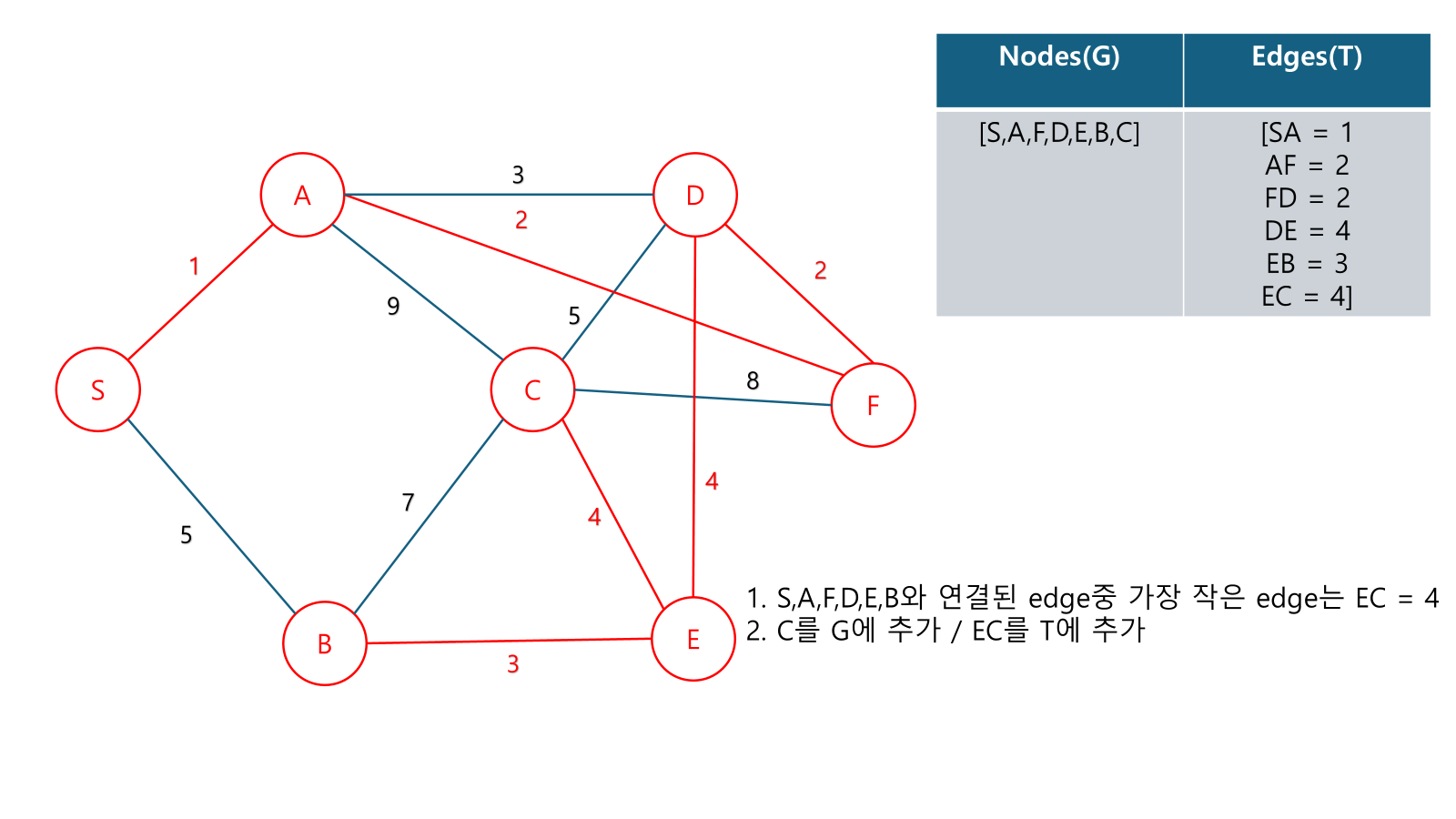
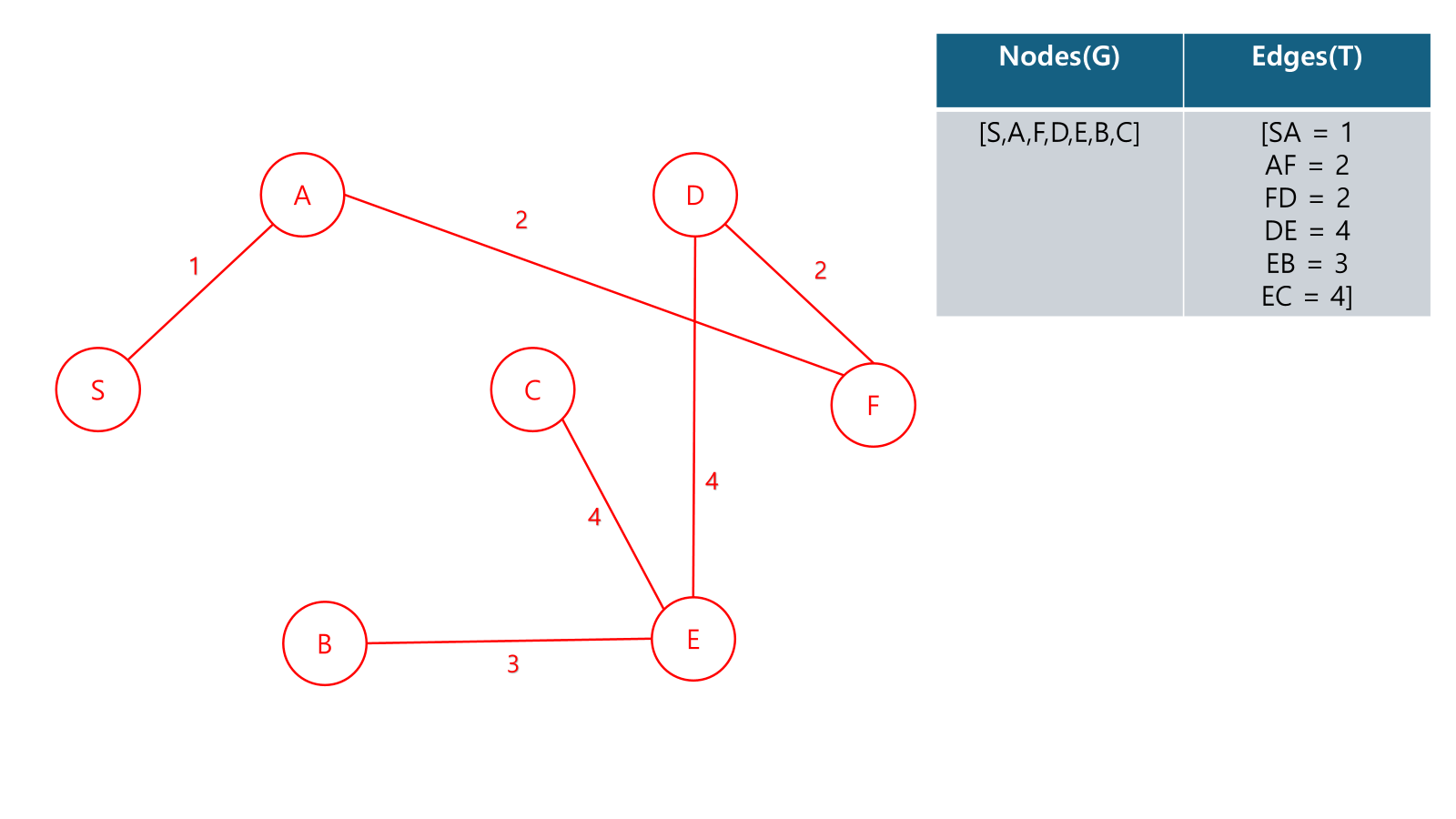
성능 : $O(MlogN)$
$N$개의 노드가 있고, $M$개의 간선이 있을 때
우선순위 큐를 이용한다.
1. 간선들을 저장한다. $O(M)$
2. 맨 처음 노드를 추가했다 표시하고 노드의 인접 간선들부터 우선순위 큐에 넣는다.
3. 맨 위에 있는 간선을 꺼내 노드가 모두 포함된 간선인지 확인한다
3-1. 만약 노드가 모두 포함되었으면 그냥 진행한다.
3-2. 만약 노드가 포함되어있지 않으면 노드를 추가했다 표시하고 노드에 있는 간선들을 우선순위 큐에 넣는다.
4. 우선순위 큐가 비어있지 않으면 3으로 돌아간다. 비어있으면 종료한다.

2,3,4번 과정을 거치면 결국 모든 노드에 대한 간선들이 우선순위 큐에 들어가야 한다.
모든 간선에 대해 인접 간선을 넣는데 소요되는 시간복잡도는 $O(M)$이며, 힙에 넣고 정렬하는 과정이 $O(logN)$이 걸린다. 그러므로 힙 구성은 $O(MlogN)$이 걸린다.
노드에 대한 최솟값을 가져오는 시간복잡도는 $O(logN)$이며, 모든 정점을 대상으로 하므로 $O(N)$만큼 걸린다. 그러므로 힙에서 가져와서 MST를 구성하는데 걸리는 시간은 $O(NlogN)$이 걸린다.

최종 시간복잡도는 $O(MlogN + NlogN)$이고 대부분의 경우 $M$이 $N$보다 크기 때문에 $O(MlogN)$이 걸린다.

사이클이 생겼을 때

$T_{mst}$에 간선 e를 넣었더니 사이클이 생겼다고 해보자. 간선을 연결 하기 전의 트리에 들어있는 노드와 연결하려는 트리에 들어있지 않은 노드가 존재한다. 사이클을 만드는 간선 중 가장 가중치가 큰 기존에 트리에 있던 e' 또한 존재한다.

• w(e)와 w(e')를 비교해보자. w(e) < w(e')면 e'를 빼면 된다. 사이클이였기 때문에 여전히 트리가 유지됨.
• w(e) > w(e')면, 우리 알고리즘은 가장 작은 가중치를 가진 엣지를 추가하므로, 오류가 생김. 결국 우리 알고리즘을 돌린 게 아니라는 소리.
  그러므로 간선 e를 넣었을 때 사이클이 생기는 경우는 가장 가중치가 큰 e'를 버리면 된다.
• w(e) == w(e')면, e와 e'중 아무거나 넣어도 상관없다.