숫자 체계

숫자 체계

숫자 체계는 2개로 구성되어있다.

• Base or Radix value : 진수를 의미하며, 값에 따라서 진수가 달라진다. 10진수, 2진수 등
• Set of coefficients : 한 digit안에 들어가는 숫자의 집합을 의미한다.

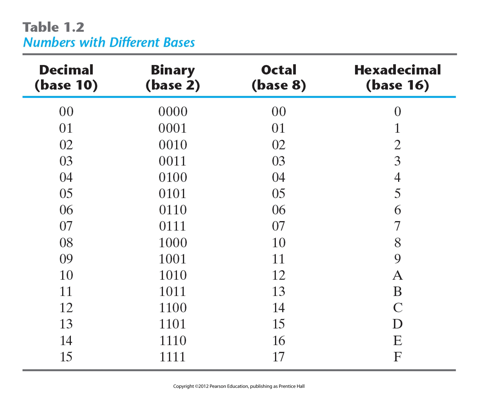
우리는 일상생활에서 10진수 체계를 사용한다. 10진수는 아래와 같이 정의할 수 있다.

• Base : 10
• Set of coefficients : {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
• $(2357)_{10}$진수 체계 : $2 * 10^3 + 3 * 10^2 + 5 * 10^1 + 7 * 10^0$

2진수 체계

• Base : 2
• Set of coefficients : {0, 1}

8진수 체계

• Base : 8
• Set of coefficients : {0, 1, 2, 3, 4, 5, 6, 7}

16진수 체계

• Base : 16
• Set of coefficients : {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f}

Base-r System

위와 같은 규칙들을 통해 우리는 숫자 체계를 일반화 할 수 있다.

r진수 체계는

• Base : r
• Set of coefficients : {0, 1, 2, ... , r-1}

---

이진 숫자

비트(bit)는 앞에서 말한 것처럼 이진 자릿수를 의미함. 이런 bit가 8개 합쳐진 것을 byte라고 부르며, N개의 비트는 0부터 2^N-1까지 나타낼 수 있음. 우리가 흔히 1000bit == 10^3bit == 1KB로 알고 있는데, 실제로는 2^10bit == 1024bit == 1KB이기 때문에, 저장장치의 용량을 볼 때 실제와 차이가 나는 경우가 종종 있음.

• 2^10bit = 1KB
• 2^20bit = 1MB
• 2^30bit = 1GB
• 2^40bit = 1TB

---

이진수 체계에서의 숫자 연산

더하기

더하기는 간단하다. 이진수 체계에서 더하기는 carry와 sum을 가지는데, carry는 다음으로 넘기는 숫자를 의미하고, sum은 결과를 의미한다.

A	B	CARRY	A+B
0	0	0 carry	0
0	1	0 carry	1
1	0	0 carry	1
1	1	1 carry	0

빼기

빼기 또한 간단하다. 이진수 체계에서 더하기는 borrow와 difference를 가지는데, borrow는 부족하여 빌려오는 숫자를 의미하고, difference는 결과를 의미한다.

A	B	BORROW	A-B
0	0	0 borrow	0
0	1	1 borrow	1
1	0	0 borrow	1
1	1	0 borrow	0

곱하기

곱하기는 자릿수마다 곱하면 된다.

   1011
   X101
  ㅡㅡㅡ
   1011
  0000
 1011
 110111

---

10진수의 n진수 변환

• 일반적으로 숫자는 정수 부분과 소수 부분을 구분해주는 radix point라는 게 존재하고, radix point 앞은 정수, 뒤는 소수로 구분된다.(소수점 윗자리, 소수점 아래자리)
• 정수 부분은 계속해서 n으로 나눔으로써 정수 부분을 변환할 수 있다.
• 소수 부분은 계속해서 n으로 곱함으로써 소수 부분을 변환할 수 있다.

41을 2진수로 변환해보자
41/2 = 20 ... 1 -> a0 = 1
20/2 = 10 ... 0 -> a1 = 0
10/2 = 5 ... 0 -> a2 = 0
5/2 = 2 ... 1 -> a3 = 1
2/2 = 1 ... 0 -> a4 = 0
1/2 = 0 ... 1 -> a5 = 1
a5a4a3a2a1a0 = 101001

153을 8진수로 변환해보자
153/8 = 19 ... 1 -> a0 = 1
19/8 = 2 ... 3 -> a1 = 3
2/8 = 0 ... 2 -> a2 = 2
a2a1a0 = 231

0.6875를 2진수로 변환해보자
0.6875*2 = 1 + 0.375 -> a1 = 1
0.375*2 = 0 + 0.750 -> a2 = 0
0.75*2 = 1 + 0.5 -> a3 = 1
0.5*2 = 1 + 0.0 -> a4 = 1
a1a2a3a4 = 0.1011

---

2^n진수끼리의 변환

• 2^n진수끼리의 변환은 radix point로부터 특정 자릿수들을 하나로 묶음으로 편하게 변환할 수 있다.
• 2 -> 8진수는 3자리씩 묶어서 나타내면 된다.
• 8 -> 2진수는 한자리를 3자리로 풀어서 나타내면 된다.

2진수 101011.101을 8진수로 변환해보자
(101 011).(101)
5 3 . 5 = 53.5

2진수 11110100101011.10100110을 16진수로 변환해보자
(11 1101 0010 1011).(1010 0110)
3 D 2 B . A 6 = 3D2B.A6

---

MSB와 LSB

• MSB : Most Significant Bit의 약자로 제일 앞에 있는 비트를 말한다. 데이터 통신에서 가장 큰 차이를 내기 때문에 데이터에 영향을 제일 많이 준다.
• LSB : Less Significant Bit의 약자로 제일 뒤에 있는 비트를 말한다. 데이터 통신에서 가장 작은 차이를 내기 때문에 데이터에 영향을 제일 적게 준다.

100111에서 맨 앞의 1은 2^5값을 가지기 때문에 맨 뒤의 2^0값을 가지는 1과는 큰 차이가 난다.