[LeetCode/Top Interview 150] [Binary Search Tree (BST)] 230. Kth Smallest Element in a BST

문제 링크: https://leetcode.com/problems/kth-smallest-element-in-a-bst/?envType=study-plan-v2&envId=top-interview-150
사용 언어: Java(OpenJDK 17. Java 8)

난이도: medium

문제:

Given the root of a binary search tree, and an integer k, return the kth smallest value (1-indexed) of all the values of the nodes in the tree.

Example 1:

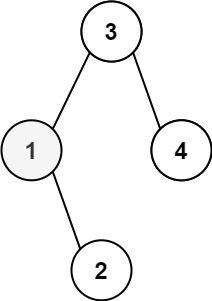
Input: root = [3,1,4,null,2], k = 1
Output: 1

Example 2:

Input: root = [5,3,6,2,4,null,null,1], k = 3
Output: 3

Constraints:

The number of nodes in the tree is n.
1 <= k <= n <= 10^4
0 <= Node.val <= 10^4

Follow up: If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize?

전략:

전체 트리의 값 중에서 k 번째(1번부터 시작)로 작은 값을 구하는 문제.
중위탐색으로 작은 값부터 순회하며 cnt 변수로 체크하다가 cnt == k가 되는 순간 리턴

추가: 만약 BST가 자주 수정되고, k번째로 작은 요소를 자주 찾아야 한다면, 어떻게 최적화 할 것인가?

코드 구현:

class Solution {
    int cnt=0;
    int kcnt;
    int answer;
    public int kthSmallest(TreeNode root, int k) {
        kcnt = k;
        inOrder(root);
        return answer;
    }

    public void inOrder(TreeNode node) {
        if (node == null || cnt > kcnt) { return; }
        inOrder(node.left);
        cnt++;
        if (cnt==kcnt) { answer=node.val; return; }
        inOrder(node.right);
    }
}
Time: 0 ms (100%), Space: 43.42MB (99.63%) - LeetHub

실행결과:
https://github.com/1-vL/LeetCode/blob/main/0230-kth-smallest-element-in-a-bst/0230-kth-smallest-element-in-a-bst.java

개선 방안:

수정이 빈번한 경우, 새로 추가된 값이 k번째인지 계산이 꾸준히 필요하다면?
조건에 따라 여러가지 방법이 있을 것이다. 트리 구조를 전체적으로 변경할 수 있다면 균형잡힌 트리가 되도록 하고, k 값이 고정되어 있다면, 최초에 k번째로 작은 값을 구해서 저장하고, 그 값을 기준으로 삽입 및 수정이 발생하는 경우 더 작은 값이 생기거나 없어지는 경우에만 다시 k번째로 작은 요소를 찾는 탐색을 하고, 그렇지 않은 경우 기존 k 값을 리턴할 것이다.

Solutions 탭의 타인 코드:

class Solution {
    public static int ans = 0;
    public int kthSmallest(TreeNode root, int k) {
        helper(root, k);
        return ans;
    }

    public int helper(TreeNode root, int k) {
        if (root == null) {
            return 0;
        }
        int leftCount = helper(root.left, k); // k번째 요소 탐색
        int rightCount = helper(root.right, k - leftCount - 1); // 왼쪽 하위노드에서 체크한 수 만큼 제외한 k - leftCount - 1번째 요소 탐색
        if (k == leftCount + 1) { // 정답 찾음(1인덱스)
            ans = root.val;
        }
        return leftCount + rightCount + 1; // 좌우 노드의 체크한 요소들 갯수의 합
    }
}
Time: 0 ms (100%), Space: 43.66MB (96.51%) - LeetHub

회고:

직전에 풀었던 유형에서 크게 변하지 않아서 정말 쉬웠다.
다만 k번째 요소를 더 자주 탐색하는 경우에 대한 추가 생각 부분에서는 실제 테스트를 해 볼만한 환경은 아니어서 조금 아쉬웠다.