오늘 SSAFY 공지 채널에 아래의 글이 올라왔다.


참여해보고 싶은데 마감일이 이번달이다..
심지어 회사가 참여할 수 있는게 아닌가..?? 싶은데
오늘 일과를 마무리하고 다시 봐야겠음
💫 오늘의 목표
오늘은 15:20에 병원 예약이 있어서 조퇴 예정임
그 전까지 진도를 많이 빼놔야지

PS 2문제 이상 풀기
오늘도 기출문제 모음에서 풀어보려고 한다.
1) 주사위 고르기
아 계속 논리가 꼬인다..
아래 흐름처럼 정리는 했는데, 어느 부분을 같이 실행할 수 있고 못할지에 대해서 결정하는게 어려웠다.
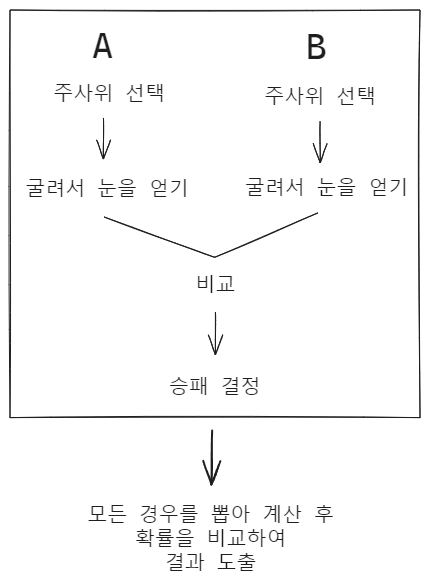
| 분류 | 방법 | 결과값 |
|---|---|---|
| 주사위 선택 | 조합 | A : 1,4 1, 4번 주사위 선택 |
| 숫자 얻기 | 순열 | [1,2], [1,3], [1,4] ... 1번 주사위에서 숫자 1을, 4번 주사위에서 각 2,3,4 숫자를 뽑음 |
| 비교 | 순열 | 승 : 596, 무 : 196, 패 : 504 A에서 얻은 숫자들과 B에서 얻은 숫자들을 비교 |
| 승패결정 | 단순계산 | 승리한 수가 가장 많은 경우를 return |
구현을 어떻게 해야할지 모르겠어서 다른 사람들의 접근법을 보았는데
조합 + 브루트포스 + 이진탐색을 활용하는 문제라고 한다..?
왜 이진탐색을 해야할까
- 주사위는 10개 이내
- 주사위의 눈은 6개
- 눈의 수는 100 이하
위 조건들을 가지고 대입해보자
메인로직 : A와 B가 주사위를 선택하고 숫자를 얻고 이를 각각 합하여 비교를 통해 결과를 합산한다.
| 분류 | 방법 | 결과값 | 시간복잡도 |
|---|---|---|---|
| 주사위 선택 | 조합 | A : 1,4 1, 4번 주사위 선택 | O(10C5) |
| 숫자 얻기 | 순열 | [1,2], [1,3], [1,4] ... 1번 주사위에서 숫자 1을, 4번 주사위에서 각 2,3,4 숫자를 뽑음 | O(6^5 * 6^5) |
| 비교 | 순열 | 승 : 596, 무 : 196, 패 : 504 A에서 얻은 숫자들과 B에서 얻은 숫자들을 비교 | 구했다는 전제로 O(1) |
| 승패결정 | 단순계산 | 승리한 수가 가장 많은 경우를 return | O(1) |
추가조건) A가 주사위를 고르면 나머지 주사위는 B것이 된다.
=> 10C5 x 6^5 x 6^5 = 15237476352 = 1.~ ×10^10
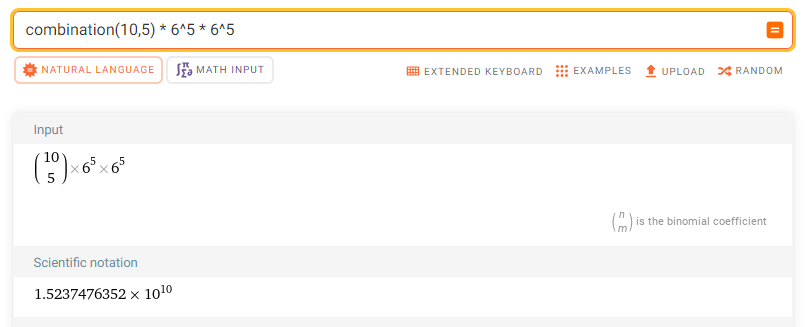
100억 이상이므로 불가능하다.
그러면 어느 경우에서 줄일 수 있을까
메인로직을 다시 가져와서 분해해보자.
메인로직 : A와 B가 주사위를 선택하고 숫자를 얻고 이를 각각 합하여 비교를 통해 결과를 합산한다.
1) 주사위를 선택하는 부분에서 줄일까?
모든 경우를 봐야 알 수 있으므로 줄일 수 없다.
2) 주사위를 얻은 뒤 각 눈을 얻는 경우에서 줄일까?
이 상황에선 가장 유력하지만..
그러면 모든 경우를 합산할 수 없다.
어디일까.. 줄일 수 있는 부분이..
합산하지 않아도 높은 확률임을 보일 수 있나?
아으.. 생각이 잘 안된다
2024 카카오 겨울 인턴십 코딩테스트 문제해설 을 결국 참고해서 아이디어를 얻기로 했다.
시간복잡도를 줄이기 위해 A와 B의 주사위를 한꺼번에 모두 시뮬레이션해 승패를 판단하는 대신, A와 B의 주사위를 따로 시뮬레이션하는 아이디어가 필요합니다.따로 시뮬레이션 한다..?
아 그건가
시간복잡도 전략 #1
곱하기를더하기로 바꿀 수 있어야한다.
이게 보통 전략인데
그러면 A를 굴려서(6^5) 모든 경우의 수를 저장하고, B도 굴려서(6^5) 모든 경우를 저장한다.
그리고?
...
아아아아 알 것 같다!
우선 A가 가질 수 있는 모든 조합의 합과 B가 가질 수 있는 모든 조합의 합을 가졌다고 생각해보자.
A : 1,1,1,2,3,4,5,6,7
B : 1,1,1,1,1,6,7,8,11
여기서 A만 이분탐색을 통해 이기는 경우를 저장하면 된다!
idx가 0~2일 때 A[idx]는 1이다.
B에 이분탐색을 해서 1보다 작은 경우를 찾으면 없으므로 0
idx가 3일 때 A[3]은 2이다.
B에 이분탐색을 해서 2보다 작은 경우를 찾으면 인덱스 4까지 이므로 5를 더한다
idx가 4일 때 A[4]은 3이다.
B에 이분탐색을 해서 3보다 작은 경우를 찾으면 인덱스 4까지 이므로 5를 더한다
이렇게 반복하면 모든 이기는 경우의 수를 구할 수 있음!
이걸 의도한 문제인지 확인하기 위해 다시 해설을 보니 맞았음!
그런데 꼭 이분탐색이 아니라 누적 합, 투 포인터 등의 기법으로도 가능하구나
[PCCP 기출문제] 1번 / 붕대 감기
로직은 다 맞는데 왜 하나가 틀렸을까
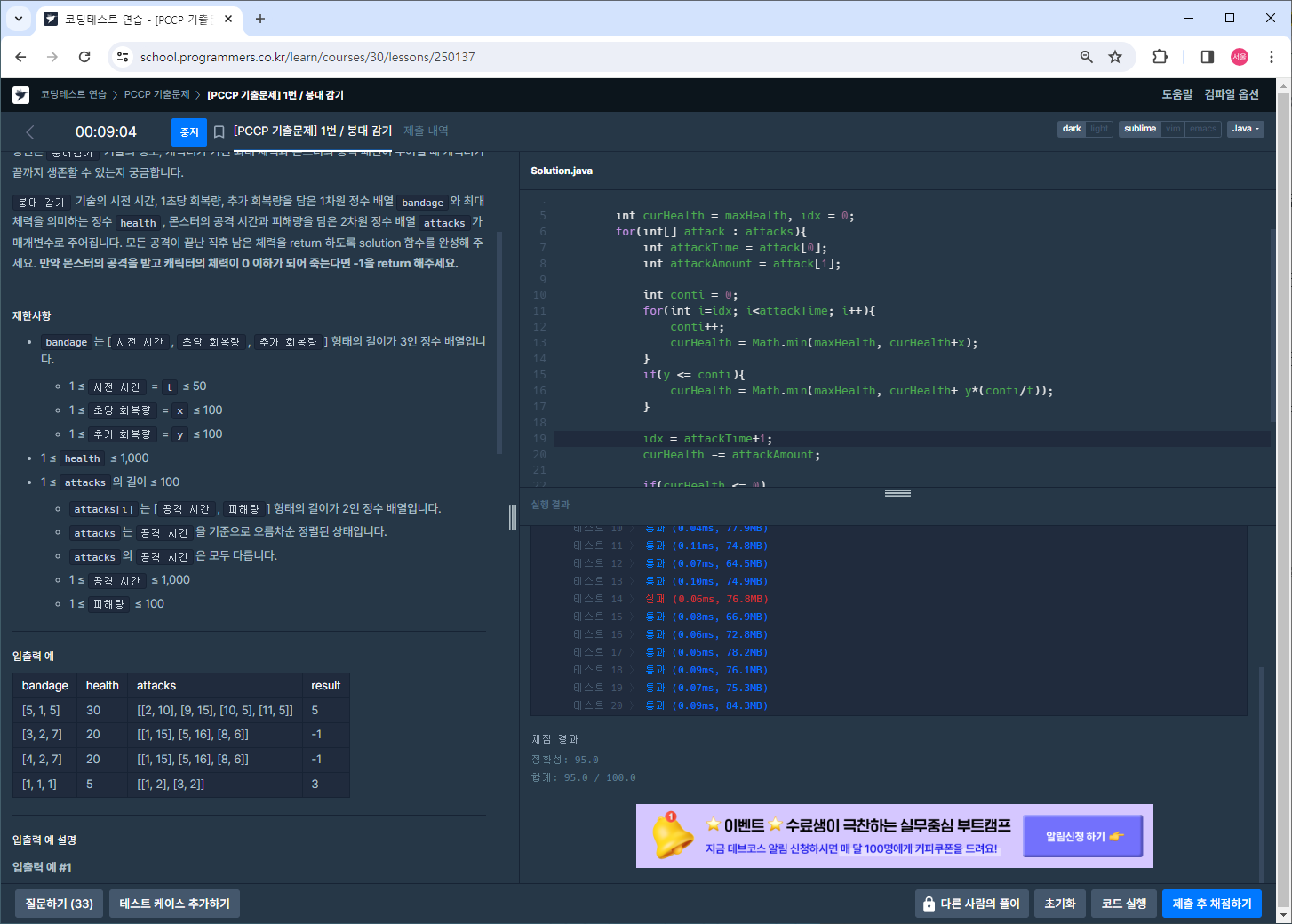
그렇게 한참 고민을 했는데
맞췄음..
틀렸던 이유는
연속 시간(conti)과 시전시간(t)로 비교해서 추가 회복량을 추가해야 했는데.. 변수를 잘못 넣었음
오늘의 코드 기록