오늘의 플래너
요새 집에만 가면 플래너를 펼치질 못하고 있다. 이걸 어떻게 해결할지 고민하다가 처음 플래너에 사용에 익숙해지기 위해 스티커로 꾸몄으니 앞으로도 집에서 모든 활동을 끝낸 뒤에 스티커를 붙인다면 좀 더 손에 붙지 않을까라는 생각이 들었다.
앞으로 꾸미는 건 집에 있는 나에게 맡겨야지.

그리고 하나 더 평소와 다르게 해볼 것은 목차에 depth를 추가하는 것.
단순히 1,2,3... 배열은 아 오늘 몇개 했네 정도의 생각만 들어서 다 부숴보자 하고 시작하더라도 큰 목표의식이 들지 않았다.
왜일까 생각하다가 이 각각의 목표가 너무 독립적이라 했으면 ok 흐름으로 흘러가서 그럴 수도 있겠다고 생각했음.
그래서 오늘부터 목차에 depth를 추가함으로서 앞의 목표를 끝내야 올 수 있는 단계임을 나타내고자 했다.
좀 더 많이 달성할 수 있길 바라며, 오늘 하루도 알차게 갓생을 살아보쟈
depth 1) PCCP 대비 2문제 이상 풀기
문제 1) 등굣길
많이 풀어본 유형의 문제였다.
가로와 세로가 100 길이 이하이므로 맵의 크기는 최대 1만이다.
모든 칸에 대해서 오른쪽과 아래로 이동 가능하므로 한칸 당 2번의 이동 결과가 발생할 수 있다. 그러면 간단하게만 생각해봐도 2^10000 이므로 엄청난 시간복잡도를 가짐을 확인 가능하다.
또한, 이 문제가 동적 계획법 문제임을 가장 빠르게 확인하려면 특정 수로 나눈 나머지를 구해야 한다는 조건이 있는지 살펴보는 것이 좋다. 그리고 이런 유형을 많이 풀었다면, 왔던 길을 되돌아가는 경우가 없으므로 dp로 구할 수 있다고도 생각할 수 있을 것이다.
무튼 나는 나머지 연산을 보고 dp겠다 싶었고 위의 언급한 부분들을 살펴본 뒤 바로 구현으로 들어갔다.
가지 못하는 부분이 있는데 굳이 boolean 2차원 배열을 또 선언해서 처리하는 것은 비효율적이다. 여기서 거리는 0 이상이어야 하니까 기존 dp 배열에 음수 값으로 못가는 곳을 전처리 해두면 된다.
그리고 위와 왼쪽에서 오는 값을 합산할 때 음수가 될 수도 있다. 이 경우엔 if문이나 삼항연산자, 그리고 Math.max() 등의 방법으로 간단하게 작성 할 수 있을 것이다.
문제 2) 숫자 게임
문제를 처음부터 읽다가 팀이 여러개인줄 알고 약간 겁을 먹었는데 결과적으론 A와 B팀 간의 승부만 가지고 풀면 되는 문제였다.
입출력을 먼저 봤어야 했는데 늘 까먹는 것 같은..
아무튼 이 문제를 요약하면 A팀의 순서(입력으론 무작위로 받은 값)을 알고있을 때 B가 가장 높은 점수를 받는 경우의 승점을 return 하는 문제였다.
여기서 이미 숫자는 부여받은 상태이므로 모든 선수를 어떤 타이밍에 등장시켜도 기존에 가졌던 숫자와 같은 상태로 나오게 된다. 즉, 단순히 A가 가진 숫자들과 B가 가진 숫자들만 잘 비교한 뒤 B가 큰 경우로만 짝을 맺을 수 있는 최대 경우의 수를 구하면 된다.
큰 경우를 어떻게 알 수 있을까
모든 숫자의 대소관계를 계속 비교해서?
그렇게 풀 순 있겠지만 브루트포스이므로 시간복잡도가 꽤나 커질 것으로 예상할 수 있다. 따라서 앞과 뒤의 대소관계를 명확하게 정리할 수 있는 정렬 알고리즘을 통해서 전처리를 한 뒤 투포인터나 이분탐색 등으로 하나씩 비교해 나가면 된다고 생각했다.
그 중 나는 투포인터를 선택했음.
문제 3) 단속카메라
와 오랜만에 문제 하나 푸는데 40분정도 썼다.
이 문제 유형은 할 때마다 헷갈리는데, 이번에 문제를 풀면서 확실하게 정리를 했다. 이젠 제대로 기억해야지.
정리하면서 놀라웠던 점은 다른 알고리즘을 공부할 때 이런 식으로 정리한 부분이 있었는데 로직이 같았다는 점이다. 그리고 그 알고리즘은 세그먼트 트리. 우선 문제 접근부터 하고 차근차근 설명할 예정이다.
우선 문제부터 요약해보면 [-30000, 30000] 구간의 고속도로가 있고 이 도로 위를 달리는 차량들의 모든 구간이 주어졌을 때, 모든 차량을 단속하기 위해서 최소 몇 대의 카메라가 필요한지를 return 해야했던 문제이다.
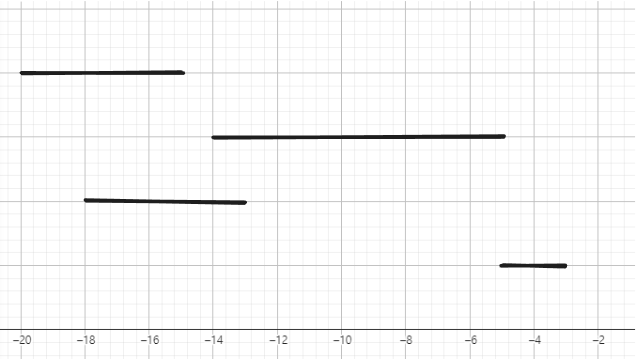
빠른 이해를 위해 입출력 예제인 아래 routes를 손그림으로 풀어보자.
- routes : [[-20,-15], [-14,-5], [-18,-13], [-5,-3]]
- 답 : 2
우선 간단하게 그려보면 아래와 같다.
여기서 눈으로 어떻게 2가 답이 나오는지를 보면 아래와 같다.
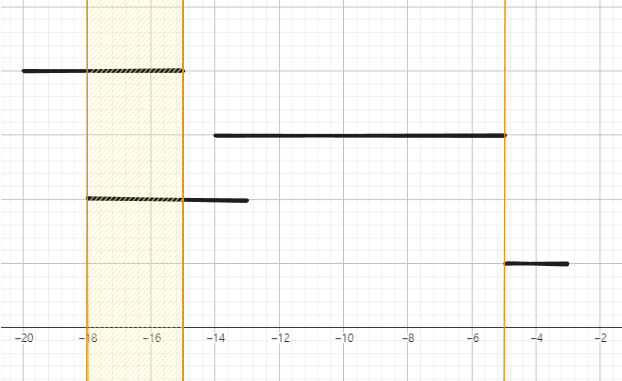
가장 떨어진 [-5,-3] 구간과 [-14,-5] 구간을 주행하는 차량을 같이 단속하기 위해 [-5]에 단속 카메라를 설치해야 한다.
그리고 나머지는 겹치는 부분이 많은데, 온전하게 겹치는 [-18, -15]에 단속 카메라를 설치하면 나머지 두 차량을 단속할 수 있다.
여기까지 보았을 땐 차량의 출발 시작위치와 도착위치가 가장 이를 결정하는 요인이고, 비슷한 값일 수록 같이 단속할 수 있는 확률이 높아진다는 것을 알 수 있다.
그러면 어떨 때 같이 단속할 수 있고 못하는 것인지를 분기를 나눠 확인해 볼 필요가 있다.
경우는 크게 아래 3가지로 나눌 수 있다.
물론 각 경우는 위와 아래를 뒤집었을 때도 있으니 유의하자.
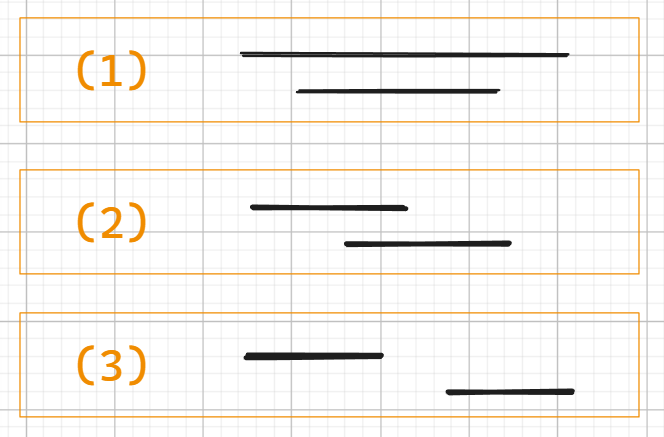
쉬운 이해를 위해 각 경우에 대해서 위의 선분을 prev, 아래의 선분을 cur이라 하고 가장 왼쪽 좌표엔 S, 가장 오른쪽의 좌표엔 E를 넣어 표현하겠음.
우리는 아래의 노란 영역에 카메라를 설치하면 prev와 cur을 둘 다 단속할 수 있음을 잘 알고있다.
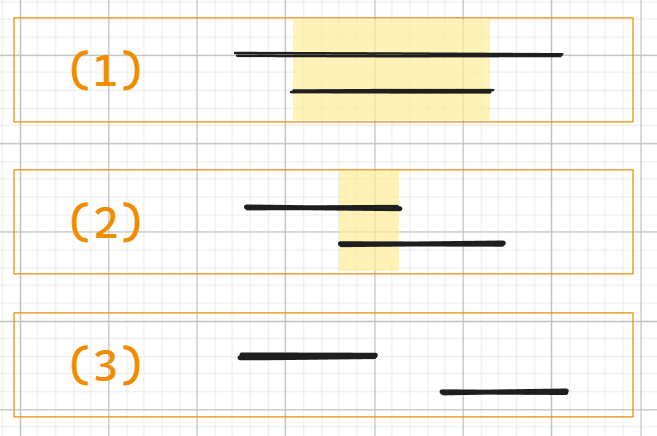
이 노란 영역을 결정하는 권한은 누가 가지고 있는지를 생각하며 하나하나 분석해보자.
그리고 이 권한은 놓을 수 있는 영역인 [putS, putE] 라 하겠음.
- 두 선분 중 하나가 온전히 포함된다.
1) prevS < curS < curE < prevE
2) curS < prevS < prevE < curE
넓은 영역이 온전하게 좁은 영역을 포함한다면 좁은 영역의 선분에게 권한을 주어야한다.
1) prevS < curS < curE < prevE
putS = curS
putE = curE
2) curS < prevS < prevE < curE
putS = prevS
putE = prevE- 일부 겹치는 부분이 있다.
1) prevS < curS < prevE < curE
2) curS < prevS < curE < prevE
두 선분이 온전히 겹치진 않지만, 일부 영역이 겹친다면 겹치는 부분에 권한을 주어야 한다.
1) prevS < curS < prevE < curE
putS = curS
putE = prevE
2) curS < prevS < curE < prevE
putS = prevS
putE = curE- 두 선분에 겹치는 부분이 없다.
1) prevS < prevE < curS < curE
2) curS < curE < prevS < prevE
이 경우엔 무조건 카메라를 하나 더 설치해야함이 보장되므로 카메라 개수를 추가한 뒤 아래 영역에 권한을 위임한다. (다음 순서를 위해)
1) prevS < prevE < curS < curE
putS = curS
putE = curE
2) curS < curE < prevS < prevE
putS = prevS
putE = prevE위 경우를 생각하며 코드를 짜면 좀 더 쉽게 로직을 구현할 수 있을 것이다.
그래서 왜 세그먼트 트리와 로직이 유사하다 했는지를 살펴보면, 세그 트리를 만든 후 값을 찾으러 갈 때도 거의 비슷한 그림을 그려보면 분기를 코드로 쉽게 풀어쓸 수 있기 때문이다.
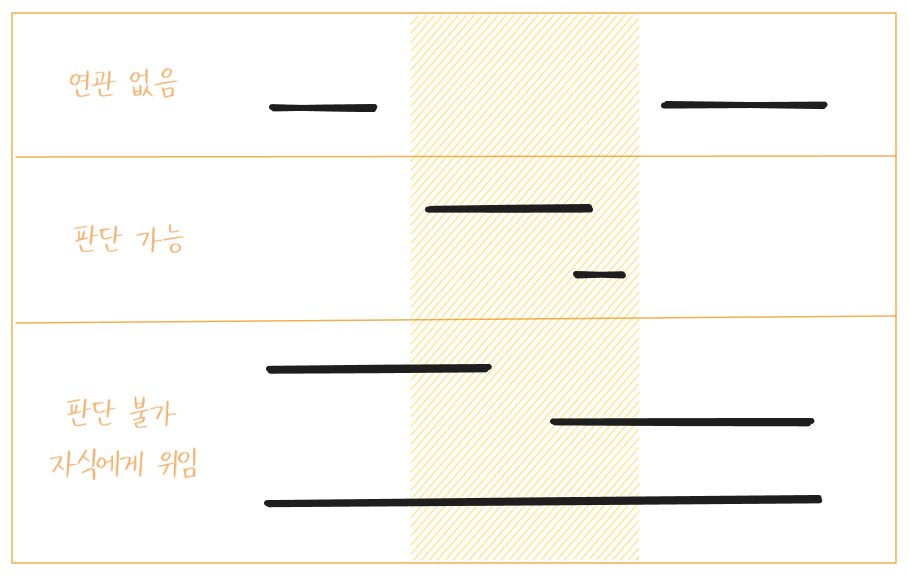
세그먼트 트리를 간단하게 설명하자면, 루트노드는 모든 값을 연산한 값이고 말단 노드는 원본 값 자체를 맡겨둔 노드라 생각하면 된다.
그러면 중간노드들은 말단노드로 부터 연산해서 올라온 값인 것.
그런 연산 값들로 먼저 세그트리를 채운 후에 값을 찾을 때 루트로 부터 내려가는데, 그 때 쓰는 것이 위의 그림이다.
저 형식을 이 문제에 대입시켜볼 줄 생각도 못했는데 여러모로 많은 아이디어를 줬던 문제인 것 같다.
depth 2) 정보처리기사 필기 대비
+) CS 스터디 가이드나 읽어볼까
정처기 공부를 하려했는데 생각보다 집중이 안되서 묵혀둔 CS 스터디 가이드를 펼쳤다. 예전엔 종류별로 스터디를 했었는데 언제부턴가 이상한 사람들이 너무 많아져서 운영이 너무 힘들어졌다. 그래서 근 4개월간 스터디를 안했는데 그 기간동안 덩달아 CS까지 놓아버렸음..
CS 공부는 자의로 하기엔 아직 내가 재미를 못붙였구나 생각해서 강제성을 가져가고자 스터디 가이드를 펼쳤다. 어라 그런데 이거 싸피 들어오기 전에 공부하라 했던 그 내용인걸까 상당히 유사하다.
이걸로 비전공자 친구들은 스터디 진도를 많이 뺐던데 나도 이걸 해볼까 하는 사이 gitlab에 템플릿 있는걸 발견했다.
self-study라.. 상당히 마음에 드는 이름이네.
그래서 내 깃에 그대로 올려두었다. 조금씩 진도를 빼야지!

