짠돌이 호석 문제 풀기

예전부터 PS 목표 1단계가 tony9402님이 선정한 문제 다 풀기였는데.. 역시 마음가짐과 실천은 거리가 있음
https://github.com/tony9402/baekjoon?tab=readme-ov-file#-%EC%A4%91%EC%9A%94%EF%B8%8F%EF%B8%8F-
진짜 언제해😱
그래서 일단 오늘부터 구현만이라도 풀어보기로 함
내일 SSAFY에서 B형 치는데 구현 나오면.. 답없을 것 같아 벼락치기라도 해야겠다 싶었지
그래서 오늘 풀 문제는..!
[21277] 짠돌이 호석 (https://www.acmicpc.net/problem/21277)
이 문제를 선택한 이유는
- Contest에서
류호석님이 낸 문제다 - 질문게시판의 글이 2개뿐이다
- 제출 1087에 맞힌사람이 154명이다
- 정답 비율이 30퍼 미만이다
라는 점이었음
풀다가 지치면 바로 블로그 찾는 나를 막을 수 있을 것 같았고, 류호석님은 보통 신박한 풀이법을 요구하는 문제를 많이 내셨기 때문에 이번 기회로 내 구현력을 레벨업시킬 수 있을 것 같았다!
사실 문제 1시간 보다가 글쓰고 있는건데 진짜 머리가 아프긴하다..
문제분석
제일 중요한건 문제부터 보는 일이지
내 생각의 흐름대로 적어보겠음
입출력
일단 당연하게 입출력 값부터 봤다. 우린 이 값들로 결과를 도출해야하니까 가지고 놀려면 어떤 앤지는 알아야지
첫 줄에 퍼즐의 크기를 나타내는 N1, M1이 공백으로 구분되어 주어진다. 이어서 N1개의 줄에 걸쳐서 완성된 첫 번째 퍼즐의 정보가 주어진다. 각 행마다 M1개의 0 또는 1이 공백없이 주어진다. 다음 줄에 퍼즐의 크기를 나타내는 N2, M2이 공백으로 구분되어 주어진다. 이어서 N2개의 줄에 걸쳐서 완성된 두 번째 퍼즐의 정보가 주어진다. 각 행마다 M2개의 0 또는 1이 공백없이 주어진다. 0이 써있는 격자는 퍼즐 조각이 없는 격자이며 1은 있는 격자이다.
음? 왜 맵이 두개냐
일단 0또는 1이니까 초기 저장값은 boolean 2차원 배열로 저장할 수 있겠네. 근데 이거 저장 어떻게 해두는게 좋을지.. 일단 더 읽어보자
두 퍼즐 모두 4개 모서리에 최소 하나의 1은 존재하는 것이 보장된다.
이 조건은 왜 줬을까.. 보통 이런 문제에 이건 핵심 조건인데 씁
두 개의 퍼즐을 담을 수 있는 액자들 중에 최소 넓이를 출력한다.
두개의 퍼즐을 담는다... 이거 겹쳐야하는구만? (테케보고) 아 이거 어려울 것 같은데;;
1 ≤ N1, M1, N2, M2 ≤ 50
최대가 50인데 4개.. 이거 최적화를 해야할 수 있겠는데
문제읽기
입출력 읽고 대충 뭘 구하라는 건지 느낌은 왔지만 절대 문제를 간과해선 안되니까 다시 읽으러감
두 개의 퍼즐은 각자 N1 행 M1 열과 N2 행 M2 열의 격자 형태로 이루어져 있다.
사실 이 부분 입출력 분석하기 전에 슥 읽었는데 뭔 소린가 싶었음
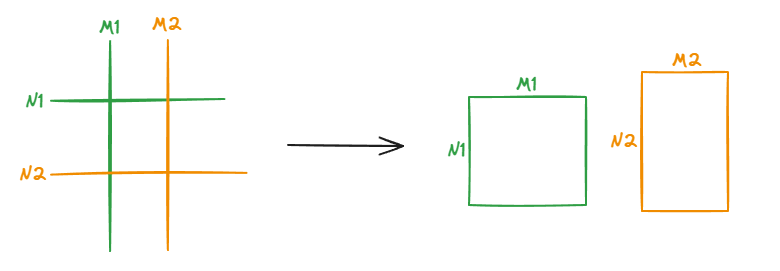
왼쪽이 내가 입출력을 안읽고 이해했을 때고, 우측이 읽고와서 제대로 이해한 거임
역시 입출력은 먼저 봐야해
보관해야 하는 액자를 ~. 액자의 가격은 액자의 넓이(행의 개수 × 열의 개수) 로 결정된다. 즉, 퍼즐 두 개를 퍼즐 조각끼리 같은 격자에서 만나지 않도록 배치해서 하나의 액자에 담는 방법 중에 가장 적은 비용일 때를 찾아보자! 단, 각 퍼즐은 90도, 180도, 270도로 자유롭게 회전시켜도 된다.
ㅎㅎ 우려했던 생각이 맞긴했네.
이거 두개의 맵을 각각 회전하는 조합도 찾아야하고.. 그 두 맵을 상하좌우에서 맞추는 경우도 생각해야하는데
아.. 이거 크기가 안맞을 수 있으니까 한칸이라도 겹칠동안 슬라이드 하면서 또 찾아야하네!?
음.. 이때부터 망함을 좀 직감하긴 했음
풀 수 있을까 싶었는데 하긴해야지 뭐
시간복잡도 계산
하 아직도 이 식이 정확한지도 모르겠음
- 일단 두 퍼즐은 시계방향으로 4번 회전 가능
- 만들어진 퍼즐은 하나는 가만히 있고 하나는 붙인다고 생각하면 4개의 경우가 있음
- 퍼즐 두개의 각 한면씩 접한 뒤 한칸씩 들어가야하는데, 그 전에 두 퍼즐이 한칸 이상 접할 모든 경우를 봐야함
- 그 경우 속에서 이게 겹쳐질 수 있으니까 들어갈 수 있을 때 (들어가는 방향과 평행한 축의 길이 중 최댓값)까지 들어가야 함
for(1번 : 두 퍼즐을 회전할 경우의 수; 4+3+2+1 = 10)
둘 다 회전하고 나서 (50*50*50*50)
for(2번 : 붙일 곳을 정한다; 4)
for(3번 : 겹치기 위해 나아가는 방향의 수직과 평행한 길이; 2*50-1)
for(4번 : 겹치기 / 겹치기 위해 나아가는 방향과 평행한 길이 중 최댓값; 50)
=> 10 * (50*50*50*50) * 4 * (2*50-1) * 50 = 1,237,500,000,000 (불가능)어우 저게 될 수가 없지
그런데 회전하는 경우를 뺀다면..?
10 * 4 * (2*50-1) * 50 = 198,000 (*가능)이거... 구현 진짜 장난 아니겠다 ㅎㅎㅎㅎ
아아 벌써부터 베스트프렉티스 보고 싶어 ㅠㅠㅠㅠㅠ
코드 구현
하 일단 구현력 기르는데 직방일 것 같으니 도움은 될텐데...
어라 근데 오늘 채용설명회가 있네~~ 미뤄야지 ㅎㅎㅎㅎㅎ
