그래프 이론 기초

boostcourse에서 제공하는 그래프와 추천시스템 그래프 이론 기초에 대한 강의 내용을 정리했다.

00. 학습 내용

• 그래프의 정의에 대하여 학습
• 그래프 관련 AI 문제에 대하여 학습
• 그래프 기초 개념에 대하여 학습

01. 그래프의 정의

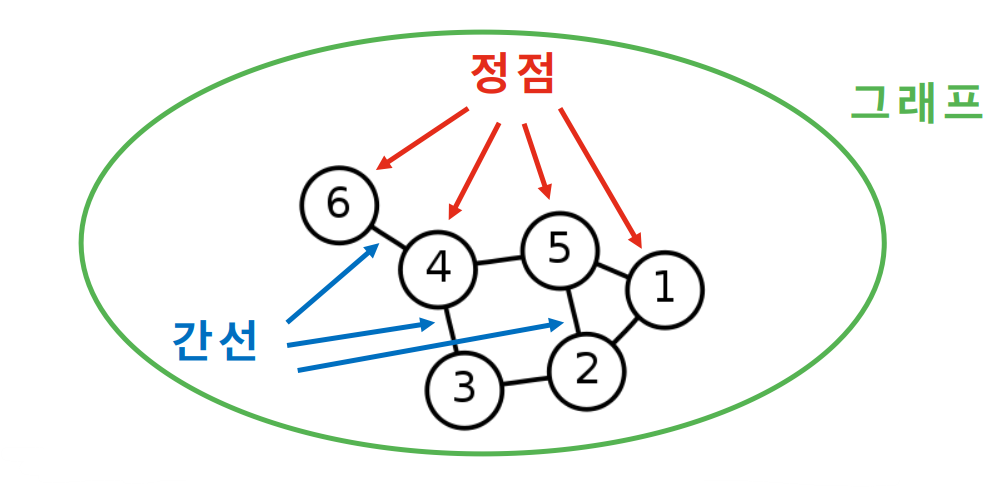
• 그래프(Graph)는 정점 집합과 간선 집합으로 이루어진 수학적 구조
• Graph == Network / Vertex(정점) == Node / 간선 == Edge == Link
• 보통 정점들의 집합을 V, 간선들의 집합을 E, 그래프를 G = (V, E)로 표현

• 우리 주변에는 많은 복잡계(Complex System)가 존재(구성 요소 간의 복잡한 상호작용을 특징으로 함)
• 그래프는 복잡계를 효과적으로 표현하고 분석하기 위한 언어
• 복잡계는 구성 요소들 간의 상호작용으로 이루어지고, 상호작용을 표현하기 위한 수단으로 그래프가 널리 사용됨
• 복잡계를 이해하고, 복잡계에 대한 정확한 예측을 하기 위해서는 복잡계 이면에 있는 그래프에 대한 이해가 반드시 필요
• 그래프를 공부함으로써 복잡계가 등장하는 수많은 분야에 활용할 수 있고, 전산학, 물리학, 생물학, 화학, 사회과학 등이 그 예시

02. 그래프 관련 AI 문제

• 정점 분류(Node Classification) 문제
  • 트위터에서의 공유(Retweet) 관계를 분석하여, 각 사용자의 정치적 성향 파악
  • 단백질의 상호작용을 분석하여, 단백질의 역할 파악
• 연결 예측(Link Prediction) 문제
  • 페이스북 소셜네트워크의 진화 파악
• 추천(Recommendation) 문제
  • 
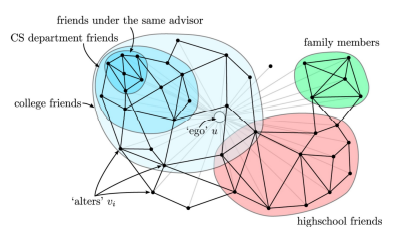
• 군집 분석(Community Detection) 문제
  • 연결 관계로부터 사회적 무리(Social Circle) 파악
  • 
• 랭킹(Ranking) 및 정보 검색(Information Retrieval) 문제
  • 웹(Web)이라는 거대한 그래프로부터 어떻게 중요한 웹페이지를 찾을 수 있는가?
• 정보 전파(Information Cascading) 및 바이럴 마케팅(Viral Marketing) 문제
  • 정보는 네트워크를 통해 어떻게 전달될까? 어떻게 정보 전달을 최대화 할 수 있을까?

03. 그래프 기초 개념

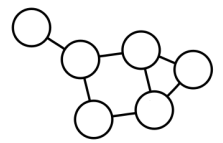
• 간선에 방향이 없는 그래프(Undirected Graph)
  • 협업 관계 그래프
  • 페이스북 친구 그래프

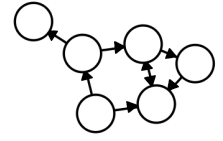
• 간선에 방향이 있는 그래프(Directed Graph)
  • 인용 그래프
  • 트위터 팔로우 그래프

• 간선에 가중치가 없는 그래프(Unweighted Graph)
  • 웹 그래프
  • 페이스북 친구 그래프

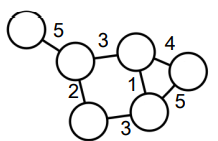
• 간선에 가중치가 있는 그래프(Weighted Graph)
  • 전화 그래프
  • 유사도 그래프

• 동종 그래프(Unpartite Graph)
  • 동종 그래프는 단일 종류의 정점을 가짐
  • 웹 그래프
  • 페이스북 친구 그래프

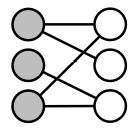
• 이종 그래프(Bipartite Graph)
  • 이종 그래프는 두 종류의 정점을 가짐
  • 다른 종류의 정점사이에만 간선이 연결됨
  • 전자 상거래 구매내역 (사용자, 상품)
  • 영화 출연 그래프 (배우, 영화)

• 위 전자상거래 구매내역은 방향이 없는, 가중치가 있는, 이종 그래프라고 할 수 있음

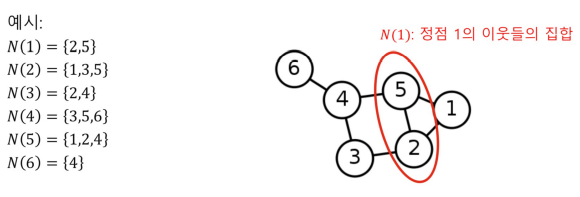
• 정점의 이웃(Neighbor)은 그 정점과 연결된 디른 정점을 의미
  • 정점 v의 이웃들의 집한을 보통 N(v) 혹은 $N_{v}$ 로 표현

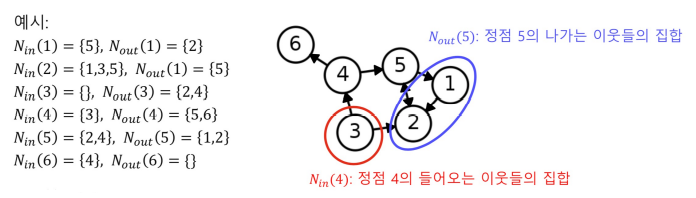
• 방향성이 있는 그래프에서는 나가는 이웃과 들어오는 이웃으로 구분
  • 나가는 이웃의 집합을 $N_{out}(v)$로 표현
  • 들어오는 이웃의 집합을 $N_{in}(v)$로 표현