페이지 랭크

boostcourse에서 제공하는 그래프와 추천시스템 페이지 랭크에 대한 강의 내용을 정리했다.

00. 학습 내용

• 페이지 랭크의 정의에 대하여 학습
• 페이지 랭크의 계산 방법에 대하여 학습

01. 페이지 랭크의 정의

• 페이지 랭크란 사용자 키워드와 관련성이 높고 신뢰할 수 있는 웹페이지를 찾는 방법이라고 할 수 있음
• 페이지 랭크는 크게 투표 관점과 Random Walk 관점으로 나뉨

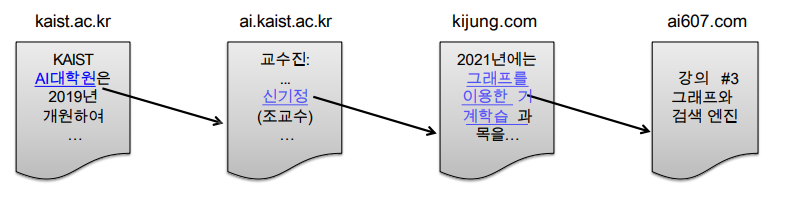
• 투표 관점의 페이지랭크
  • 투표를 통해 사용자 키워드와 관련성이 높고 신뢰할 수 있는 웹페이지를 찾음
  • 투표의 주체는 웹페이지, 하이퍼링크를 통해 투표
  • 들어오는 간선이 많을 수록, 즉 많은 하이퍼링크가 있을 수록 신뢰할 수 있는 웹페이지 (단순히 간선의 수를 세는 것은 악용의 소지가 있기 때문에 가중 투표 방식을 활용)
  • 재귀(Recursion), 즉 연립방정식 풀이를 통해 페이지랭크 점수(측정하려는 웹페이지의 관련성 및 신뢰도)를 계산
  • 
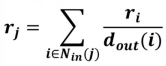
• Random Walk 관점의 페이지랭크
  • 임의 보행을 통해 웹을 서핑하는 웹서퍼를 가정
  • 웹서퍼는 현재 웹페이지에 있는 하이퍼링크 중 하나를 균일한 확률로 클릭하는 방식으로 웹을 서핑
  • 웹서퍼가 t번째 방문한 웹페이지가 웹페이지 t일 확률을 $p_{i}(t)$이며, $p(t)$는 길이가 웹페이지 수와 같은 확률분포 벡터
  • 
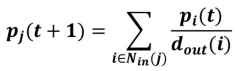
  • 웹서퍼가 이 과정을 무한히 반복하고 나면, 즉 t가 무한히 커지면,
    확률 분포는 $p(t)$는 수렴 (마르코프 체인, 확률은 수렴한다)
  • 즉, $p(t)$ = $p(t + 1)$ = $p$ 가 성립
  • 수렴한 확률 분포 $p$는 정상 분포(Stationary Distribution)라 부름
  • 

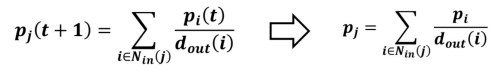
• 결국, 투표 관점에서 정의한 페이지 랭크 점수와 임의 보행 관점에서의 정상 분포는 서로 동일

02. 페이지 랭크의 계산 방법

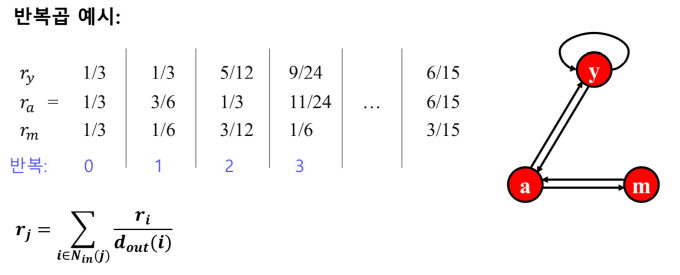
• 페이지랭크 점수의 계산은 반복곱(Power Iteration)을 사용
  (1) 각 웹페이지 i의 페이지랭크 점수 $r^{(0)}_{i}$를 동일하게 1 / 웹페이지의 수 로 초기화
  (2) 페이지랭크 식을 이용하여 페이지랭크 점수릉 갱시
  (3) 페이지 랭크 점수가 수렴하면 종료

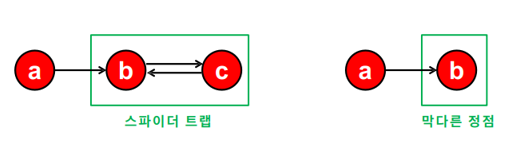
• 들어오는 간선은 있지민 나가는 간선은 없는 정점 집합인 Spider Trap 문제
• 들어오는 간선은 있지만 나가는 간선은 없는 Dead End 문제
• 위 문제들에 의해 반복곱은 항상 수렴을, 합리적인 점수를 보장하지 않음

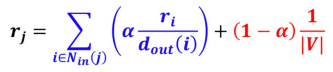
• 반복곱의 문제를 해결하기 위해서 Teleport를 도입
• 임의 보행 관점에서, 웹을 서핑하는 웹서퍼의 행동을 다음과 같이 수정
  (1) 현재 웹페이지에 하이퍼링크가 없다면, 임의의 웹페이지로 순간이동
  (2) 현재 웹페이지에 하이퍼링크가 있다면, 앞면이 나올 확률이 $a$인 동전을 던짐
  (3) 앞면이라면, 하이퍼링크 중 하나를 균일한 확률로 선택해 클릭
  (4) 뒷면이라면, 임의의 웹페이지로 순간이
• $a$를 감폭 비율(Damping Factor)이라고 부르며 값으로 보통 0.8 정도를 사용
• 각 막다른 정점에서 (자신을 포함) 모든 다른 정점으로 가는 간선을 추가한 방식
• 위 수식을 이용하여 반복곱을 수행
  • $|V|$는 전체 웹페이지의 수
  • 파란색 부분은 하이퍼링크를 따라 정점 j에 도착할 확률을 의미
  • 빨간색 부분은 순간이동을 통해 정점 j에 도착할 확률을 의미

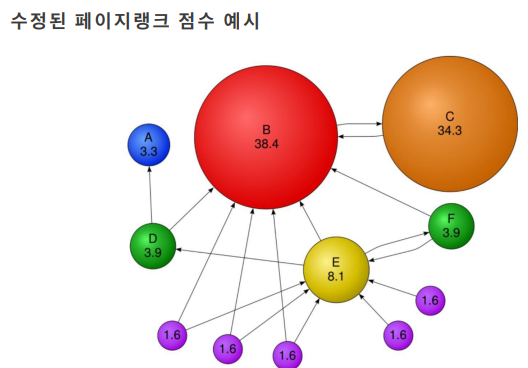
• 가중합을 이용하기 때문에, 신뢰할 수 있는 웹페이지의 1표를 매우 중요하게 여긴다는 것을 알 수 있다.
• 여기서 신뢰한다는 것은, 많은 하이퍼링크로 연결되며 많은 하이퍼링크가 연결된 웹페이지의 하이퍼링크가 연결되어 있다는 것이다.