[TIL: 0222] 이진트리

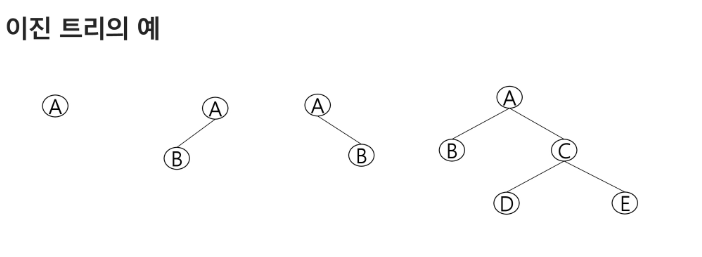
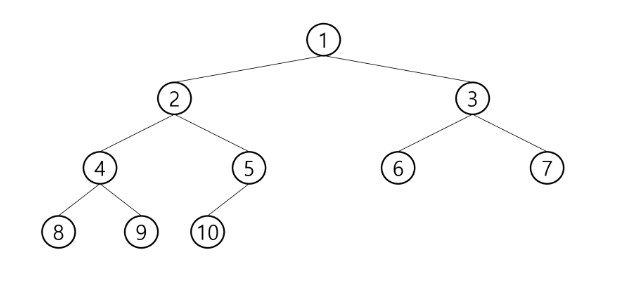
트리

비선형 구조
원소들 간에 1:n 관계
계층형 자료구조
상위원소에서 하위원소로 내려가면서 확장되는 트리 모양의 구조

• 한 개 이상의 노드로 이루어진 유한 집합
  노드 중 최상위 노드는 루트(root)
  나머지 노드들은 n(>= 0)개의 분리 집합으로 분리될 수 있다

T1... TN은 하나의 트리가 되며(재귀적 정의) 루트의 부 트리 라고 한다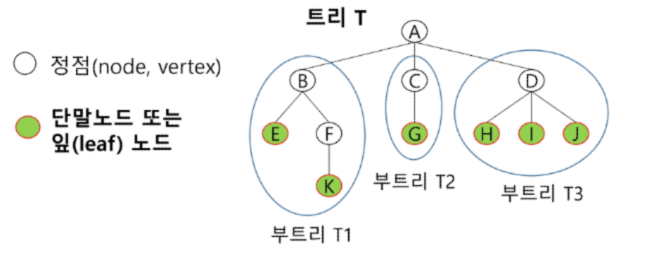

• 노드(node): 트리의 원소
• 간선(edge): 노드를 연결하는 선, 부모 노드와 자식 노드를 연결
• 루트 노드(root node): 트리의 시작 노드
  위 트리 A 의 루트노드는 A
• 형제 노드: 같은 부모 노드의 자식 노드들
  B, C, D
• 조상 노드: 간선 따라 루트 노드까지 이르는 경로에 있는 모든 노드들
  K의 조상 노드는 F, B, A
• 서브 트리: 부모 노드와 연결된 간선을 끊었을 때 생성되는 트리
• 자손 노드: 서브 트리에 있는 하위 레벨의 노드들
  B의 자손 노드는 E, F, L

차수(degree)

• 노드의 차수: 노드에 연결된 자식 노드의 수
  B의 차수 = 2, C의 차수 = 1
• 트리의 차수: 트리의 노드의 차수 중에서 가장 큰 값
  트리 T의 차수 = 3
• 단말 노드(리프 노드): 차수가 0인 노드, 자식이 없는 노드

높이

• 노드의 높이: 루트에서 노드에 이르는 간선의 수, 노드의 레벨 (절대적인건 아니다 0기준, 1기준에 따라 다르다)
  B의 높이 = 1, F의 높이 = 2
• 트리의 높이: 트리 노드 높이 중에서 가장 큰 값
  트리 T의 높이 = 3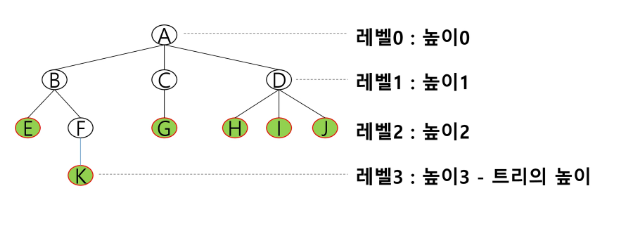

이진 트리

모든 노드들이 2개의 서브트리를 갖는 특별한 형태의 트리

• 각 노드가 자식 노드를 최대한 2개까지만 가질 수 있는 트리
  왼쪽 자식 노드
  오른쪽 자식 노드

*자식은 또 누군가의 부모가 될 수 있다

레벨 i에서 노드의 최대 개수는 2의 i제곱 개
높이가 h인 이진 트리가 가질 수 있는 노드의 최소 개수는 (2의 h제곱)개 (자식이 한개씩만 있다면)가 되며, 최대 개수는 (2의 h + 1 제곱 + 1)개가 된다

포화 이진 트리(중요)

모든 레벨에 노드가 포화 상태로 차 있는 이진 트리

• 높이가 h일 때, 최대 노드 개수인 (2의 h + 1 제곱 + 1)개의 노드를 가진 이진 트리
  높이 3일 때 222*2 - 1 = 15개의 노드ㅠ

• 루트를 1번으로 하여 정해진 위치에 대한 노트 번호를 가진

완전 이진 트리

높이가 h이고 노드 수가 n개일 때 포화 이진 트리의 노드 번호 1번부터 n번까지 빈 자리가 없는 이진 트리
*포화이진트리 특성도 알고 있어야 함

편향 이진 트리

높이 h에 대한 최소 개수의 노드를 가지면서 한 쪽 방향의 자식 노드만을 가진 이진 트리

• 왼쪽 편향 / 오른쪽 편향

이진트리 - 순회(traversal)

순회: 트리 노드들을 체계적으로 방문하는 것

• 3가지 기본 순회방법 (가장 중요)
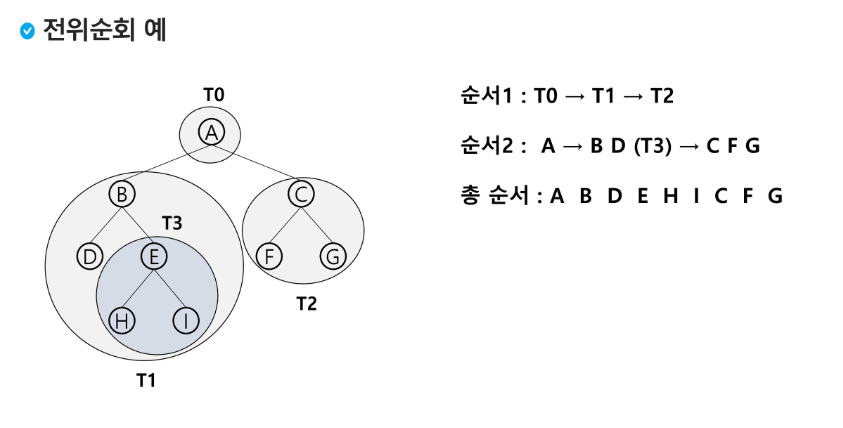
  전위순회: VLR
  부모노드 > 자식노드 좌 > 자식노드 우
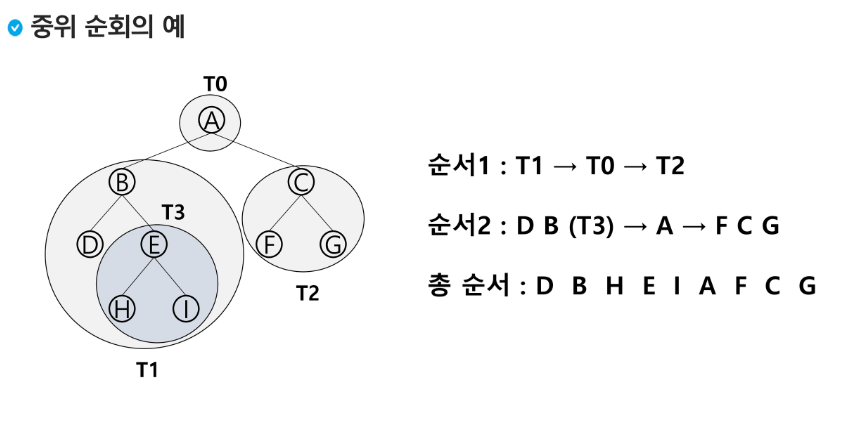
  중위순회: LVR
  자식노드 좌 > 부모노드 > 자식노드 우
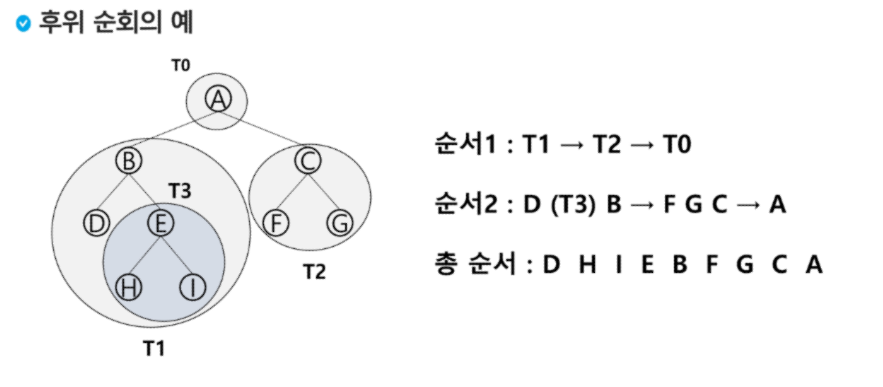
  후위순회: LRV
  자식노드 좌 > 자식노드 우 > 부모노드

전위 순회

1. 현재 노드 n을 방문해 처리 > V
2. 왼쪽 서브트리로 이동 > L
3. 오른쪽 서브트리로 이동 > R갔다가 아무것도 없으면 돌아가서 빠져나온다

중위 순회

1. 현재 노드 n을 왼쪽 서브트리로 이동 > L
2. 현재 노드 n을 방문 처리 > V
3. 현재 노드 n의 오른쪽 서브트리로 이동 > R
   왼쪽에서 온 것만 처리

후위 순회

1. 현재 노드 n의 왼쪽 서브트리로 이동 > L
2. 현재 노드 n의 오른쪽 서브트리로 이동 > R
3. 현재 노드 n을 방문 처리 > V오른쪽에서 온 것만 처리

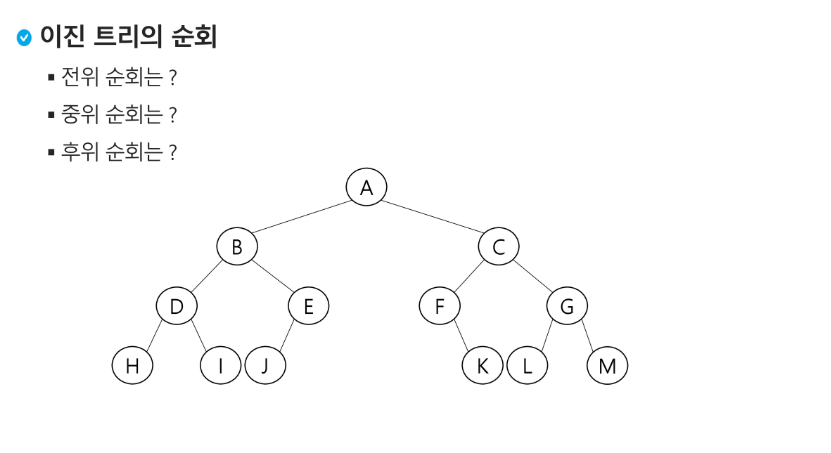
• 전위순회
  A B D H I E J C F K G L K
• 중위순회
  H D I B J E A F K C L G M
• 후위순회
  H I D J E B K F L M G C A

이진트리의 표현

배열을 이용한 이진트리의 표현

이진 트리에 각 노드 번호를 다음과 같이 부여
루트 번호를 1로 함
레벨 n에 있는 노드에 대하여 왼쪽부터 오른쪽으로 2의n제곱부터 2의 n+1제곱 -1 까지 번호를 차례대로 부여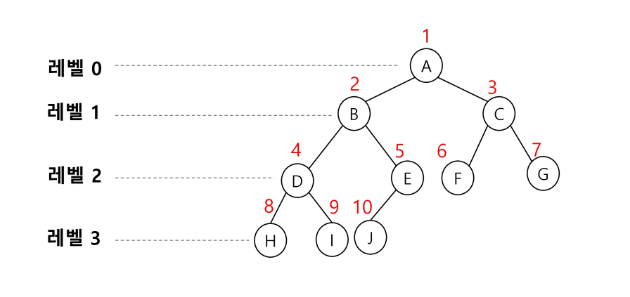

노드 번호의 성질

• 노드번호가 i인 부모노드번호 i//2
• 왼쪽 자식번호는 2 * i
• 오른쪽 자식 번호 2 * i + 1
• 레벨 n의 노드 시작 번호 2의n제곱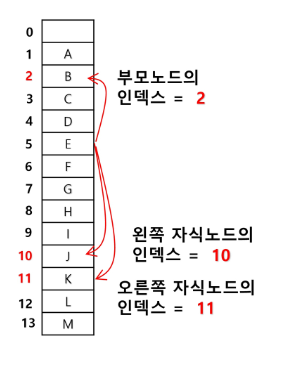7번의 부모는 7//2 = 3

배열을 이용한 이진 트리 표현

노드 번호를 배열 인덱스로 사용
높이가 h인 이진 트리를 위한 배열 크기

이진 트리의 저장

• 부모 번호를 인덱스로 자식 번호를 저장
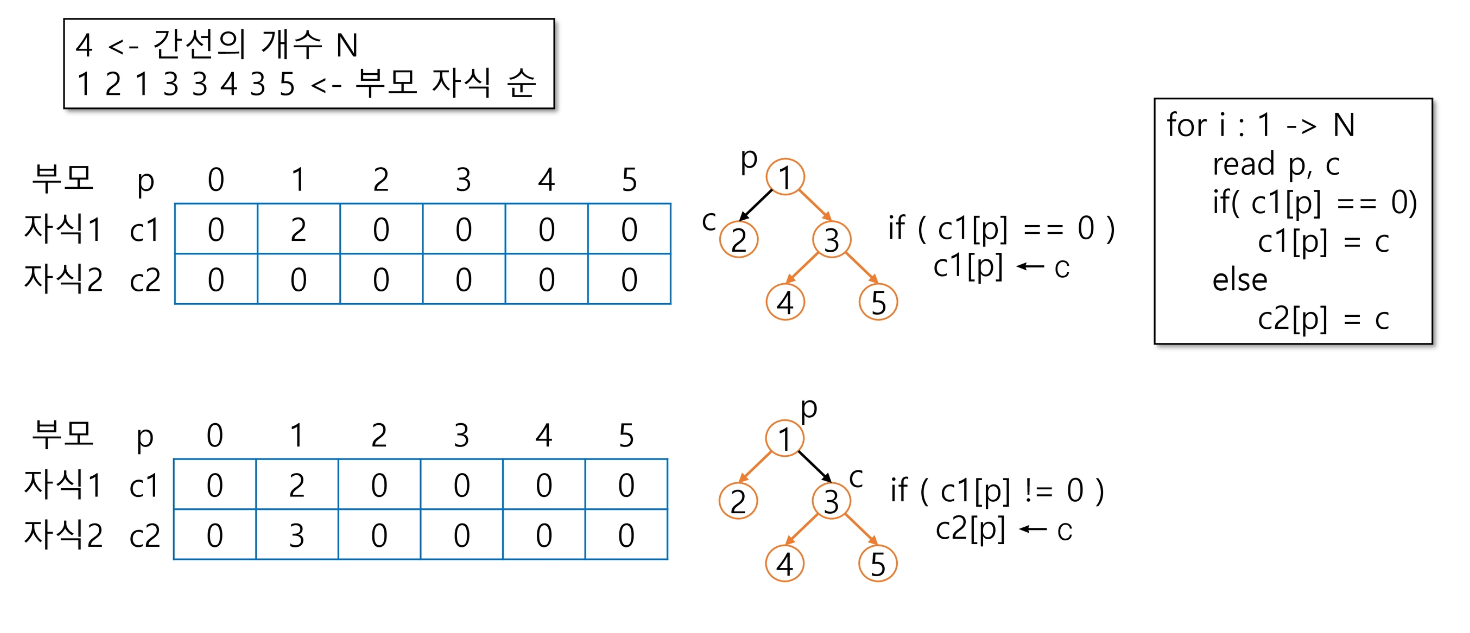
  *노드는 간선의 개수보다 1개 더 많다
  부모 번호를 인덱스로 자식 번호를 저장한다
  최대 자식이 두개니까 열이 두 개
  특별한 자식간 규칙이 없으면 저장한 순서대로 자식을 생각
  (왼쪽 자식 번호가 더 작아야된다는 규칙 등)

• 자식 번호를 인덱스로 부모 번호를 저장
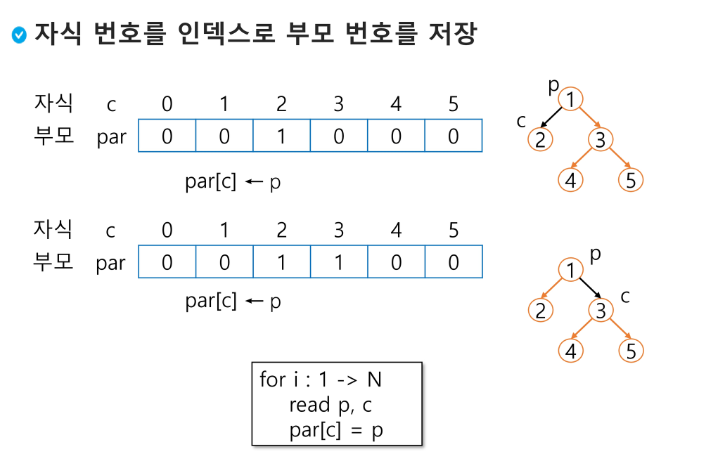
  *부모는 하나밖에 없기 때문에 일차원 배열 하나
  부모를 찾고 싶다면 리스트를 보면서 부모가 없는 애(0이거나 -1)를 찾으면 루트다
  조상을 찾고 싶다면 찾는 노드부터 없는 부모가 없는 곳 까지 찾아가면 조상 노드들이다

• 루트 찾기, 조상 찾기

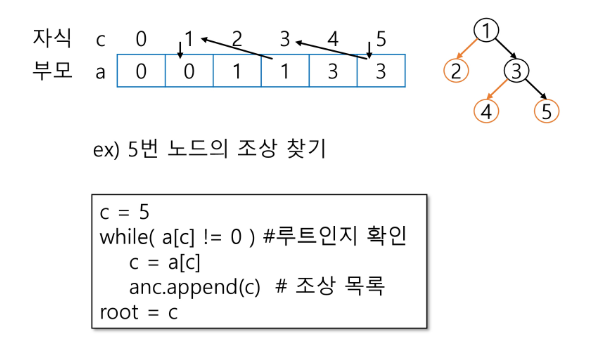
c = 5
while(a[c] != 0) # 루트인지 확인
	c = a[c]
    anc.append(c) # 조상 목록
root = c