Dijkstra Algorithm
다익스트라 알고리즘 (데이크스트라 알고리즘)
- 도로 교통망 같은 곳에서 나타날 수 있는 그래프에서 꼭짓점 간의 최단 경로를 찾는 알고리즘의 한 종류
- 단일 출발지에서 최단 경로를 찾는 알고리즘
- 음의 가중치가 없는 경우에 적용 가능
단일 출발지에서 최단 경로를 찾는 알고리즘
- 특정한 하나의 정점에서 그래프의 다른 모든 정점으로 가는 최단경로를 알려찾는 알고리즘
- 그래프에서 주어진 정점에 대해서 그 노드와 다른 모든 꼭짓점 간의 가장 짧은 경로를 탐색
영상 : 파이썬 클래스
음의 가중치가 없는 경우에 적용 가능
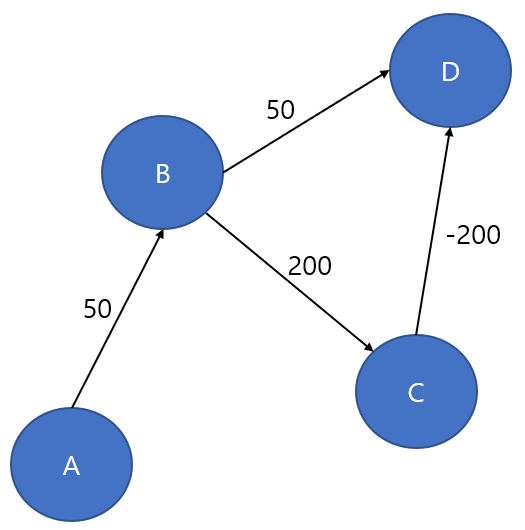
위와 같이 경로에 음수가 있는 경우는 다익스트라 알고리즘 적용 불가능
만약 음의 가중치가 있는 경우는 벨만-포드 알고리즘을 사용해야 함
시간 복잡도
정점 개수가 V, 간선 개수가 E일 때 기본적인 최적화를 거치면 O(ElogV)
다익스트라 알고리즘 작동 과정
- 아직 방문하지 않은 정점들 중 거리가 가장 짧은 정점을 하나 선택해 방문
- 해당 정점에서 인접하고 아직 방문하지 않은 정점들의 거리를 갱신
예시
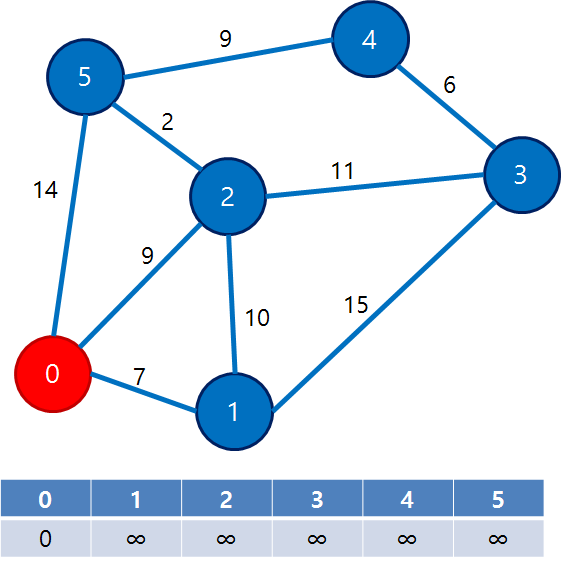
- 아직 확인되지 않은 거리는 초기값을 무한으로 두고 시작
- 정점 i, j 사이의 거리를 d, 거리 테이블을 dist인 경우
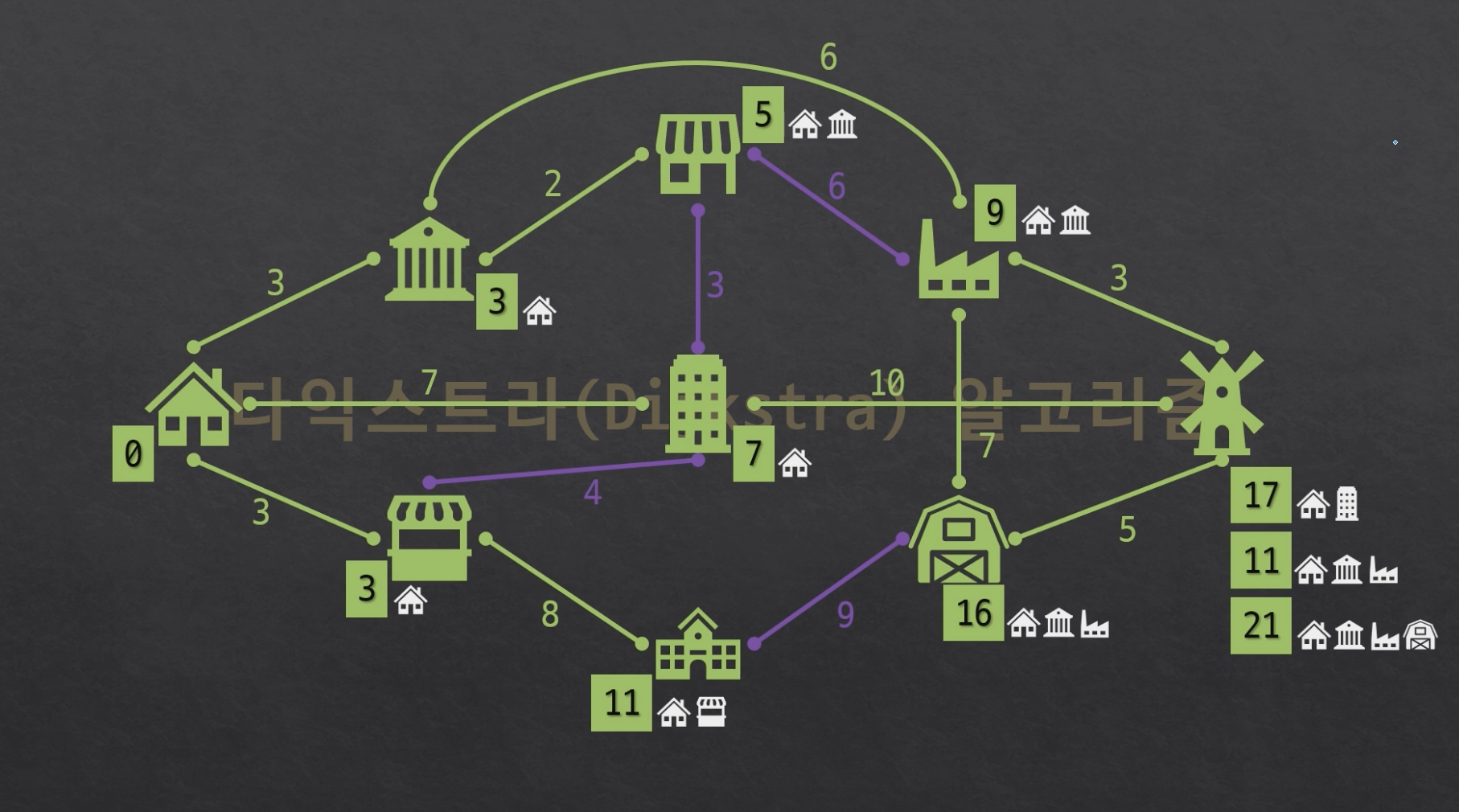
0번 정점을 시작점으로 하여 0번에서 다른 정점으로 가는 최단 경로를 구하기
dist가 제일 작은 것이 시작점 (나머지는 다 무한)
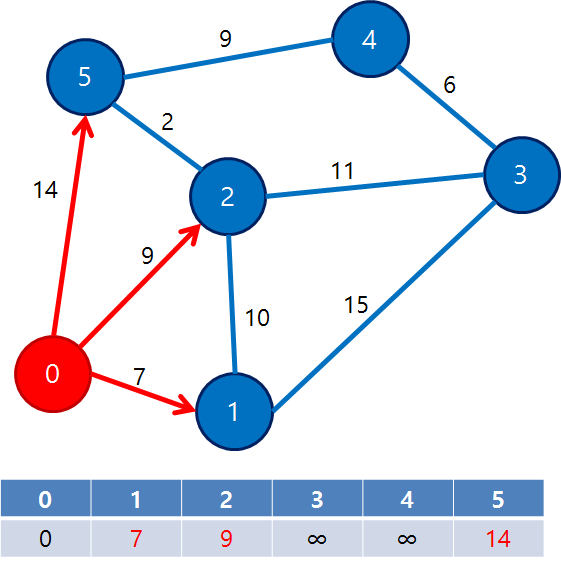
시작점인 0번에서 바로 갈 수 있는 인접한 정점은 1, 2, 5번 정점이고, 0번을 통해 k번 정점으로 가는 거리는 dist[0] + d[0][k]이고
만약 0번을 통해 k번 정점으로 가는 거리가 dist[k]보다 작다면 dist[k]가 갱신됨
지금은 0번을 제외한 모든 정점으로의 dist 값이 무한대이므로 무조건 갱신됨
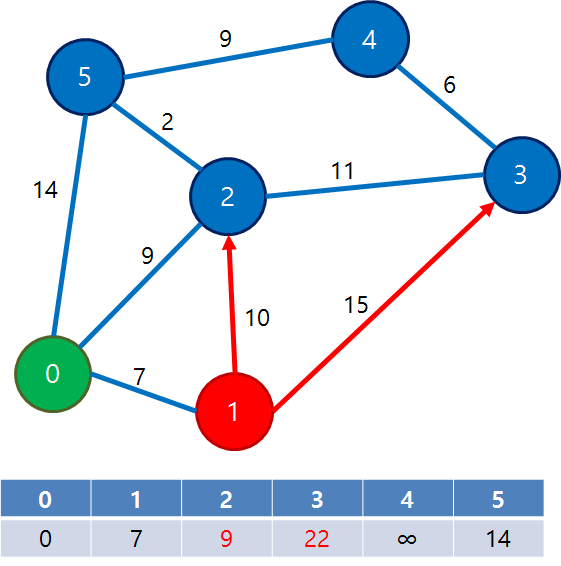
그 다음 아직 방문하지 않은 정점 중 dist가 제일 작은 곳이 1번이므로 1번 정점을 방문
1번 정점 방문 후 인접한 2, 3번 정점의 거리 갱신을 시도
0번 정점 또한 인접하지만 0번 정점은 이미 방문한 상태이므로 아무것도 하지 않음
여기서 2번 정점의 경우는 거리가 갱신되지 않음 --> dist[2]가 이미 dist[1] + d[1][2]보다 작거나 같기 때문
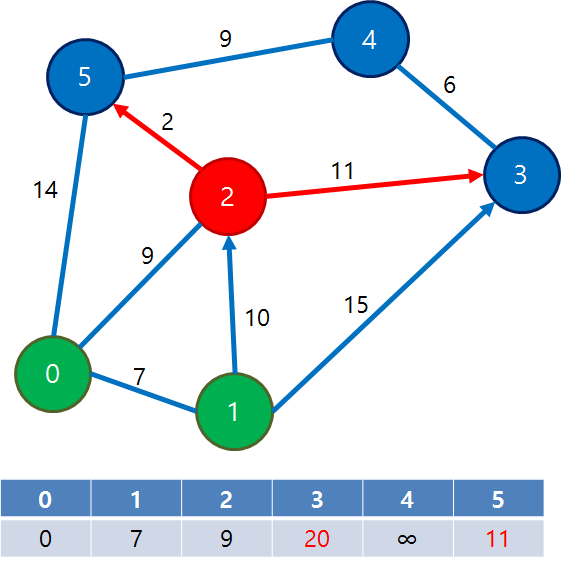
이번에는 dist[2]가 제일 작으므로 2번 정점을 방문하여 3, 5번 정점으로의 거리를 갱신함
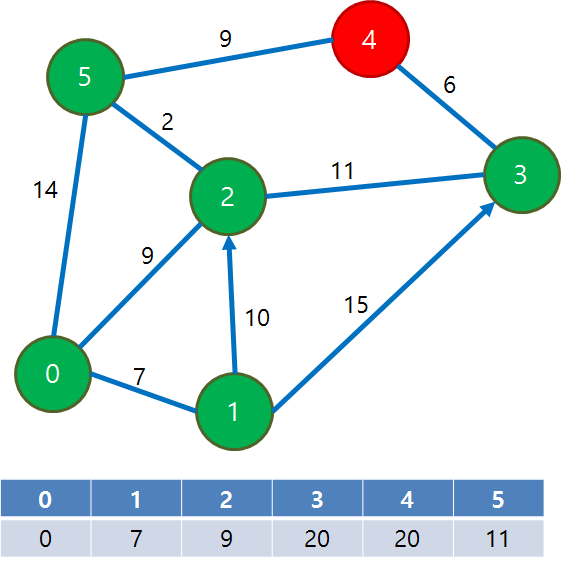
이 과정을 반복하여 마지막으로 4번 정점만 남았을 때는 나머지 정점을 다 방문한 상태이므로 아무것도 하지않음
과정이 끝나고 나면 각 dist 값이 0번 정점으로부터의 실제 최단 거리가 됨
사용 예시
네트워크 라우팅 프로토콜에서 널리 이용됨
아래의 예시에서 주로 사용됨
- IS-IS (Intermediate System to Intermediate System)
- OSPF(Open Shortest Path First: 최단 경로 우선 프로토콜)
ref
위키백과 - 데이크스트라 알고리즘
파이썬 클래스
음수 가중치 : 프로그래밍 학습 블로그
중코대 블로그
waca's field
문제 예시 : 라이 블로그