Greedy Algorithm (탐욕 알고리즘)
-
최적해를 구하는 데에 사용되는 근사적인 방법
-
동적 계획법의 단점을 극복하기 위하여 만들어진 알고리즘
-
여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달
-
순간마다 하는 선택은 그 순간에 대해 지역적으로는 최적
-
최종적인 해답(전역적인 해답)이 최적이라는 보장은 없음
탐욕 알고리즘 예시
최대값을 구하는 경우
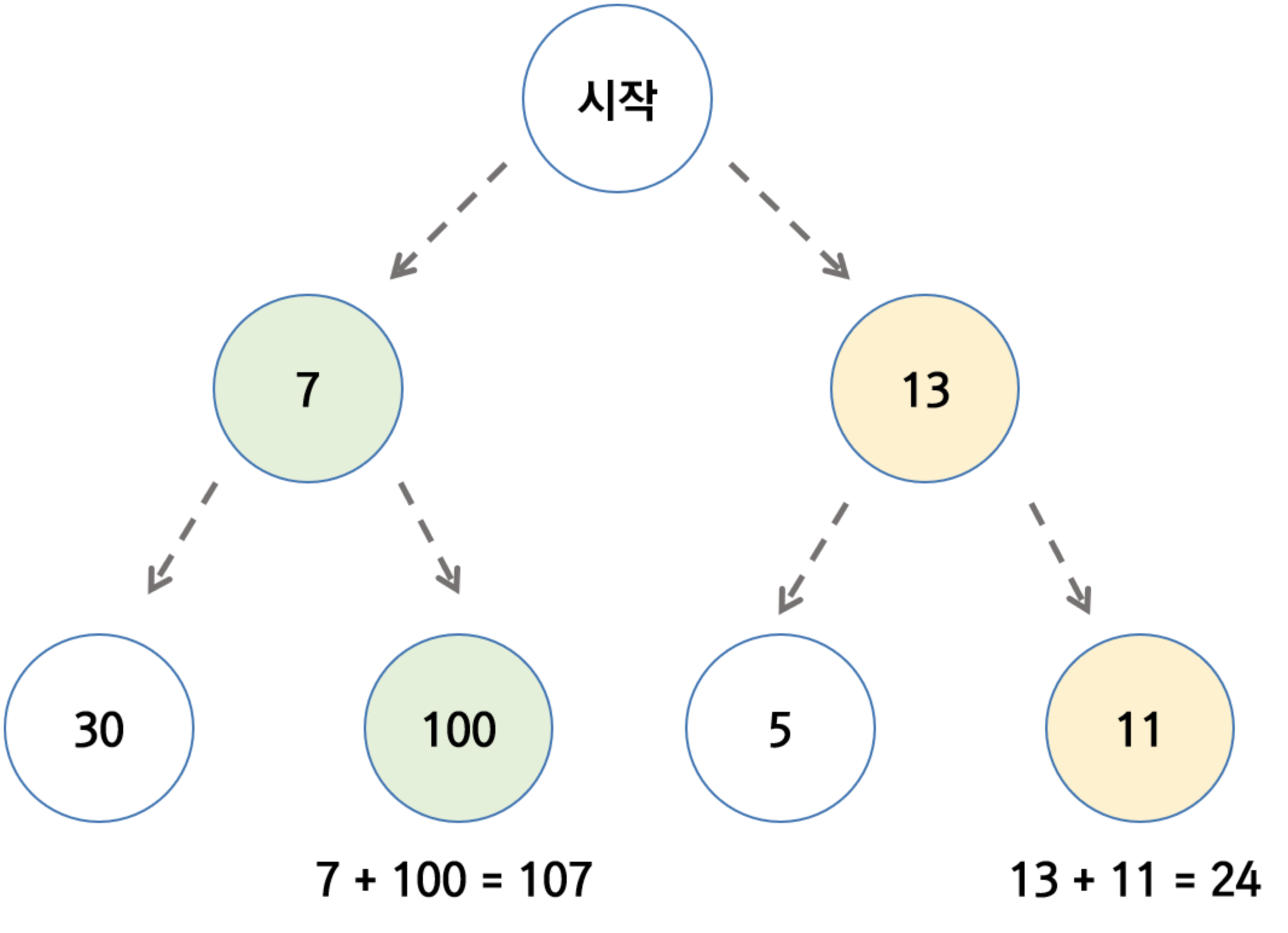
탐욕 알고리즘을 사용했을 경우
- 첫번째 선택 : 7과 13 중에서 더 큰 값인 13을 선택
- 탐욕 알고리즘의 최종적인 해 --> 24
위의 예시와 같이 탐욕 알고리즘을 사용한 경우의 최종적인 해는 24이다. 그러나 실제의 최대값은 107이다.
탐욕 알고리즘은 순간마다 최적으로 생각되어지는 값을 선택하게 된다. 따라서 최종적인 해답이 최적값이라는 보장이 없다.
적용 가능한 경우
지역적으로 최적이면서 전역적으로 최적인 문제
조건
탐욕 알고리즘 적용이 가능한 문제들은 대부분 아래의 두 조건을 만족
탐욕스런 선택 조건(Greedy choice property)
- 앞의 선택이 이후의 선택에 영향을 주지 않음
최적 부분 구조 조건(Optimal substructure)
- 문제에 대한 최적해가 부분 문제에 대해서도 역시 최적해
적용 가능 예시
1. 활동 선택 문제
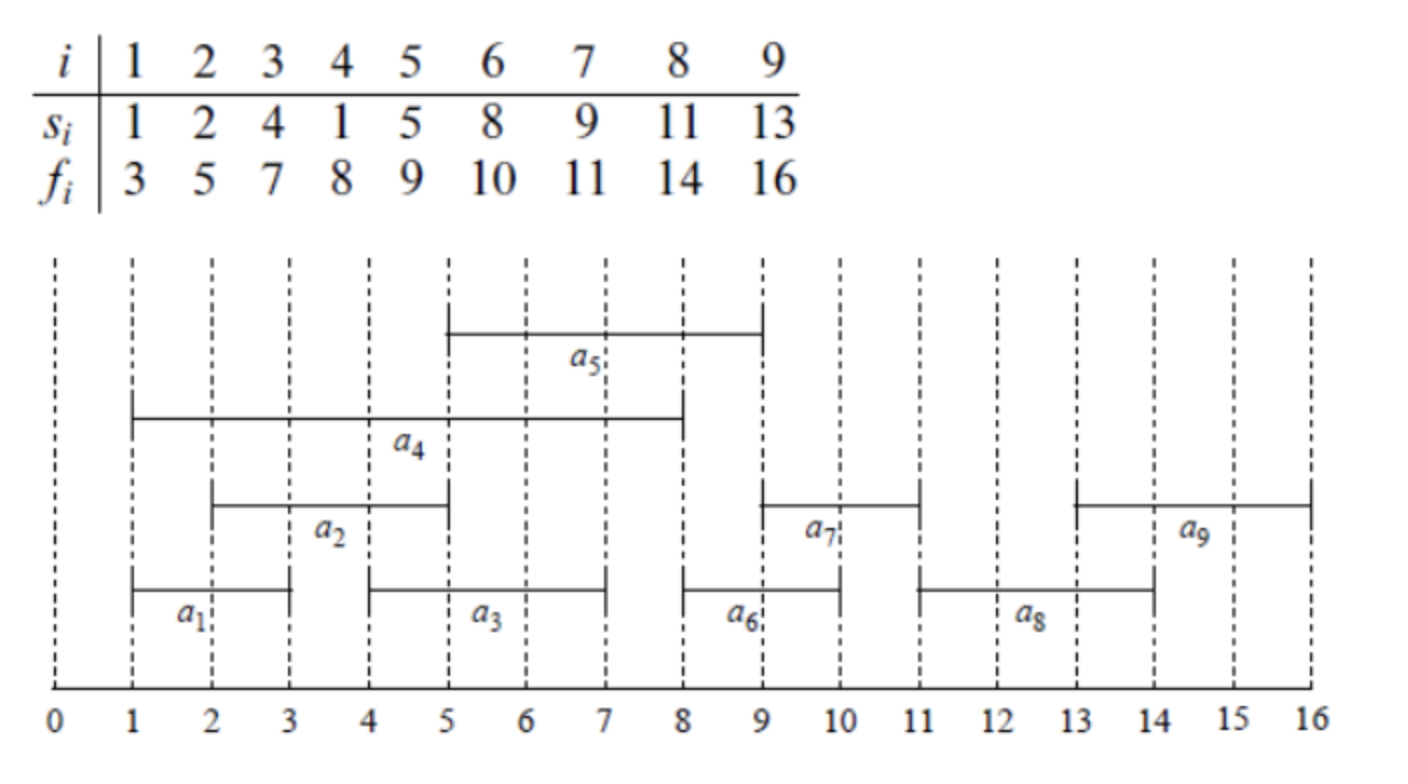
하나의 활동만 처리할 수 있는 하나의 강의실에서 제안된 활동들 중 가장 많은 활동을 처리할 수 있는 스케줄을 짜는 문제
- Si : 시작시간
- Fi : 종료시간
- 같은 강의실을 사용해야 하므로 a1과 a4는 동시에 선택 불가능
풀이
최적의 해를 구하기 위해서는 첫 번째 활동이 최대한 일찍 끝나야 함 (그래야 다른 활동들을 더 많이 선택할 수 있기 때문)
위의 경우에서는 첫 선택으로 가장 빨리 끝나는 a1 선택 --> a2와 a4는 a1과 겹치기 때문에 선택 불가능
그 이후의 선택은 다음으로 일찍 끝나는 a3 --> a6 --> a8
2. 분할 가능 배낭 문제
무게 제한이 50인 배낭에 다음과 같은 세 개의 물건을 넣는 문제 / 물건이 무거울 경우 쪼개서 넣을 수 있음
넣은 물건들의 가치(v) 합이 최대가 되어야 함
- Vi : 물건의 가치
- Wi : 물건의 무게

풀이
무게 대비 가치가 높은 것들을 먼저 넣는 것이 좋음
위의 경우에서 무게 대비 가치는 1 > 2 > 3
1번 물건을 먼저 선택 --> 2번 --> 3번 순으로 배낭에 넣기 (무게 초과인 경우는 쪼개서 넣으면 됨)
3. 거스름돈 문제
어떤 금액에 대한 거스름돈을 받고자 할 때 동전을 최소 갯수로 받게 하는 문제
각각의 거스름돈이 서로의 배수/약수 관계일 때 한정
대부분의 화폐는 배수/약수 관계이므로 탐욕 알고리즘으로 해결 가능
화폐가 배수 / 약수 관계가 아닌 경우
문제 ) 동전의 종류는 10원, 7원, 1원, 거스름돈이 14원 일 때 최적의 해는?
- 최적의 해 : 7원 2개 --> 2개
- 탐욕 알고리즘 : 10원 1개, 1원 4개를 --> 5개
매트로이드
- 탐욕 알고리즘이 언제나 최적해를 찾아낼 수 있는 구조
- 일차 독립의 성질을 공리화하여 얻은 조합론적 구조
탐욕 알고리즘 vs 동적 계획법
동적 계획법
- 문제를 여러 개의 하위 문제(subproblem)로 나누어 푼 다음, 그것을 결합하여 최종적인 목적에 도달하는 것
- 동적 계획법은 문제를 해결하기 위한 모든 방법을 검토하고 그 중에 최적의 풀이법을 찾아냄
결과에 대한 효율
탐욕 알고리즘 < 동적 계획법
시간에 대한 효율
탐욕 알고리즘 > 동적 계획법