분할정복은 너무 어려워

나의 분할정복 첫문제

문제

시간 제한	메모리 제한	제출	정답	맞힌 사람	정답 비율
0.5 초 (추가 시간 없음)	128 MB	122665	34519	25129	27.103%

문제 설명

자연수 A를 B번 곱한 수를 알고 싶다. 단 구하려는 수가 매우 커질 수 있으므로 이를 C로 나눈 나머지를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 A, B, C가 빈 칸을 사이에 두고 순서대로 주어진다. A, B, C는 모두 2,147,483,647 이하의 자연수이다.

출력

첫째 줄에 A를 B번 곱한 수를 C로 나눈 나머지를 출력한다.

예제 입력 1

10 11 12

예제 출력 1

4

---

내 풀이

이 문제를 풀기 위해선 나머지 분배 법칙과 지수법칙을 알아야 한다.

지수법칙: A^(m+n) = A^m * A^n

나머지 분배 법칙: (A*B)%C = (A%C)*(B%C)%C

# 1629 실버1
# 곱셈 
import sys
input = sys.stdin.readline

a, b, c = map(int, input().split())

def num(a,b,c):
    if b == 1:
        return a % c
    elif b % 2 == 0: # b가 짝수라면
        return (num(a,b//2,c)**2) % c
    else: #b가 홀수라면
        return ((num(a,b//2,c)**2) * a) % c

print(num(a,b,c))

아래의 식을 활용해 위의 코드를 작성했다.

기본적인 재귀함수도 아니고 재귀함수의 응용인 분할정복은 넘나 어려웠다 ...

내가 참고한 블로그

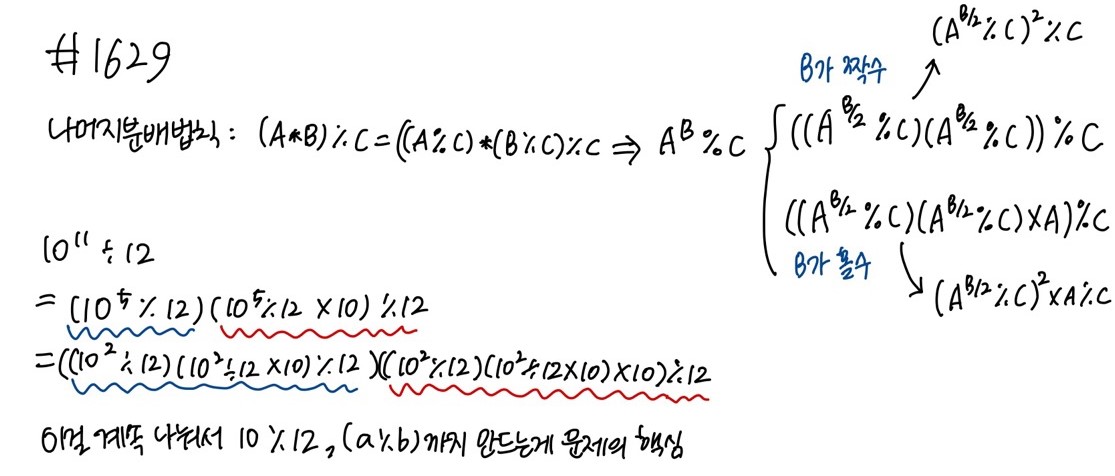
이 분의 블로그에 해당 내용이 굉장히 상세하게 정리되어 있어 이해하는데 수월했다. 감사합니당 ㅎㅎ

---

재귀함수를 사용하지 않은, 분할 정복의 개념을 활용한 거듭제곱 계산

# 분할정복 활용법을 몰라 구글링해보았다.
a, b, c = map(int, input().split())
table = [a]
for i in range(1,10):
    table.append(table[i-1]*table[i-1]) # 테이블안에 n의 1승부터 n^2, n^4, n^8 ...

result = 1 # 초기값 설정
i = 0 # 지수값 
n = # 구하려는 거듭제곱의 지수

while n > 0:
    if n%2 == 1: # n이 짝수이면 홀수가 나올때까지 2로 나눠줌
        result *= table[i] 
    n = n//2 # n이 만약 100이라면, 100 -> 25(홀수) 될때까지 2를 2번 나눠줌, 이때 i==2, result에 table[2]만큼 곱해줌
    i += 1

n이 100일 경우: 100->50->25(table[2])->12->6->3(table[5])->1(table[6])

table을 곱한 result를 계산하면 n^4 * n^32 * n^64로 n^100을 계산할 수 있다.

이런식으로 단순히 i를 n번 곱셈하는 방식이 아닌 분할정복 방식으로 시간의 효율성을 추구할 수 있다.