FHE (Fully Homomorphic Encryption)
1. FHE란?
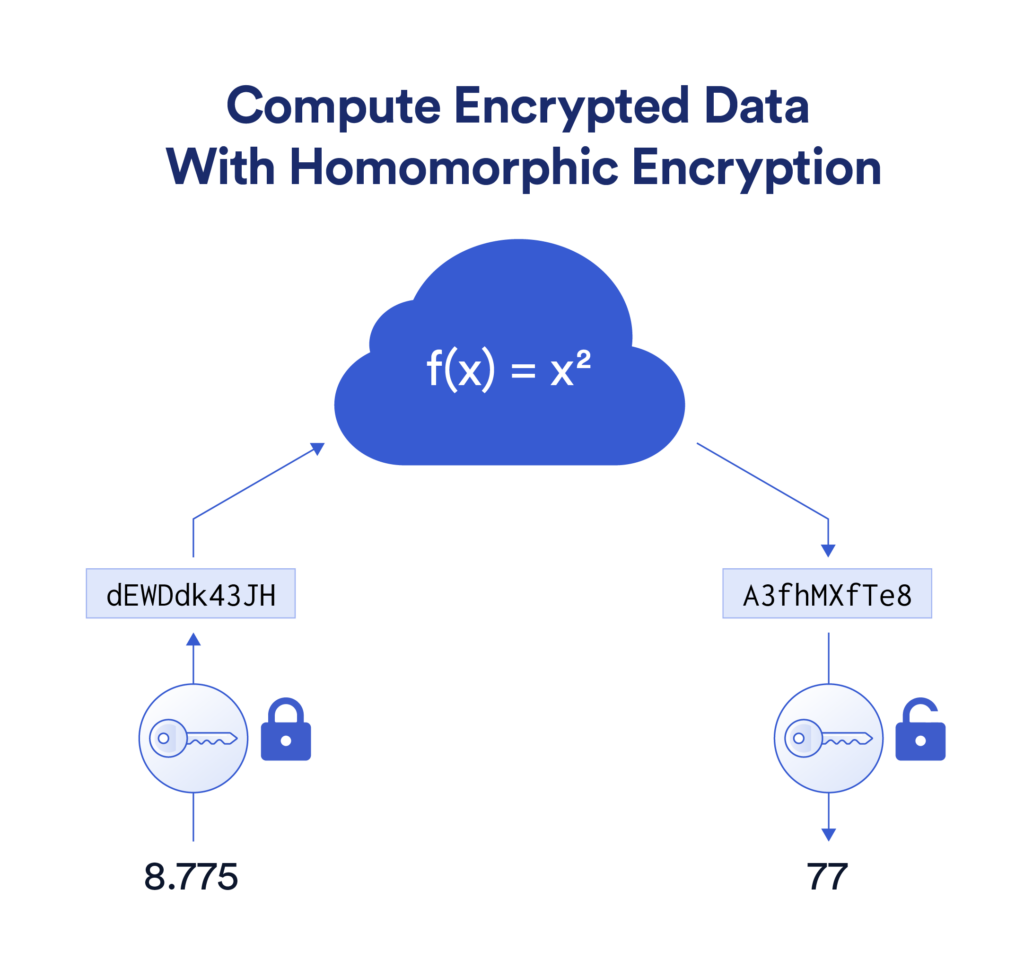
FHE, 완전 동형 암호화는 데이터가 암호화된 상태에서도 계산이 가능하도록 하는 암호화 기술이다. 이는 데이터를 복호화하지 않고도 연산을 수행할 수 있다. 즉, 데이터의 기밀성을 유지하면서 계산을 처리할 수 있게 해준다.
동형 암호화는 크게 세 가지로 나뉜다. 1. 덧셈 동형 암호화 2. 곱셈 동형 암호화 3. 완전 동형 암호화
- 덧셈 동형 암호화: 암호문 상태에서 덧셈 연산을 수행 가능
- 곱셈 동형 암호화: 암호문 상태에서 곱셈 연산을 수행 가능
- 완전 동형 암호화: 암호문 상태에서 덧셈과 곱셈 모두 수행 가능,
두 연산의 조합으로 이루어진 복잡한 계산도 가능.
완전 동형 암호화는 수십 년동안 암호학자들이 고민하던 주제였으나, 2009년 Craig Gentry의 초기 논문에서 제안된 'bootstrapping' 과정을 통해 실제로 구현가능해졌다.
bootstrapping의 핵심 아이디어는 암호문에 대해 연산을 여러 번 수행하다 보면 잡음이 커져서 복호화가 불가능해지는 문제가 발생하는데, 이를 부트스트래핑을 통해 주기적으로 잡음을 제거하여 무제한으로 연산을 수행할 수 있게 하는 것이다.
잡음이 축적되는 이유
FHE에서 사용하는 암호화 방식의 본질적인 특성에 기인한다. 이를 이해하려면 암호화된 상태에서 연산이 어떻게 이루어지는지를 살펴보아야 한다.
FHE에서 암호화는 평문을 단순한 수학적 구조로 변환하는 것이 아니라, 안전성을 보장하기 위해 랜덤 값인 '잡음'을 추가하는 과정을 포함한다. 이 잡음은 추가함으로써 평문을 직접적으로 재구성하지 못하게 방지한다.
잡음이 축적되는 문제는 동형연산(homomorphic operation)을 암호문에 반복해서 적용할 때 발생한다. FHE에서 암호화된 데이터에 대해 연산을 수행할 때, 기존 암호문에 존재하던 잡음들이 결합되어 연산 과정에서 더 커진다. 특히 곱셈 연산을 통해 잡음이 기하급수적으로 커지며, 연산이 반복될수록 계속해서 축적된다.
이는 곧 noise가 noise budget을 넘어가게 되고, 이는 원래의 평문을 정확히 복호화할 수 없게 만든다. (noise budget은 암호문에 허용되는 잡음의 최대치로, 이를 초과하면 안전한 복호화가 불가능해진다.)
보통 FHE에서 noise는 lattice- based encryption 방식에서 발생한다. 격자 기반 암호화에서는 암호문이 고차원 격자의 점들로 표현되며, noise는 이 점들 사이의 거리에 영향을 준다. 연산을 반복할 때마다 거리가 더 복잡해지고, noise가 축적되면서 결과적으로 복호화가 어려워지는 것이다.
격자 암호처럼 LWE(Learning with Errors)와 같은 문제에 기반한 암호화에서는 잡음의 크기가 보안성을 결정하는 중요한 요소로 작용한다. LWE 문제에서 잡음은 평문과 암호문 사이의 관계를 모호하게 만들어 보안성을 높이는 역할을 하지만, 연산이 진행될수록 noise가 커지기 때문에 이를 제어하는 것이 FHE의 핵심 과제가된다.
https://vitalik.eth.limo/general/2020/07/20/homomorphic.html
https://ethresear.ch/t/open-problem-improving-stealth-addresses/7438
: 스텔스 주소 프로토콜