PLONK_prover

pse core program 5주차 PLONK_prover round5 발표를 준비하며 정리해보았습니다. plonk paper와 도훈님의 https://velog.io/@dohoon8/Note-PLONK-algorithm 블로그 글을 참조하여 작성하였습니다. 업사이드 아카데미 후속지원 프로그램 ZKP 스터디를 준비하며 prover round 전 과정을 추가하였습니다.

---

1. PLONK란 무엇인가?

PLONK는 Permutation argument for LOgarithmic-size Non-interactive Knowledge의 약자로, zk-SNARK(Zero-Knowledge Succinct Non-interactive Argument of Knowledge) 프로토콜의 일종입니다.

PLONK는 기존 zk-SNARK 시스템보다 범용성을 높이기 위해 탄생하였습니다.

PLONK는 기존의 zk-SNARK 시스템처럼 개별 회로마다 신뢰 설정(trusted setup)이 필요 없습니다. 범용적이고 업데이트 가능한 신뢰 설정(Structured Reference String, SRS)를 사용한기 때문입니다. 이로 인해 회로마다 새로운 신뢰 설정을 하지 않아도 되므로, 여러 애플리케이션에 재사용할 수 있습니다.

1.1 Groth16과 Plonk의 주요 차이점

두 프로토콜 간의 가장 큰 차이점은 Trusted Setup 방식에 기인합니다. Groth16은 특정 회로에 대한 설정이 필요한 반면, plonk는 범용적이고 업데이트 가능한 설정을 사용합니다. 즉, Groth16은 증명하려는 회로 하나 하나에 맞춰 별도의 Trusted Setup을 설정해야하고, 이는 매 증명마다 달라지기에 번거롭고 비용이 많이 듭니다. 또한 Trusted Setup 시 생성되는 toxic wasted라고 불리는 비밀 값을 완전히 폐기해야합니다.

하지만 Plonk는 한 번의 Trusted Setup으로 다양한 종류의 회로를 증명할 수 있습니다. Groth16은 작은 증명 크기와 검증 속도 등 성능을 극대화해야 하는 특정 상황에서 유리하고, Plonk는 유연성과 재사용성이 중요하고 다양한 증명을 필요로 하는 상황에 훨씬 더 실용적이고 편리한 방식입니다.

1.2 Plonk paper Abstraction

업데이트 가능한 범용 구조화된 참조 문자열(universal structured reference string)을 활용하는 zk-SNARK 구조는 zk-SNARK 배포의 주요 장애물 중 하나를 제거합니다. Maller 등의 중요한 연구([MBKM])는 이러한 SRS(Structured Reference String)를 사용하여 일반적인 산술 회로에 대해 완전하고 간결한 검증이 가능한 최초의 실용적인 zk-SNARK인 Sonic을 제시했습니다. 하지만 Sonic에서 완전하고 간결한 검증을 가능하게 하는 버전은 여전히 상대적으로 높은 증명 생성 오버헤드를 필요로 합니다.

우리는 완전하고 간결한 검증이 가능하면서도 증명자(prover)의 실행 시간을 훨씬 단축시킨 (회로 구조에 따라 [MBKM]보다 약 7.5배에서 20배 적은 그룹 지수 연산) 범용 SNARK 구조를 제시합니다.

[MBKM]과 유사하게, 우리는 Bayer와 Groth [BG12]에 기반한 순열 인자(permutation argument)에 의존합니다. 그러나 우리는 "단항식의 계수(coefficients of monomials)"가 아닌 "부분 그룹에 대한 평가(Evaluations on a subgroup)"에 초점을 맞춥니다. 이를 통해 순열 인자와 산술화(arithmetization) 단계를 모두 단순화할 수 있습니다.

2. PLONK의 핵심 구조와 개념

2.1 회로 산술화 (Arithmetization)

PLONK는 계산을 다항식 시스템으로 변환합니다. 이를 회로 산술화라고 하는데, 주어진 회로를 산술적 표현으로 변환하는 과정입니다. PLONK는 단항 다항식을 사용하여 이 과정을 단순화하고 효율적으로 수행합니다.

2.2 순열 논증 (Permutation Argument)

PLONK의 순열 논증은 Bayer와 Groth의 [BG12] 논문에서 소개된 기술을 기반으로 합니다. 이 논증은 계산 과정에서 변수를 올바르게 매핑했는지를 확인하기 위한 절차입니다. 구체적으로, PLONK는 Lagrange 기반을 사용하여 다항식의 특정 지점에서의 값을 확인하는 방식으로 이를 간단하게 만듭니다.

2.3 SRS와 증명 구조

PLONK는 업데이트 가능한 신뢰 설정(SRS)을 사용합니다. SRS는 계산의 보안을 보장하는 데 필요한 데이터로, 모든 회로에서 동일하게 사용할 수 있습니다. 이는 기존 zk-SNARK 시스템에서 각 회로마다 새로운 신뢰 설정을 필요로 했던 점과 비교했을 때 큰 장점입니다.

---

Plonk_Prover_Preprocessing

PLONK 증명을 생성하기 전에, 우리가 증명하고자 하는 복잡한 계산 회로(Circuit)를 PLONK가 이해할 수 있는 형태로 변환하는 과정이 필요합니다.

덧셈, 곱셈 등의 모든 게이트를 아래와 같은 표준 게이트 제약(Standard Gate Constraint)이라는 단일 공식으로 표현합니다.

• $a_i, b_i$: i번째 게이트의 왼쪽, 오른쪽 입력 값
• $c_i$: i번째 게이트의 출력 값
• $q_{L,i}, q_{R,i}, q_{M,i}, q_{O,i}, q_{C,i}$: 게이트의 종류를 결정하는 셀렉터(selector) 다항식의 i번째 값

또한, 회로 내에서 어떤 와이어가 어떤 와이어와 연결되는지에 대한 정보(Copy Constraints)를 순열(Permutation) $\sigma$로 정의합니다.

본격적으로 Prover의 5round에 대해 알아보겠습니다.

Plonk_Prover_Round 1

- Wire Polynomial Commitment 생성

prover는 n개의 게이트에 대한 witness를 사용하여 회로의 각 와이어(left, right, output)에 해당하는 다항식 형태로 변환하고, 이를 commit하여 검증자에게 전달합니다.

1. 증명자는 회로의 왼쪽, 오른쪽, 출력 와이어에 해당하는 값들 $(a_i, b_i, c_i)_{i=1}^n$을 보간(interpolate)하여 세 개의 Wire polynomial) $a(X), b(X), c(X)$를 만듭니다. wire polynomial $a(X), b(X), c(X)$ 를 다음과 같이 계산합니다.

   $\begin{aligned} a(X) = (b_1X + b_2)Z_H(X) + \sum_{i=1}^nw_iL_i(X) \\ b(X) = (b_3X + b_4)Z_H(X) + \sum_{i=1}^nw_{n+i}L_i(X) \\ c(X) = (b_5X + b_6)Z_H(X) + \sum_{i=1}^nw_{2n+i}L_i(X) \end{aligned}$

2. 영지식을 위해, 랜덤한 블라인딩 스칼라 $b_1, ..., b_6 \in \mathbb{F}$를 선택합니다.

3. 이 랜덤 값들을 이용해 블라인딩 다항식을 만든 뒤, 원래의 증명 다항식에 더해줍니다. 이 때 소멸 다항식(vanishing polynomial) $Z_H(X) = X^n -1$ 을 곱해줍니다. $Z_H(X)$는 우리가 관심 있는 영역(도메인 H)에서는 값이 0이므로, 이 항을 더해도 원래 증명의 유효성(soundness)에는 영향을 주지 않으면서 다항식 전체는 랜덤화됩니다.

   $a(X) := (b_1X + b_2)Z_H(X) + a_{wit}(X)$
   $b(X) := (b_3X + b_4)Z_H(X) + b_{wit}(X)$
   $c(X) := (b_5X + b_6)Z_H(X) + c_{wit}(X)$

4. 이렇게 블라인딩 처리된 최종 다항식들을 Kate-Zaverucha-Goldberg (KZG) 다항식 커밋먼트 스킴을 사용하여 커밋합니다. 즉, 신뢰할 수 있는 설정(SRS) 값 $[s^i]_1$을 이용해 아래의 커밋먼트를 계산합니다.

   $[a] := [a(s)]_1, \quad [b] := [b(s)]_1, \quad [c] := [c(s)]_1$

최종적으로 블라인딩 처리된 증명 다항식의 커밋먼트 $[a], [b], [c]$를 verifier에게 보냅니다.

Plonk_Prover_Round 2

- Permutation Polynomial Commitment 생성

모든 와이어들이 올바르게 연결되었다는 제약(copy constraint)을 단일 다항식 $Z(X)$으로 압축하고, 이 다항식을 블라인딩 처리하여 커밋합니다.

1. Trascript로부터 랜덤한 챌린지 값 $\beta, \gamma \in \mathbb{F}$를 받습니다. (비대화형에서는 이전 결과들을 해시하여 생성)
2. 이 값들을 이용해 모든 와이어 연결 정보를 담고 있는 순열 다항식(permutation polynomial) $Z(X)$를 구성합니다. 이 다항식은 "누적 곱(running product)" 방식으로 만들어지며 모든 와이어 연결이 올바른지를 확인하는 역할을 하게 됩니다.

먼저 다음과 같은 permutation polynomial $z(X)$를 계산합니다.

첫번째 줄은 [[PLONK - Round 2|Round2]]과 마찬가지로 영지식성을 위해 추가된 부분입니다. 두번째 줄과 세번째 줄은 [[(Extended) Polynomial Protocol For Identifying Permutations|permutation check]] 에서 $Z(X)$가 만들어지는 과정을 약간 변형한 것입니다. 기본적으로 $X=\omega$에서 1, 그 이후로는 누적 곱이 되는 induction 형태만 조금 다르고 과정은 동일합니다

여기서, $Z(X)$의 시작점은 $Z(g_1) = 1$로 정의합니다. 이후 $i = 1, \dots, n$에 대해, 다음과 같은 재귀적인 관계로 $Z(g_{i+1})$ 값을 계산하여 $Z(X)$를 구성합니다.

이 수식은 두 다중집합이 서로의 순열 관계인지 확인하는 과정입니다.

분자: $i$번째 게이트에 연결된 각 와이어의 값($a_i, b_i, c_i$)과, 그 와이어의 고유한 위치 식별자($g_i, k_1 g_i, k_2 g_i$)를 $\beta, \gamma$와 결합하여 하나의 항으로 만듭니다. 분자 전체의 곱은 모든 와이어의 값, 위치 정보를 나타내는 다중집합을 표현합니다.

분모: $i$번째 게이트에서 각 와이어의 값을 permutation에 의해 연결될 위치의 식별자, $S_{\sigma_1}(g_i), S_{\sigma_2}(g_i), S_{\sigma_3}(g_i)$와 결합합니다.분모 전체의 곱은 모든 와이어의 값, 연결될 위치 정보를 나타내는 또 다른 다중집합을 표현합니다. 즉, $i$번째 와이어가 연결될 위치를 알려줍니다.

만약 모든 copy constraint가 만족된다면, 분자에 있는 모든 항의 다중집합과 분모에 있는 모든 항의 다중 집합은 순서만 다를 뿐 정확히 동일합니다. 따라서 누적 곱을 계속해 나가면 분자와 분모가 서로 상쇄되어 최종적으로 $Z(g_{n+1})=1$이 됩니다. (Schwartz-Zippel 보조정리에 기반한 확률적 검증 방법)

3. Round 1과 마찬가지로, 영지식을 위해 랜덤 스칼라 $b_7, b_8, b_9$를 선택하고 소멸 다항식 $Z_H(X)$를 이용해 $Z(X)$를 블라인딩 처리합니다.

   $Z(X) \leftarrow Z(X) + (b_7X^2 + b_8X + b_9)Z_H(X)$

4. 블라인딩 처리된 최종 순열 다항식 $Z(X)$를 KZG 스킴으로 커밋합니다.

   $[Z] := [Z(s)]_1$

계산된 커밋먼트 [Z]를 검증자에게 보냅니다.

Plonk_Prover_Round 3

몫 다항식 커밋먼트 (Quotient Polynomial Commitment)

지금까지의 모든 gate constraint와 copy constraint를 단일 다항식으로 통합하고, 이 다항식이 전체 회로에서 유효함을 증명하는 몫 다항식$t(X)$를 생성하여 커밋합니다.

1. Transcript로부터 또 다른 랜덤 챌린지 값 $\alpha \in \mathbb{F}$ 를 받습니다.

2. 증명자는 이 $\alpha$를 가중치처럼 사용하여, 회로의 모든 제약 조건을 만족할 때만 $0$이 되는 거대한 단일 방정식을 만듭니다. 이 방정식이 모든 게이트에서 성립한다면, 반드시 소멸 다항식(vanishing polynomial) $Z_H(X) = X^n - 1$으로 나누어 떨어집니다. 이 나눗셈의 결과를 몫 다항식 $t(X)$ 라고 합니다.

   $t(X) = \frac{f(X)}{Z_H(X)}$

   여기서 분자 $f(X)$는 다음과 같이 구성됩니다.
   $f(X) = \text{(Gate Constraint)} + \alpha \cdot \text{(Permutation Constraint)} + \alpha^2 \cdot \text{(Permutation Constraint)}$

   1) Gate Constraints:
   $a(X)q_L(X) + b(X)q_R(X) + a(X)b(X)q_M(X) + c(X)q_O(X) + PI(X) + q_C(X)$

   2) Permutation Constraints:
   $(a(X)+\beta X+\gamma)(b(X)+\beta k_1 X+\gamma)(c(X)+\beta k_2 X+\gamma)Z(X) \\ - (a(X)+\beta S_{\sigma_1}(X)+\gamma)(b(X)+\beta S_{\sigma_2}(X)+\gamma)(c(X)+\beta S_{\sigma_3}(X)+\gamma)Z(X\omega)$

   3) Permutation Start Constraints:
   $L_1(X)(Z(X)-1)$

3. 이렇게 계산된 $t(X)$는 차수가 매우 높기 때문에($3n$ 이상), 효율적인 처리를 위해 이를 $n-1$차 다항식 세 개로 분할합니다.

   일차항은 $Z(X)$가 multiplicative subgroup 위에서 어떻게 정의되는지를 나타내며, 이차항은 $Z(\omega)=1$, 즉 copy constraint가 만족해야 함을 나타낸다. Plonk에서 check 하려는 모든 조건이 담겨 있는 다항식임을 알 수 있다. $t(X)$의 degree가 최대 3n+5일 수 있는데 srs에는 $x^{n+5}$까지만 준비돼 있기 때문에, $t(X)$를 다음과 같이 표현한다.
   -dohoon8

   $t(X) = t_{lo}(X) + X^n t_{mid}(X) + X^{2n} t_{hi}(X)$

4. 분할된 세 개의 몫 다항식을 각각 KZG 스킴으로 커밋합니다.

   $[t_{lo}] := [t_{lo}(s)]_1, \quad [t_{mid}] := [t_{mid}(s)]_1, \quad [t_{hi}] := [t_{hi}(s)]_1$

분할된 몫 다항식들의 커밋먼트 [t_lo], [t_mid], [t_hi]를 검증자에게 보냅니다.

Plonk_Prover_Round 4

Polynomial Evaluation

검증자가 지정한 임의의 지점에서 evaluate 합니다. 지금까지의 커밋먼트들이 실제로 올바른 다항식으로부터 생성되었음을 보일 준비를 하는 것입니다.

1. Transcript로부터 랜덤한 평가 지점 $ζ \in \mathbb{F}$를 받습니다.
2. 증명자는 이 $z$에서 다음 다항식들의 값을 계산하여 검증자에게 전송합니다.
   • $a(ζ), b(ζ), c(ζ)$ : 세 개의 wire 다항식
   • $S_{\sigma1}(ζ), S_{\sigma2}(ζ)$ : 두 개의 permutation 다항식
   • $Z(z\omega)$ : permutation constrain 검증에 필요한 $Z(X)$다항식은 ζ의 shifted point인 $ζw$에서 평가합니다.

$z$와 $z\omega$ 지점에서의 각 다항식 평가 값(evaluation)들을 $(\bar{a}, \bar{b}, \bar{c}, \bar{s}{\sigma1}, \bar{s}{\sigma2}, \bar{ζ}_{\omega})$을 검증자에게 보냅니다. 검증자에게 보냅니다.

PLONK_Prover_Round 5

PLONK paper에서 PLONK의 과정을 arithmetization, Prover round1-5, Verifier으로 나누어 설명합니다. 본문에서는 PLONK의 prover 과정 중 round5에 대해서 집중적으로 기술합니다.

SNARK Relation
: public input과 prover가 제공한 증명(witness)간의 관계를 정의하는 역할

$R$: SNARK 관계를 나타내는 기호입니다. 이는 특정 집합의 관계를 나타내며, 증명자가 제공한 증명(witness)와 공개 입력(public input) 간의 관계를 규정합니다.

$𝐹^𝑙$: 이는 필드 𝐹위의 벡터 공간을 의미합니다. 여기서
𝑙은 공개 입력 값들의 개수를 나타냅니다. 즉, $𝐹^𝑙$는 𝑙개의 public input을 담고 있는 공간입니다.

$F^{3n−l}$: 이는 필드 𝐹위의 또 다른 벡터 공간을 의미하며, 3𝑛−𝑙개의 요소를 가진 벡터 공간입니다. 이 공간은 주로 증명자가 제공한 witness 값들을 포함합니다. 여기서 𝑛 은 회로의 크기를 의미하며, 증명에 필요한 중간 결과 값(witness)의 개수는 총 3𝑛−𝑙이 됩니다.

공개 입력과 witness 값 정의

𝑙: 공개 입력의 개수를 나타내는 변수입니다. 회로의 일부 입력 값들이 공개될 때, 그 값들이 𝑙개라는 의미입니다.

3𝑛−𝑙: 회로에서 생성되는 witness 값의 개수입니다. 여기서 𝑛은 회로의 크기(게이트의 개수 등)로 결정됩니다.

따라서 public input은 회로의 일부가 외부에서 주어지는 값이며, witness 값은 회로 내에서 계산된 중간 결과 값들입니다.

$z(X)$는 copy constraint를 만족함을 증명하는 다항식,
$t(X)$는 gate constraint와 copy constraint를 만족하는지 검사하기 위한 quotient polynomial입니다.

$z_H(X)$는 도메인 H위의 루트 다항식입니다. H = {1, $w$, $w^2$,,,$w^{n-1}$}라면, 이 부분군의 각 원소에서 0이되는 다항식입니다.
$z_H(X)$ = $(X-1)(X-w)(X-w^2)(X-w^{n-1})$
여기서 $w$는 생성자로써, 도메인 $H$의 각 원소는 이 생성자의 거듭제곱입니다.

$t(X)$는 다음과 같이 계산 됩니다.

분자에 있는 복잡한 다항식을 $p(X)$라고 할 때,
$t(X)$= $p(X)/Z_H(X)$ 형태입니다.
prover가 $q(X)$를 알고 있음을 증명하기 위해서는 evaluation challenge에서 $t(X)$, $Z_H(X)$, $p(X)$를 각각 계산한 값들을 전달해야 합니다.

PLONK paper에서는 Prover가 전달해야 하는 field element의 개수를 줄이기 위해서 'linearisation polynomial'을 만듭니다.

Round5: 선형화 다항식 계산 및 최종 평가

• 증명자는 여러 다항식을 하나로 결합한 선형화 다항식 $r(X)$를 계산합니다.
• 또한, 최종 증명 값으로 첫 번째 Opening Proof $W_ζ(X)$와 두 번째 Opening Proof $W_{ζω}(X)$를 생성하여 검증자에게 제공합니다.

Round5의 Output은 Opening Proof Polynomial에 대한 commitment인 $[W_ζ]_1$, $[W_{ζω}]_1$입니다.

결국 증명자는 회로 내에서 gate constraint와 copy constraint를 만족한다는 사실을 검증자가 확인할 수 있도록 여러 단계의 다항식 계산과 평가를 수행합니다.

linearisation polynomial는 다음과 같습니다.

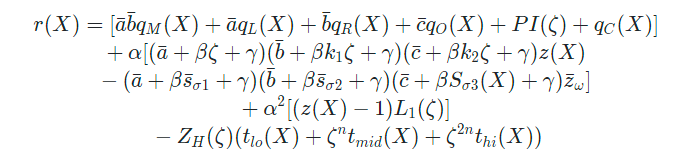
$t(X)$= $p(X)/Z_H(X)$ 형태를 $r(X)$ = $p(X)$ - $t(X)$$Z_H(X)$ 형태로 바꾼 것입니다.
이러면 element들에 대해 각각의 evaluation proof가 아닌 단일 $r(ζ)$ = 0에 대한 proof만 생성하면 됩니다.

아래는 Plonk Paper의 라운드 5 과정을 전부 설명한 것이고, 3번부터 보셔도 무방합니다.

1. Opening Challenge $v$계산

• 먼저 Opening Challenge $v$를 계산해봅시다. 이 값은 필드 $F$위에서 선택되며, 이는 $H$(transcript)를 사용해 무작위로 생성됩니다.

• 여기서 $H$는 해시함수로, transcript(이전에 발생한 모든 데이터 기록)을 입력으로 받아 무작위 값을 생성합니다.
  Plonk paper에는 해시함수가 명시되어 있지 않지만, 보통 SHA-256 혹은 포세이돈 함수를 사용합니다.

• $v = H(transcript)$

이$v$는 이후의 여러 다항식들의 결합 과정에서 사용됩니다.

2. 선형화 다항식 $r(X)$계산

• 선형화 다항식 $r(X)$는 여러 다항식들을 결합하여 하나의 단일 다항식으로 만드는 과정입니다.
• 이 선형화 다항식은 이전 라운드에서 계산된 다양한 다항식들, 즉 $q_M(X)$, $q_L(X)$, $q_R(X)$, $q_O(X)$와 같은 선택자 다항식들과, 평가된 값들 $\bar{a}, \bar{b}, \bar{c}$, 순열 관련 다항식들 $\bar{S}_{\sigma 1}, \bar{S}_{\sigma 2}, \bar{z}_{\omega}$ 등을 사용해 구성됩니다.

3. 첫 번째 Opening Proof Polynomial $W_ζ(X)$계산

• 첫 번째로 계산하는 Opening Proof Polynomial은 $W_ζ(X)$입니다. 이는 여러 다항식들의 무작위 선형 결합입니다.

• 각 다항식은 특정 평가 지점인 $ζ$에서 평가된 값들과 결합됩니다.

  $W_{\zeta}(X) = \frac{1}{X - ζ} \left( r(X) + v(a(X) - \bar{a}) + v^2(b(X) - \bar{b}) + v^3(c(X) - \bar{c}) + v^4(S_{\sigma1}(X) - \bar{S}_{\sigma1}) + v^5(S_{\sigma2}(X) - \bar{S}_{\sigma2}) \right)$

  $ζ$ '제타'라고 불리는 무작위 평가점은 증명자가 transcript를 해시하여 생성한 값으로, 검증자가 선택한 것 처럼 행동하지만, 실제로는 증명자가 만든 것입니다.
  $v$ 해당 값 또한 transcript를 해시하여 만든 값으로, 다항식 결합에 있어 무작위성을 추가하여 부정행위 가능성을 줄이고 증명자의 신뢰성을 높이는 데 사용합니다.

• 이 식은 여러 다항식을 제타에서 evaluation하고, 그 결과를 하나로 결합한 형태입니다.

• v는 앞서 말했듯이 계산한 무작위 challenge 값으로, 다항식을 결합하는 데 사용됩니다.

4. 두 번째 Opening Proof Polynomial $W_{ζω}(X)$계산

• 이는 copy constraint와 관련된 다항식입니다.
  $W_{\zeta \omega}(X) = \frac{z(X) - \bar{z}_{\omega}}{X - \zeta \omega}$
• 여기서 $z(X)$는 copy constraint를 나타내는 다항식이고, $\bar{z}_{\omega}$는 이 다항식이 평가된 값입니다. $ζω$ 또한 무작위 평가점입니다.
• 왜 Opening Proof Polynomial에 ζ와 그 이웃점인 ζω가 필요하나? => Plonk에서는 copy constraint를 한 칸씩 전진하며 점검하는데, 현재점 ζ에서의 관계가 다음점 ζω에서도 맞는지 확인해야 하기에 두 곳에서 값을 열어보는 절차가 필요한 것입니다.
• 이 다항식은copy constraint가 올바르게 성립하는지 확인하기 위해 사용됩니다.
  Plonk Prover Algorithm의 최종 결과는 아래와 같습니다.

5. Commitment 계산

• 이 두개의 Opening Proof Polynomial에 대한 commitment를 계산합니다.
• $[W_ζ]_1$와 $[W_{ζω}]_1$는 각각 $W_ζ$, $W_{ζω}$에 대한 commitment를 나타냅니다.
• 이 commitment들은 검증자가 증명자에게 제공한 다항식들이 올바르게 평가되었는지를 확인하는 데 사용딥니다.

6. 최종 증명 $\pi_{\text{SNARK}}$ 반환

$\pi_{\text{SNARK}} = \left( [a]_1, [b]_1, [c]_1, [z]_1, [t_{\text{lo}}]_1, [t_{\text{mid}}]_1, [t_{\text{hi}}]_1, \bar{a}, \bar{b}, \bar{c}, \bar{S}_{\sigma 1}, \bar{S}_{\sigma 2}, \bar{z}_{\omega}, [W_{\zeta}]_1, [W_{\zeta \omega}]_1 \right)$