통계학도감(3) - 추측통계학

목차

3.1 표본으로 모집단의 특성을 파악한다.
3.2 모수를 잘 대입한다 : 불편추정
3.3 제약을 받지 않는 데이터의 수 : 자유도
3.4 표본통계량의 분포_1: 평균의분포
3.5 표본통계량의 분포_2: 비율의분포
3.6 표본통계량의 분포_3: 분산의분포
3.7 표본통계량의 분포_4: 상관계수의분포
3.8 측정값과 참값의 차이 : 계통오차와 우연오차
3.9 표본평균에 관한 두 정리 : 대수의 법칙과 중심극한정리

3.1 표본으로 모집단의 특성을 파악한다 :

• 추측통계학 : 표본을 사용해 그 추출원인 모집단의 특징(모수)을 추측한다.
  

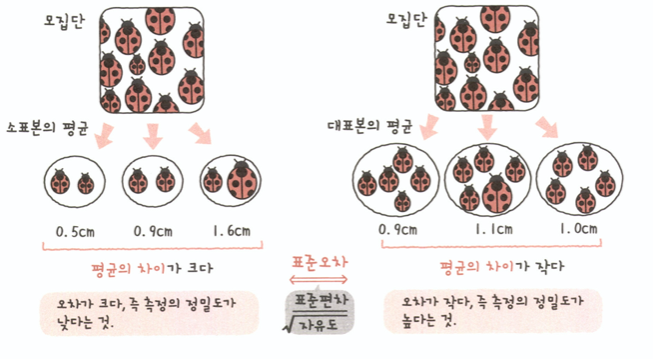
• 대표본과 소표본 : 보통 30개 미만은 소표본. 소표본은 추측의 정도가 낮아지며, 검정 등이 잘못될 가능성이 있다.(소표본의 문제)

3.2 모수를 잘 대입한다 : 불편추정

• 불편추정이란 참값인 모수와 비교해 큰 쪽에도 작은 쪽에도 치우지지 않은 통계량을 표본에서 추정하는 것을 말한다.
• 기술통계학 방법으로 통계량을 계산하면 참값인 모수보다 커지기도 하고 작아지기도 한다. 이런 치우침을 수정한 통계량(불편추정량)을 얻는 것이 불편추정이다.

• 해당 부분이 잘 이해가 되지 않아, 실험해봄. 1~10까지 값으로 표본분산과 모분산을 구해보면 값이 다르다. 이는 자유도에 의한 차이.
• (아래 양측 분모n을 n+1로 수정.)
  

• 불편추정 수정방법
  

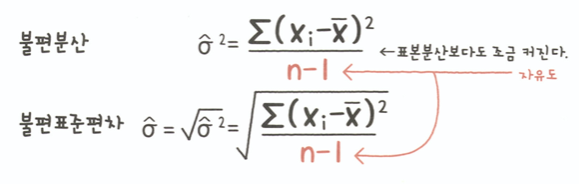
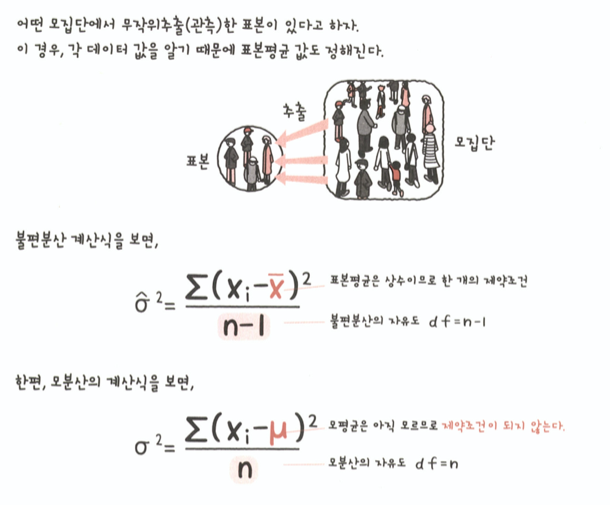
• 표본의 정보만을 이용해, 모수에 대해 치우침이 없도록 추정하는 통계량.

• 그리스 문자 ^(햇)을 써서 구별한다.

• 평균은 모평균보다 커질지 작아질지 모르기 때문에 수정할 수 없어 표본평균 그대로 불평평균으로 생각한다.

3.3 제약을 받지 않는 데이터의 수 : 자유도(Degree of Freedom. df)

• 자유도 : 통계량 계산에 사용하는 관측 데이터 중, 자유롭게 값을 취할 수 있는 데이터의 수를 말한다. 표본 크기에서 제약 조건의 수를 뺀 값이 자유도의 크기이다. (제약조건수는 계산식의 수)

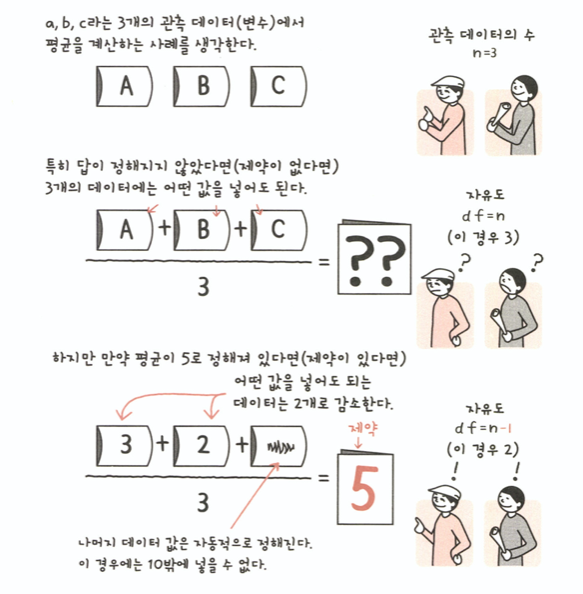
• 표본에서 평균 등을 계산할 때마다 자유도가 하나씩 감소한다.
  

3.4 표본통계량의 분포_1: 평균의분포

• 개별 관측 데이터뿐 아니라 표본통계량도 확률분포를 따른다.
• 표본분포
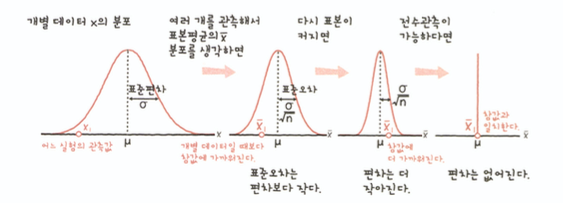
  - 표본은 여러번 추출할 수 있다. 그리고 이들 통계량의 값은 다르기 떄문에 불규칙한 분포를 보인다.
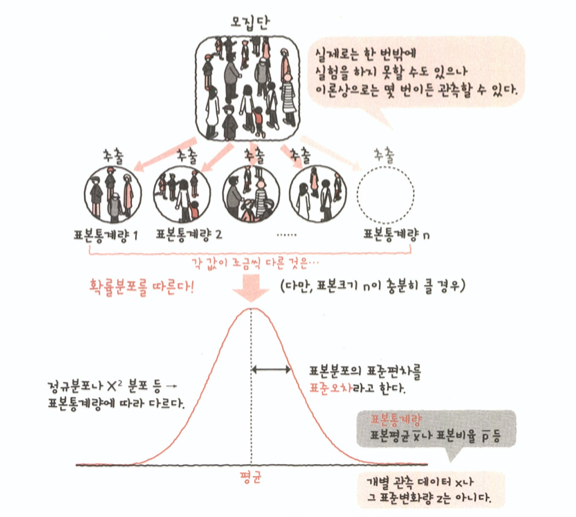
  • 표본분포의 불규칙한 분포크기(표준편차)를 표준오차라고 하고, 오차 범위를 예측하는 데 사용한다.
    

• 표본평균의 분포는 정규분포를 따른다.
• 표준화된 표본평균의 분포는 z분포를 따른다.
• 표준화된 표본평균의 분포는 t분포를 따른다. : 모분산을 알 수 없기 때문에 불편표준오차로 스튜던트화한 표본평균은 t분포를 따른다.

3.5 표본통계량의 분포_2: 비율의분포

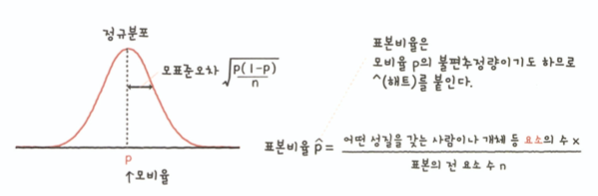
• 표본비율은 '어떤 성질을 갖는 요소의 수 x'는 이항분포를 따른다.
• 표본비율도 표본크기가 커지면 정규분포를 따른다.
  

3.6 표본통계량의 분포_3: 분산의분포

• 표본분산이 따르는 확률분포는 없으므로, 카이제곱 분포를 따르도록 표분분산, 또는 불편분산과 비례하는 통계량으로 변혼한다.
• 모분산의 구간추정이나 검정에서 이용한다.

3.7 표본통계량의 분포_4: 상관계수의분포

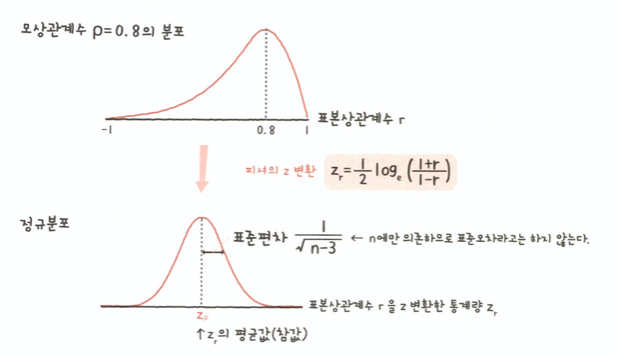
• 모상관계수가 0이 아닌 경우, 표본상관계수 r은 기울어진 분포를 따르기 때문에 그대로 사용할 수 없다.
• 피셔의 z변환을 하면 정규분포를 따르기 때문에, 모상관계수의 신뢰구간 추정으로 사용할 수 있다.

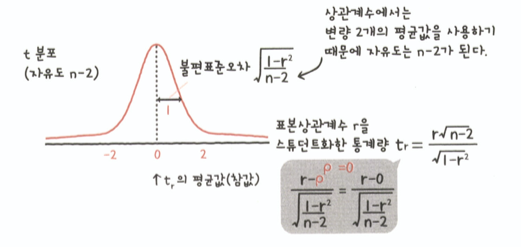
• 모상관계수가 0인 경우(즉, 무상관), 표본상관계수 r은 스튜던트화해 t분포를 따른다.
• 상관계수의 검정에 이용할 수 있다.
  

3.8 측정값과 참값의 차이 : 계통오차와 우연오차

• 오차 : 참값인 모수와 표본에서 계산된 통계량 사이에는 대게 차이가 발생. 이 차이를 오차라고 한다.
• 계통오차와 우연오차 비교
  

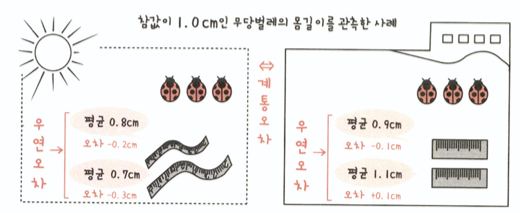
• 표준오차
  - 표준오차는 표본분포가 고르지 않은 것으로 표본평균의 우연 오차 지표이다.
  

3.9 표본평균에 관한 두 정리 : 대수의 법칙과 중심극한정리

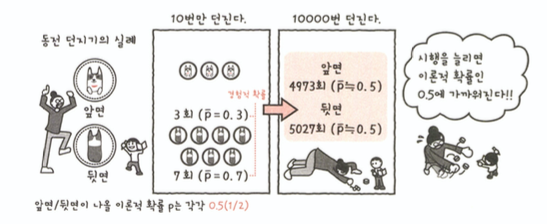
• 대수의 법칙 : 시행을 많이 반복하면 경험적 확률도 이론적 확률에 가까워진다.
  

• 표본평균에서 대수의법칙

• 표본 크기가 많아짐에 따라 참값인 모평균에 가까워진다.

• 많은 실험을 해서 데이터를 많이 관측하는 것이 측정의 정밀도를 향상시킨다는 것을 보증하고 있다.
  

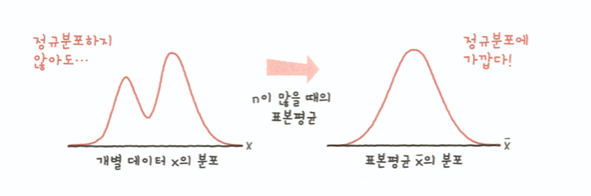
• 중심극한정리 : 개별 데이터의 모집단이 정규분포하지 않아도 추출한 표본이 충분히 크다면 표본평균은 정규분포한다는 것을 보증한다.
  

---

<연습문제> (출처: 확률 및 통계학 개론 - 13판(William Mendenhall))

(SOL)

(EOD)