Top-down Parser

• LL (Left-to-right input scan, Leftmost derivation) 문장이 있을 때, 순서대로 읽는다는 뜻 (왼쪽부터 오른쪽으로 )
  

단점

• backtrack → predictive parser
• left-recursion → 무한루프 문제

backtrack 문제

위와 같은 프로덕션 룰이 있다고 해보자

Expr → Expr + Term →Factor + Term → …
으로 바꾼다면 나중에 terminal level에서 ‘+’ 기호가 맞지 않는다는 걸 발견한다
그리고 다시 프로덕션 룰2번에서 다른 룰로 교체를 한 후에 맞는지 확인한다.

같은 프로덕션룰에서 bad pick을 한다면 backtracking해서 맞는 것으로 바꿔줘야 한다는 단점이 있다.

Left Recursion 문제

Predictive Parsing (backtrack 해결)

한단계 이후의 결과를 미리 예상하고 parsing path를 정하기 때문에 틀린 결과로 인한 backtracking을 할 필요가 없어짐 : lookahead라고 부름

다른 말로 LL Parser

left recursion

Remove left recursion

F -> Fα
	| β

F -> βF'
F' -> αF'
	| ε

Left Factoring

Predictive Parsing

FIRST()

https://m.blog.naver.com/moonsoo5522/220716279651
해당 token의 set 중에서 비교대상의 이전 terminal을 찾아주는 함수이다.

다시 말해 FIRST(A)라고 하면 A라고 하는 Set중에서 첫번째 Terminal을 찾아주는 것이다.

A->aB
A->ac
그러면 FIRST(A) = a라는 결과를 얻게 하는 것

예를 들어 다음과 같은 grammer가 있다고 생각하면

E -> TE'
E' -> +TE' 
	| ε
T -> FT'
T' -> *FT' 
	| ε
F -> (E) 
	| a

First(E)를 찾기 위해서 E -> TE' 제일 먼저 나오는 T를 찾는다.
First(T)를 찾기 위해서 T -> FT' 제일 먼저 나오는 F를 찾는다.
First(F)를 찾기 위해서 F -> (E) 와 a 를 본다.
FIRST(F) 는 {'(' , a} 이다. 따라서

	FIRST
E	(, a
E'	+, ε
T	(, a
T'	*, ε
F	(, a

FOLLOW()

https://m.blog.naver.com/moonsoo5522/220720159198
https://www.youtube.com/watch?v=WUwG50xJ9vc
비교대상 바로 다음에 나올 수 있는 terminal 들의 집합을 구해주는 함수이다.

그래서 FOLLOW(A) 라고 하면 A라는 Symbol 뒤에 나올 수 있는 Symbol들을 포함하는 것이다.

X -> YAaZ

여기서 FOLLOW(A) = {a}라고 정의할 수 있다

S -> +SS | *SS | a ;

라는 grammar가 정의되어 있다. 여기서 FOLLOW(S)를 구할 수 있을까? 그러면 각각의 derivation을 구해보면 된다. 일단 a가 나올 거라는 것은 아는 것이고, S가 가지치기를 하다보면 결국은 +도 나올 수 있고, 도 나올 수 있다.그리고 그냥 S에서 끝날경우 input string의 끝을 의미하는 $도 들어있을 것이다. 그래서 결국 FOLLOW(S) = { + , , a, $ } 라는 결과를 얻을 수 있다. 역시 Dragon Book에는 다음과 같은 수행과정을 소개하고 있다.

위의 예제를 그대로 가지고 오면

E -> TE'
E' -> +TE' 
	| ε
T -> FT'
T' -> *FT' 
	| ε
F -> (E) 
	| a

E가 시작이므로 FOLLOW(E) = {$} 에서 시작

Eα 가 있다고 했을 때 E -> TE' 룰 때문에 TE'α가 된다.
하지만 E'α 는 E로 변환될 수 있는게 없으므로 포함관계는 다음과 같다.
FOLLOW(E) ⊂ FOLLOW(E')

다음 E'에서는 ε때문에 FOLLOW(E') ⊂ FOLLOW(T) 가 성립, 이 과정에서 FOLLOW(E)에 {'+'}가 추가됨
마찬가지로 다음 룰에 따라서 FOLLOW의 포함관계를 적으면
FOLLOW(T) ⊂ FOLLOW(T')
FOLLOW(T') ⊂ FOLLOW(F), 이 과정에서 FOLLOW(T)에 {'*'}가 추가됨

그리고 마지막 룰에서 FOLLOW(E) = {$ , ')'} 가 됨

포함관계를 따져보면
FOLLOW(E) ⊂ FOLLOW(E') ⊂ FOLLOW(T) ⊂ FOLLOW(T') ⊂ FOLLOW(F)
인데 FOLLOW(E) = {$ , ')'} 이고 FOLLOW(E)에 {'+'}가 추가됨, FOLLOW(T)에 {'*'}가 추가됨 이므로 다음과 같다.

	FIRST	FOLLOW
E	(, a	$, )
E'	+, ε	$, )
T	(, a	$, ), +
T'	*, ε	$, ), +
F	(, a	$, ), +, *

The LL(1) Property

First(α)◠First(β) = ϕ
First+(α) 는 First(α)◡Follow(α) 를 의미
Then, a grammar is LL(1) iff A -> α and A -> β implies
First+(α)◠First+(β) = ϕ

---

예제)

FIRST(e) = { ‘(’ , ‘x’ , ‘y‘ }
FOLLOW(e) = { $ , ‘)’ }

Table template을 만들어야 하는데 이때 Row 쪽에는 nonterminal / Coloum쪽에는 terminal로 배치

그 후 Production에 대한 first를 찾아서 하나씩 삽입

ε이 나왔을 때 : e' -> ε 인데 FIRST( ε ) 이라는 의미는 없으므로 이 때는 FOLLOW(e')를 찾아서 집어넣어주면 된다

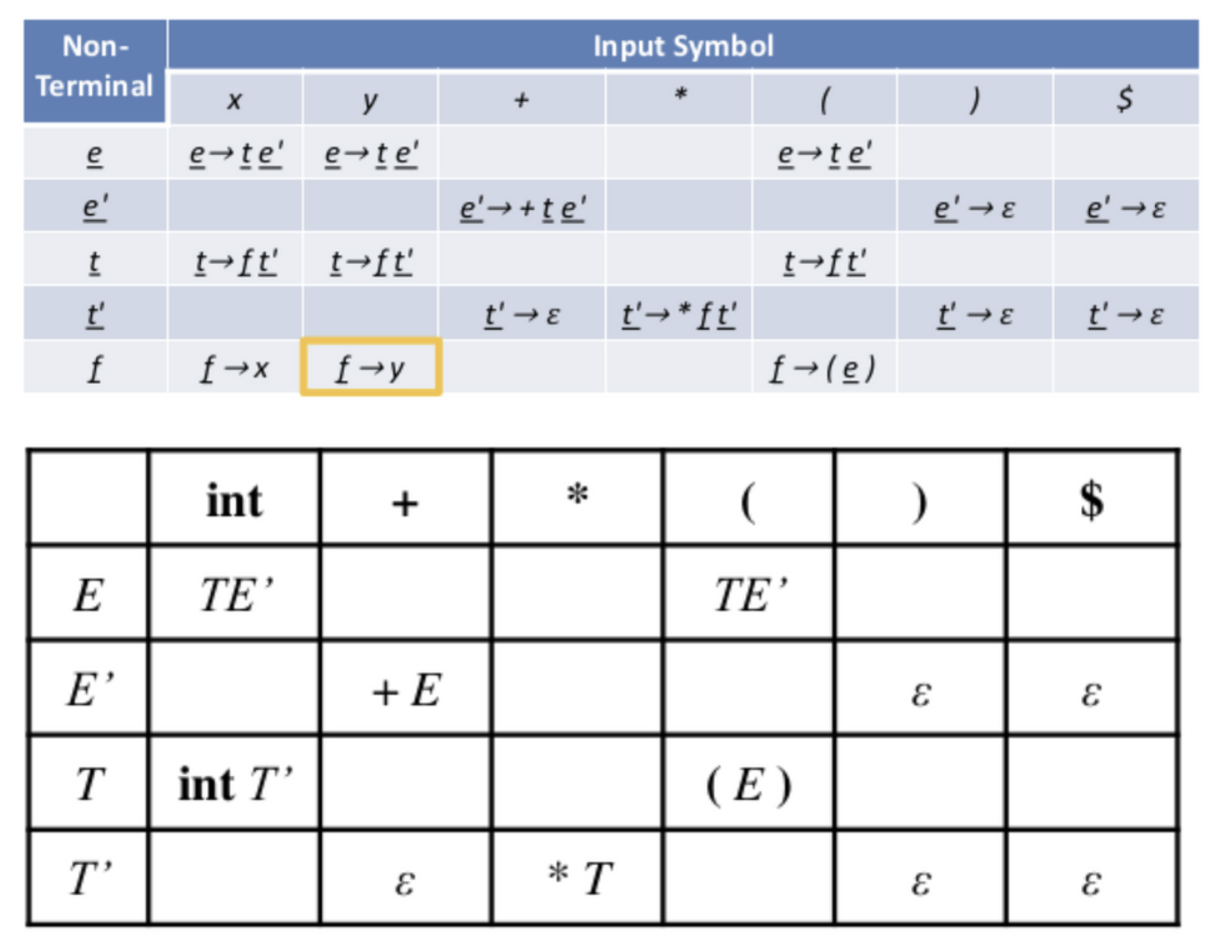
예제2

First Follow table 만든 후 -> First를 따라서 table을 완성함, ε가 나온다면 Follow를 따라감