동적 계획법
주어진 큰 문제를 중복되지 않은 작은 문제로 분할하여 해결하는 알고리즘
큰 문제를 작은 문제로 분할하여 해결하는 분할 정복(Divide and Conquer)과 비슷한데 가장 큰 차이점이 분할 정복은 작은 문제의 중복이 있을 수 있고 동적 계획법은 중복이 일어나지 않도록 하는 것이다.
중복되는 문제
피보나치 수열을 예시로 살펴보자.
피보나치 수열은 첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열이다.
따라서 F(n) = F(n-1) + F(n-2)이 된다.
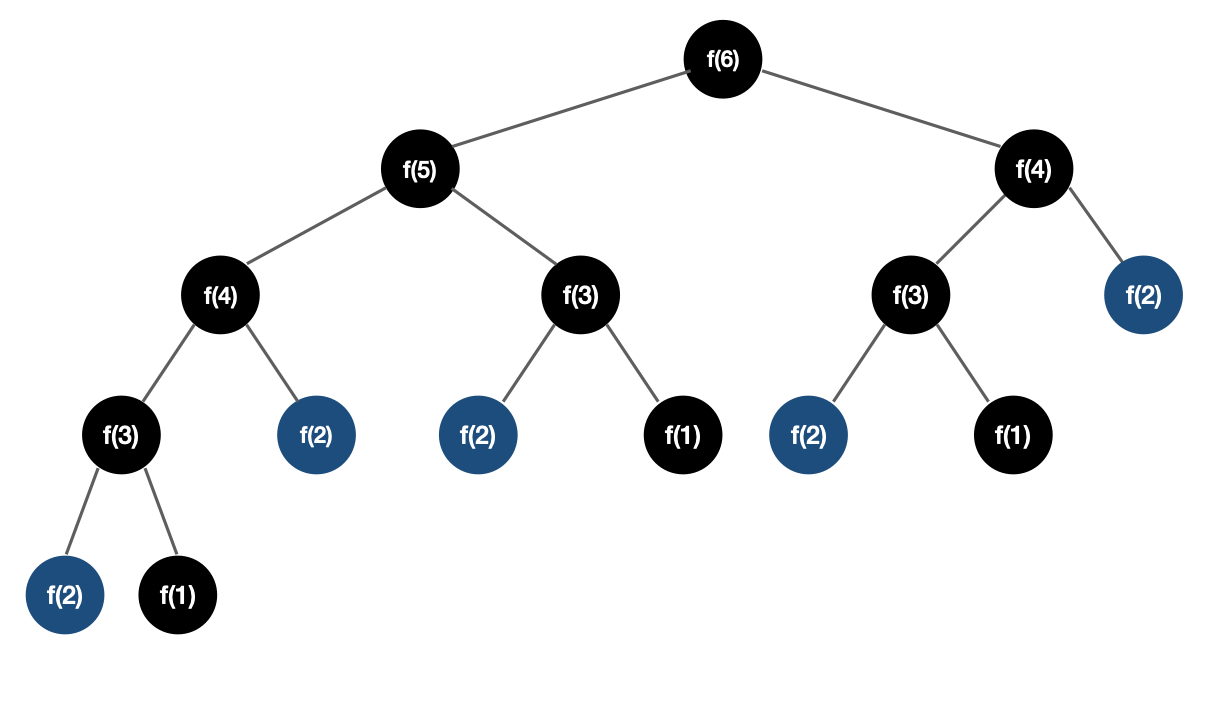
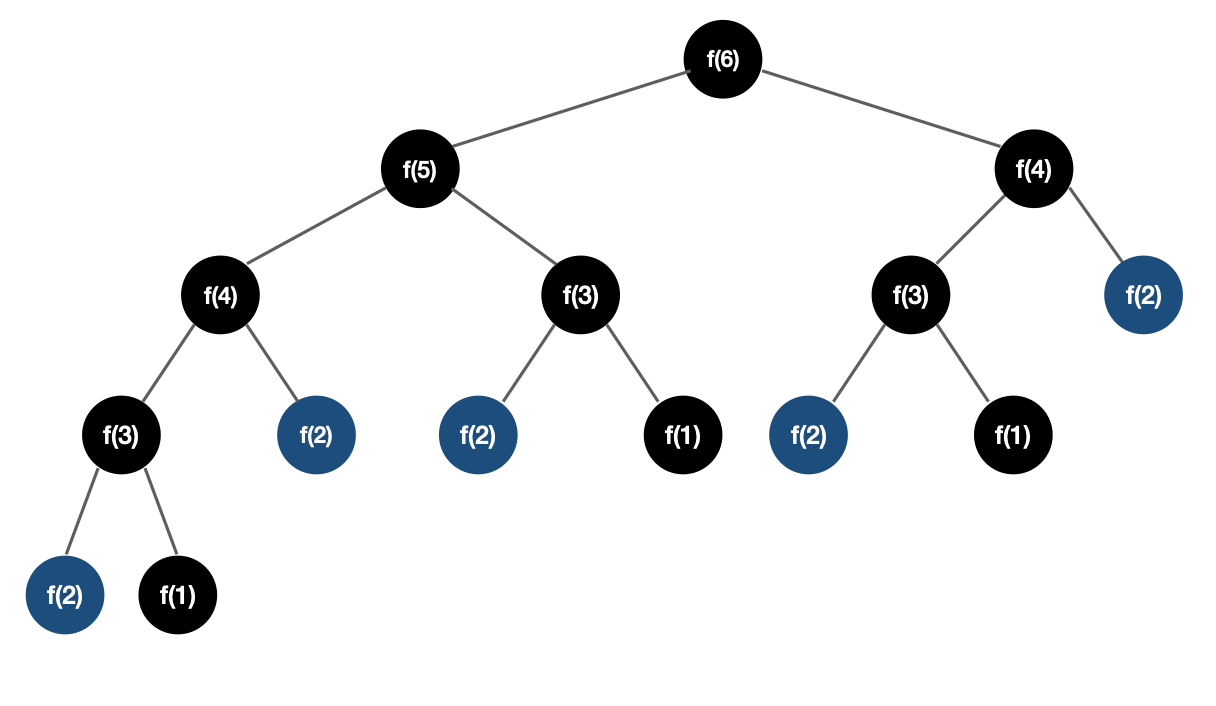
그림에서 볼 수 있듯이 F(6)을 구하려면 큰 문제를 여러 개의 작은 문제들로 분할해서 구할 수 있는데 그 과정에서 F(2)가 5번이나 반복되는 것을 볼 수 있다.
이러한 중복되는 문제를 해결하기 위해서 나온 것이 동적 계획법이다.
동적 계획법의 조건
동적 계획법의 조건은 2가지가 있다.
- 최적 부분 구조(Optimal Substructure)
- 중복 되는 부분 문제(Overlapping Subproblem)
최적 부분 구조는 큰 문제를 작은 문제로 나누어 해결할 수 있다는 것이다.
ex) 피보나치 수열 F(n) = F(n-1) + F(n-2)
중복되는 부분 문제는 작은 문제로 나눌 때 작은 문제들에 중복이 있다는 것이다.
피보나치 수열에서 보았던 F(2)가 반복되는 것이 여기에 해당한다.
중복되는 작은 문제들은 항상 답이 똑같기 때문에 매번 계산하게 된다면 많은 시간이 소모된다. 이러한 중복 계산을 방지하기 위해 동적 계획법을 사용하며, 분할 정복보다 시간을 많이 절약할 수 있다.
동적 계획법의 종류
동적 계획법은 2가지 방식이 있는데 방식에 따라 사용되는 기법이 다르다.
Top-Down 방식(하향식)
Top-Down 방식은 상위 문제부터 하위 문제로 해결하는 방식으로 하향식이라고도 부른다.
이 방식은 재귀 호출을 사용하여 문제를 해결하는데, 이 과정에서 Memoization을 사용한다.
Memoization: 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술
java 코드로 살펴보자.
import java.util.HashMap;
import java.util.Map;
public class Fibonacci {
public static int fibonacci(int n, Map<Integer, Integer> cache) {
if (cache.containsKey(n)) {
return cache.get(n);
}
int result;
if (n == 0) {
result = 0;
} else if (n == 1) {
result = 1;
} else {
result = fibonacci(n - 1, cache) + fibonacci(n - 2, cache);
}
cache.put(n, result);
return result;
}
public static void main(String[] args) {
int n = 6; // Find the 6th Fibonacci number
Map<Integer, Integer> cache = new HashMap<>();
int result = fibonacci(n, cache);
System.out.println("The " + n + "th Fibonacci number is: " + result);
}
}
cache를 선언해서 fibonacci 함수내에서 값을 저장하고 if 조건문에 의해 중복된 문제인 경우 계산하지 않고 넘어간다.
이러한 방식이 Memoization이다.
Bottom-Up 방식(상향식)
Bottom-Up 방식은 하위 문제로부터 상위 문제로 해결하는 방식으로 상향식이라고도 부른다.
Top-Down에서 Memoization을 사용했다면 Bottom-Up에선 Tabulation을 사용한다.

Tabulation은 표를 하나씩 채워 올라가는 것으로 반복문을 사용하여 해결할 수 있다.
java 코드로 살펴보자.
import java.util.Arrays;
public class Fibonacci {
public static int fibonacci(int n) {
if (n == 0) {
return 0;
} else if (n == 1) {
return 1;
} else {
int[] table = new int[n + 1];
table[0] = 0;
table[1] = 1;
for (int i = 2; i <= n; i++) {
table[i] = table[i - 1] + table[i - 2];
}
return table[n];
}
}
public static void main(String[] args) {
int n = 6; // Find the 6th Fibonacci number
int result = fibonacci(n);
System.out.println("The " + n + "th Fibonacci number is: " + result);
}
}
fibonacci 함수 내에서 int형 배열 table을 선언해서 for 반복문으로 테이블에 순서대로 값을 저장하면서 해결하는 것을 볼 수 있다.
2가지 방법 모두 동적 계획법이며 접근 방식 외엔 다른 점이 없어 상황에 따라 2가지 방법 중 하나를 골라서 사용하면 된다.
요약
- 동적 계획법은 큰 문제를 중복되지 않은 작은 문제로 나누어 해결하는 알고리즘이다.
- 분할 정복에서 반복되는 중복 문제를 해결할 수 있어 시간을 절약할 수 있다.
- 종류로는 Top-Down 방식, Bottom-Up 방식 2가지가 있으며 접근 방식에 따라 사용하는 기법이 Memoization, Tabulation으로 나뉜다.