DFS & BFS?

DFS - 깊이 우선 탐색

1. 루트 노드를 스택에 넣고 방문처리 한다.
2. 스택 최상단 노드의 인접 노드 중 방문하지 않은 노드 하나를 스택에 넣고 방문처리한다.
3. 2단계를 더 이상 수행할 수 없을 때 까지 (스택이 빌 때 까지) 반복한다.

BFS - 너비 우선 탐색

1. A노드를 방문하고, 인접 노드인 B, C를 큐에 넣는다.
2. 큐에서 B를 꺼내고, B의 인접 노드인 D, E를 큐에 넣는다.
3. 큐에서 C를 꺼내고, C의 인접 노드인 F를 넣는다.
4. 큐에서 D를 꺼낸다. 인접 노드이면서 아직 방문되지 않은 노드가 없으므로 큐에 넣을 건 없다.
5. 큐에서 E를 꺼낸다. 마찬가지로 큐에 넣을 노드는 없다.
6. 큐에서 F를 꺼내고 모든 노드를 탐색했으므로, 탐색을 종료한다.

그래프 - 1260, 11724, 1707, 10451, 2331, 9466, 2667, 4963, 7576, 2178, 2146, 1991, 11725, 1167, 1967
출처: https://plzrun.tistory.com/entry/알고리즘-문제풀이PS-시작하기 [plzrun's algorithm:티스토리]

1260

#include <iostream>
#include <queue>
#include <vector>
using namespace std;

#define MAX 1001

int n, m, v, from, to;
int map[MAX][MAX]; //인접 행렬 그래프
bool visited[MAX]; //정점 방문 여부
queue<int> q;
vector<int> e[1001];

void reset() {
    for (int i = 1; i <= n; i++) {
        visited[i] = 0;
    }
}

void DFS(int v)
{
    visited[v] = 1;
    cout << v << " ";

    for (int i = 1; i <= n; i++){
        if (map[v][i] == 1 && visited[i] == 0) // 인접정점 중 방문하지 않은 것.
            DFS(i);
    }
}

void BFS(int v)
{
    q.push(v);
    visited[v] = true;
    cout << v << " ";
 
    while (!q.empty()) {
        v = q.front();
        q.pop();
        
        for (int w = 1; w <= n; w++) {
            if (map[v][w] == 1 && visited[w] == 0) { //현재 정점과 인접노드이고 방문되지 않았으면
                q.push(w);
                visited[w] = true;
                cout << w << " ";
            }
        }
    }
}

int main()
{
    cin >> n >> m >> v;
    for (int i = 0; i < m; i++) {
		cin >> from >> to;
		map[from][to] = 1;
        map[to][from] = 1;
	}
 
    reset();
    DFS(v);
    
    cout << '\n';
    
    reset();
    BFS(v);
  
	return 0;
}

11724

#include <vector>
#include <iostream>
using namespace std;

#define MAX 1001

int N, M;
int map[MAX][MAX];
bool visited[MAX]; //정점 방문 여부

void DFS(int v)
{
    visited[v] = 1;

    for (int i = 1; i <= N; i++){
        if (map[v][i] == 1 && visited[i] == 0) // 인접정점 중 방문하지 않은 것.
            DFS(i);
    }
}

int Components(int count){
    fill(visited, visited + N, false);

    for (int i = 1; i <= N; i++)
    {
        if (!visited[i])
        {
            DFS(i); // 실행 시 연결된 노드는 visited = 1이 된다.
            count++;
        }
    }
    return count;
}

int main(){

    int from, to;
    cin >> N >> M;

    for (int i = 1; i <= M; i++)
    {
        cin >> from >> to;
        map[from][to] = 1;
        map[to][from] = 1;
    }

    cout << Components(0);
}

연결된 구성요소들을 알아보는 함수를 만들어 총 몇개의 묶음으로 되어있는지 알아보는 함수이다.

1707

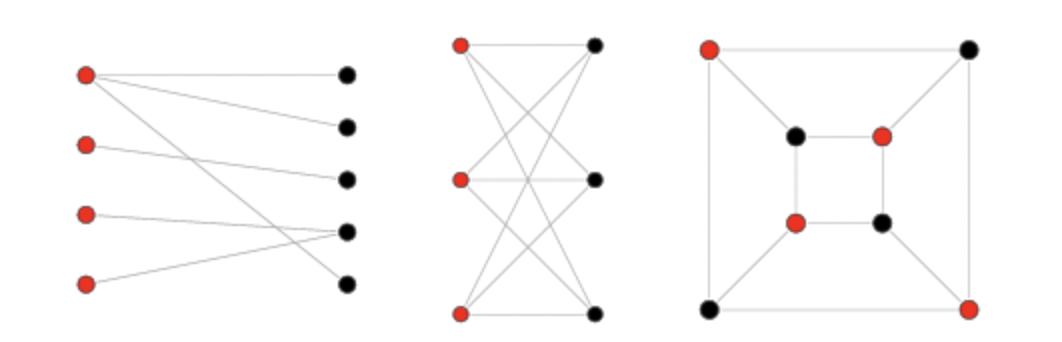
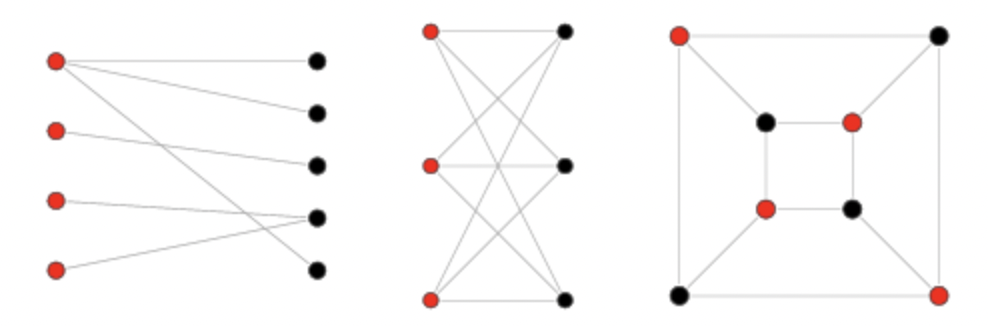
이분 그래프

이분 그래프(Bipartite Graph)란

인접한 정점끼리 서로 다른 색으로 칠해서 모든 정점을 두 가지 색으로만 칠할 수 있는 그래프

• 이분 그래프인지 확인하는 방법은 BFS, DFS 탐색을 이용하면 된다.
• 이분 그래프는 BFS를 할 때 같은 레벨의 정점끼리는 모조건 같은 색으로 칠해진다.
• 연결 성분의 개수(Connected Component)를 구하는 방법과 유사하다.
• 모든 정점을 방문하며 간선을 검사하기 때문에 시간 복잡도는 O(V+E)로 그래프 탐색 알고리즘과 같다.

#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;

#define MAX_SIZE 20001
#define RED  1
#define BLUE 2

int K, V, E; // 테스트 케이스, 노드, 링크 선언
vector<int> graph[MAX_SIZE];
int visited[MAX_SIZE];

void bfs(int start);
bool isBipartiteGraph();

void bfs(int start)
{
    queue<int> q;
    int color = RED;

    visited[start] = color;
    q.push(start);
    while (!q.empty())
    {
        int now = q.front();
        q.pop();

        if (visited[now] == RED) // 현재 노드의 색
            color = BLUE; // 반대로 바꾸기
        else if (visited[now] == BLUE)
            color = RED;
        
        int gsize = graph[now].size();
        for (int i = 0; i < gsize; i++){
            // 현재 노드의 인접 노드를 칠하기
            int next = graph[now][i];
            if (!visited[next]) // 인접 노드가 칠해져 있지 않다면
            {
                visited[next] = color;
                q.push(next);
            }
        }
    }
}

bool isBipartiteGraph()
{
    for (int i = 1; i <= V; i++)
    {
        int gsize = graph[i].size();
        for (int j = 0; j < gsize; j++)
        {
            int next = graph[i][j];
            if (visited[i] == visited[next]) // 현재 노드 색== 인접 노드 색
                return 0; // return false 
        }
    }
    return 1;
}

int main(){

    int from, to;
    cin >> K;
    while (K--)
    {
        cin >> V >> E;
        for (int i = 0; i < E; i++)
        {
            cin >> from >> to;
            graph[from].push_back(to);
            graph[to].push_back(from);
        }

        for (int i = 1; i <= V; i++)
        {
            if (!visited[i])
                bfs(i);
        }

        if (isBipartiteGraph())
            cout << "YES\n";
        else
            cout << "NO\n";

        for (int i = 1; i <= V; i++) {
            graph[i].clear();
        }
        memset(visited, false, sizeof(visited));
    }
}