DP(dynamic programming)

dynamic programming은 하나의 문제는 단 한번만 풀도록 하는 알고리즘이다.

출처 : https://blog.naver.com/ndb796/221233570962
피보나치 수열을 통해 더욱 쉽게 이해할 수 있다.

int f(int x)
{
	if (x == 1) return 1;
	if (x == 2) return 1;
	return d(x - 1) + d(x - 2);
}

int f(int x)
{
	if (x == 1) return 1;
	if (x == 2) return 1;
    if (d[x] != 0) return d[x];
	return (d[x] = d(x - 1) + d(x - 2));
}

이 두 코드를 비교해보자
위의 코드의 경우에는 f(12)를 계산하고 나서도 f(13)을 위해서는 다시 f(12)를 위한 재귀를 반복해야한다.
하지만 아래의 코드는 값을 배열에 저장해주기 때문에 f(12)를 구하기 위해 다시 재귀할 필요가 없다.

boj dp 문제
DP - 1463, 11726, 11727, 9095, 10844, 11057, 2193, 9465, 2156, 11053, 11055, 11722, 11054, 1912, 2579, 1699, 2133, 9461, 2225, 2011, 11052
출처: https://plzrun.tistory.com/entry/알고리즘-문제풀이PS-시작하기 [plzrun's algorithm:티스토리]

---

1463

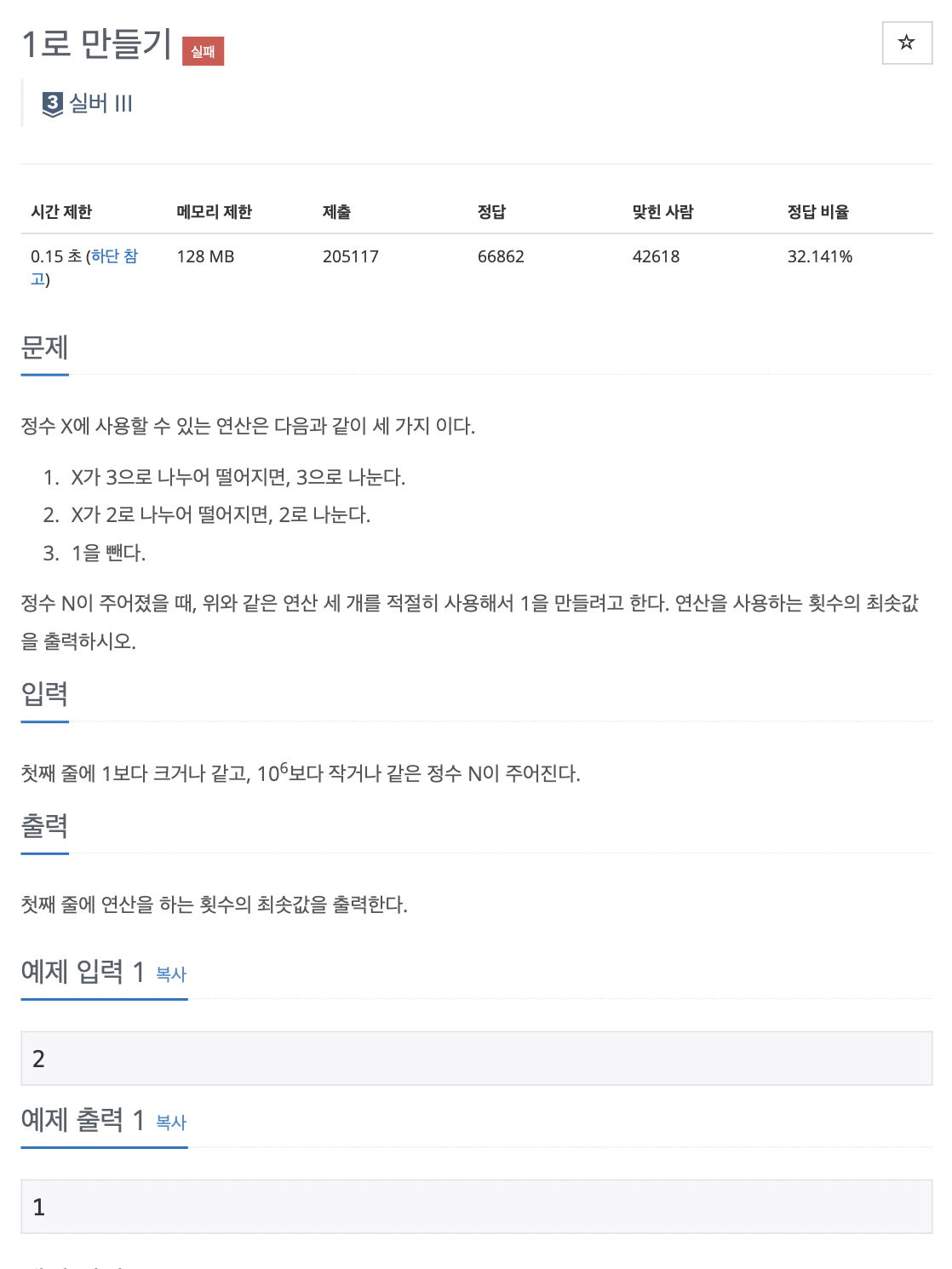
dp[n]을 숫자 N을 1로 만들 수 있는 최소 가짓 수라고 할 때
문제 조건을 이용해서 만들 수 있는 방법의 수는

1. dp[n - 1] + 1 ex) 5의 결과를 찾는 법 -> 4의 결과 + 1
2. dp[n / 2] + 1 ex) 8의 결과를 찾는 법 -> 8/2 = 4의 결과 + 1
3. dp[n / 3] + 1 ex) 9의 결과를 찾는 법 -> 9/3 = 3의 결과 + 1

dp이므로 각 값의 결과를 배열에 저장시켜주면서 다시 연산할 필요 없도록 한다.

#include <iostream>
#include <vector>
using namespace std;

int main(){
    int N;
    
    cin >> N;
    vector<int> dp(N + 1);

    dp[0] = 0;
    dp[1] = 0;
    dp[2] = 1;
    dp[3] = 1;

    for (int i = 4; i <= N; i++)
    {
        dp[i] = dp[i - 1] + 1; // 방법 1
        if (i % 2 == 0) dp[i] = min(dp[i], dp[i / 2] + 1); // 방법 1과 방법 2를 비교하여 둘 중 작은 걸 선택
        if (i % 3 == 0) dp[i] = min(dp[i], dp[i / 3] + 1); // 방법 1과 방법 2를 비교하여 둘 중 작은 걸 선택
    }

    cout << dp[N];
}

11726

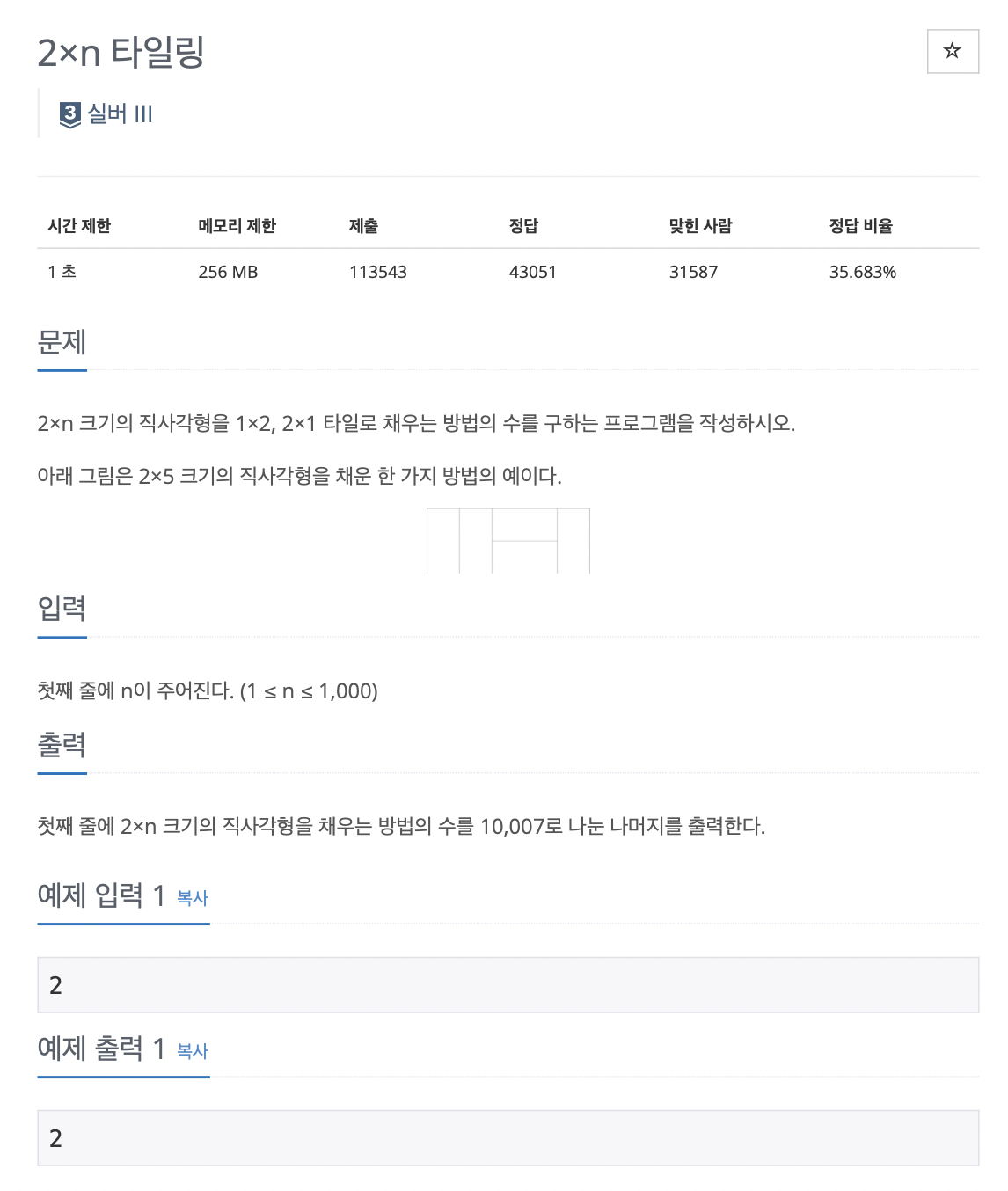
n번째 방법의 수를 구하는 방법은 d(x - 1) + d(x - 2)를 하면 된다.

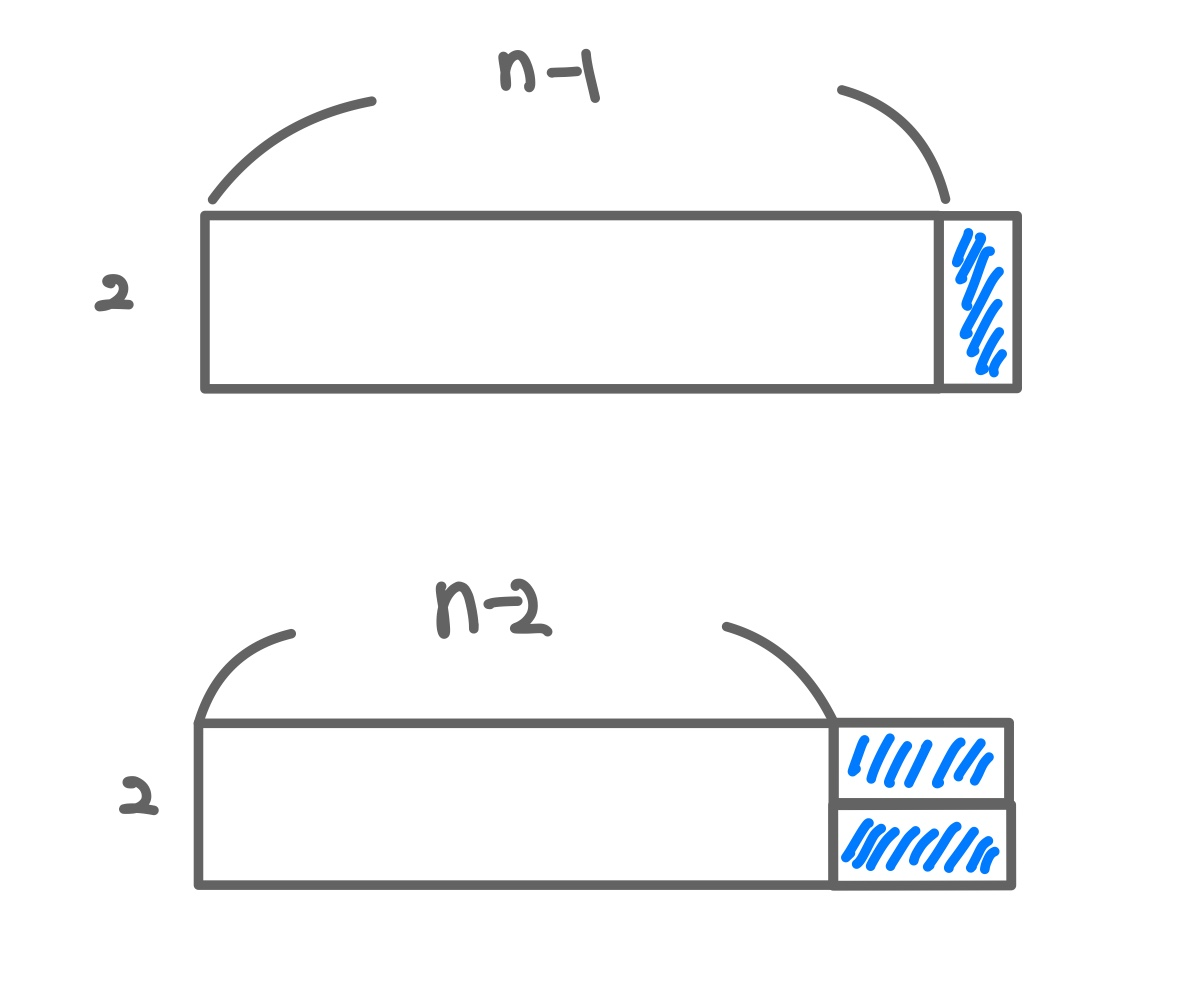
d(x-1)에서 마지막에 타일하나를 붙인 경우의 수와 d(x-2)에서 마지막에 가로타일 2개를 붙인 경우를 더하기만 하면 되기 때문이다.

#include <vector>
#include <iostream>
using namespace std;

int main(){
    int n;

    cin >> n;
    vector<int> dp(n+1);

    // n은 자연수이기 때문에 1부터 시작하도록 한다.
    dp[1] = 1;
    dp[2] = 2;

    for (int i = 3; i <= n; i++)
    {
        dp[i] = (dp[i - 1] + dp[i - 2]) % 10007;
    }

    cout << dp[n];
}

11727

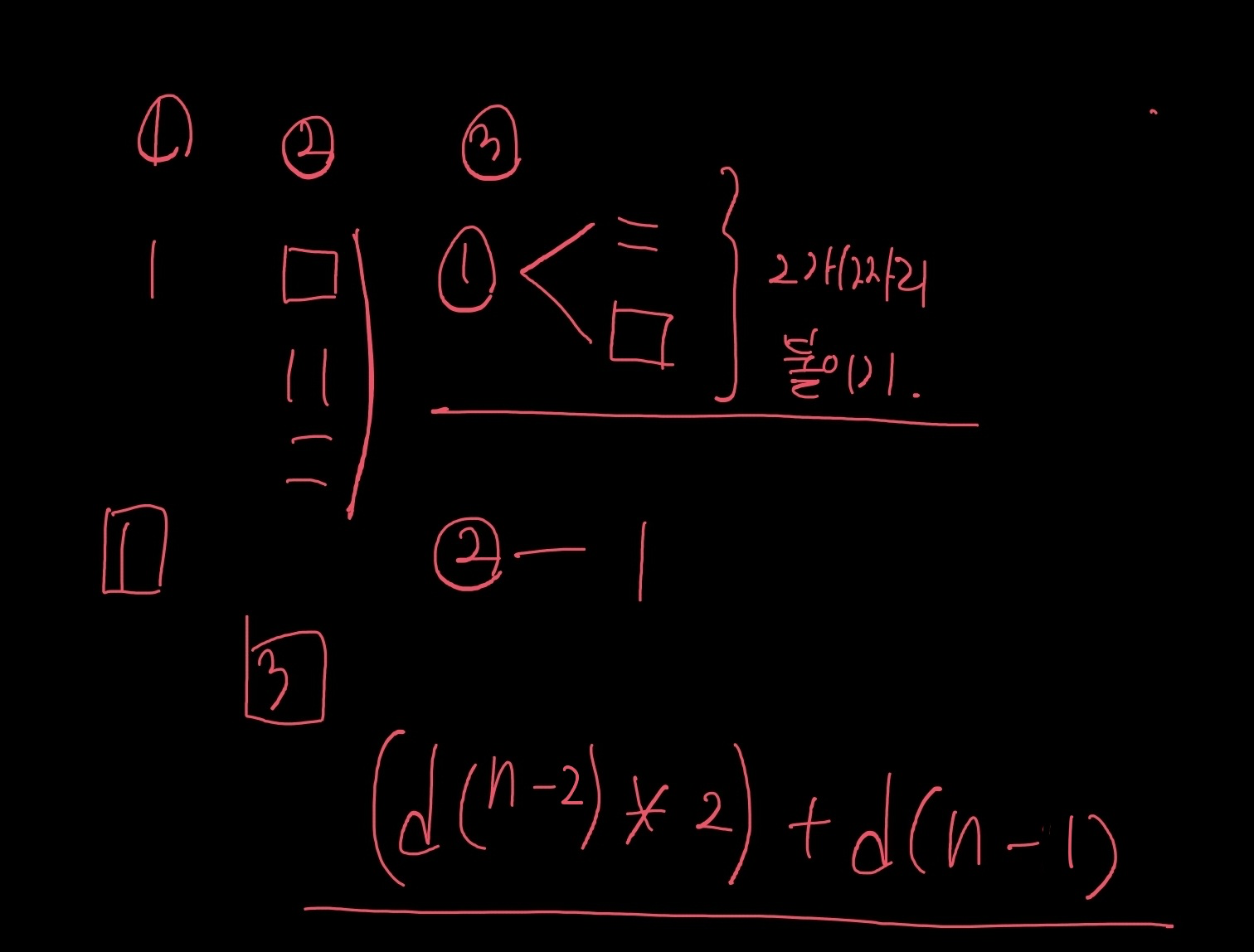
#include <vector>
#include <iostream>
using namespace std;

int main(){
    int n;

    cin >> n;
    vector<int> dp(n+1);

    // n은 자연수이기 때문에 1부터 시작하도록 한다.
    dp[1] = 1;
    dp[2] = 3;

    for (int i = 3; i <= n; i++)
    {
        dp[i] = ((2 * dp[i - 2]) + dp[i - 1]) % 10007;
    }

    cout << dp[n];
}