알고리즘(2부: DFS, BFS)

이번 포스팅에서는 1부 서론에 이어서 그래프 탐색 알고리즘인 DFS(Depth First Search, 깊이 우선 탐색), BFS(Breadth Frist Search, 너비 우선 탐색)에 대해 알아보자

먼저 그래프에 대해서 간단히 정의하자면 아래와 같다.

• 정점과 정점(node)들을 연결하는 간선으로 이루어진 자료구조의 일종

그래프를 탐색한다라는 것의 의미는 그래프 상의 모든 정점을 하나의 정점에서부터 차례대로 방문한다는 의미다.

말로만 들어서는 잘 와닿지 않기에 아래 그림을 참고하면서 보자

출처

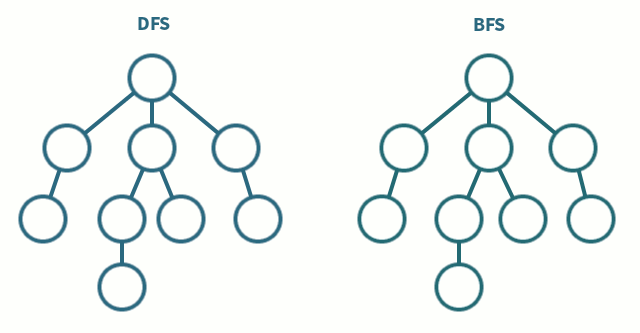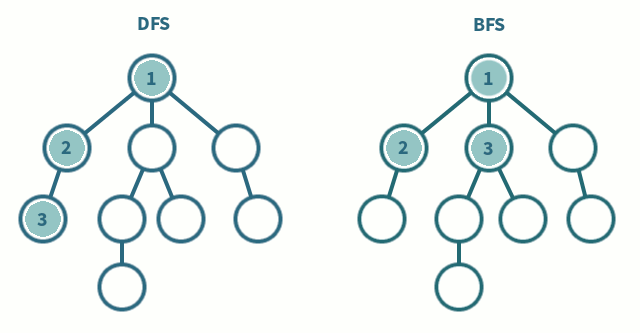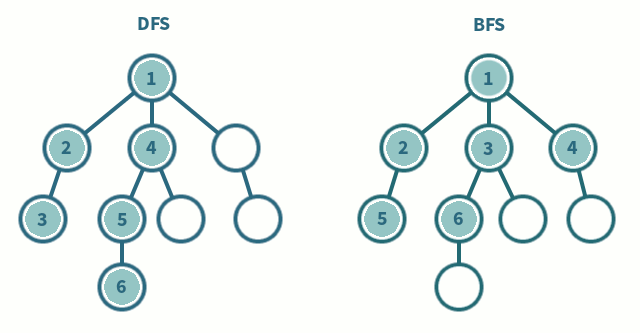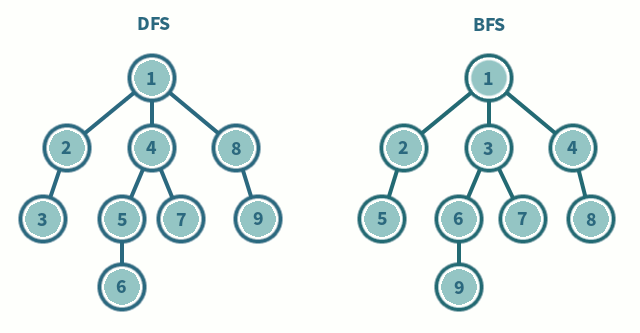
위 그림에서 동그라미들이 정점이고 그 동그라미들을 이어주는 선이 간선이다.
또한, DFS와 BFS의 가장 큰 차이점은 정점 방문 순서가 다르다는 것을 한 눈에 알아 볼 수가 있다.
지금부터 DFS와 BFS에 대해 좀 더 자세히 알아보자

---

DFS(Depth First Search, 깊이 우선 탐색)

깊이 우선 탐색이라는 말과 같이 루트 노드에서 시작하여 한쪽 분기를 먼저 깊게 탐색하고 끝에 도달했을 때 다음 분기로 옮겨가 깊이 탐색을 실시하는 방식이다.

동작 방식

• 시작 정점을 스택에 삽입하고 방문 처리
• 스택의 최상단 정점에 방문하지 않은 인접 정점을 스택에 넣고 방문 처리
• 위 과정을 수행할 수 없을 때까지 반복

특징

• 스택이나 재귀함수로 구현이 가능
• BFS에 비해 간단한 구현
• 현재 분기만 기억하면 되기에 메모리 공간 차지가 적음
• 목표 정점이 깊은 단계에 있을 경우 빠른 결과 도출 가능
• 답이 아닌 분기 탐색 시, 해당 분기에 깊이 빠지게 되어 시간 낭비
• 무한한 길이를 가진 분기 탐색 시, 해당 분기에서 빠져나오지 못함 (해당 분기에 답이 없다면)
• 최단 거리를 구해야하지만 목표로 갈 수 있는 길이 다수인 경우, 구한 거리가 최단 거리가 아닐 수도 있음

---

BFS(Breadth Frist Search, 너비 우선 탐색)

너비 우선 탐색이라는 말과 같이 루트 노드에서 시작하여 인접 정점들을 모두 탐색하고 다음 인접 정점들을 계속해서 탐색해 나가는 너비 탐색을 실시하는 방식이다.

동작 방식

• 시작 정점을 큐에 삽입하고 방문 처리
• 큐에서 정점을 꺼내고 해당 정점의 방문하지 않은 모든 인접 정점을 큐에 넣고 방문 처리
• 위 과정을 수행할 수 없을 때까지 반복

특징

• 큐로 구현이 가능
• 모든 경로를 탐색하므로, 최단 거리 탐색에 유용
• 무한한 길이를 가진 분기가 있어도, 모든 분기를 탐색하며 가기에 답 도출 가능
• 정점/분기가 많아질수록 메모리 공간 차지가 많아짐(공간 복잡도가 커짐)

---

백준 1260(DFS와 BFS) 문제

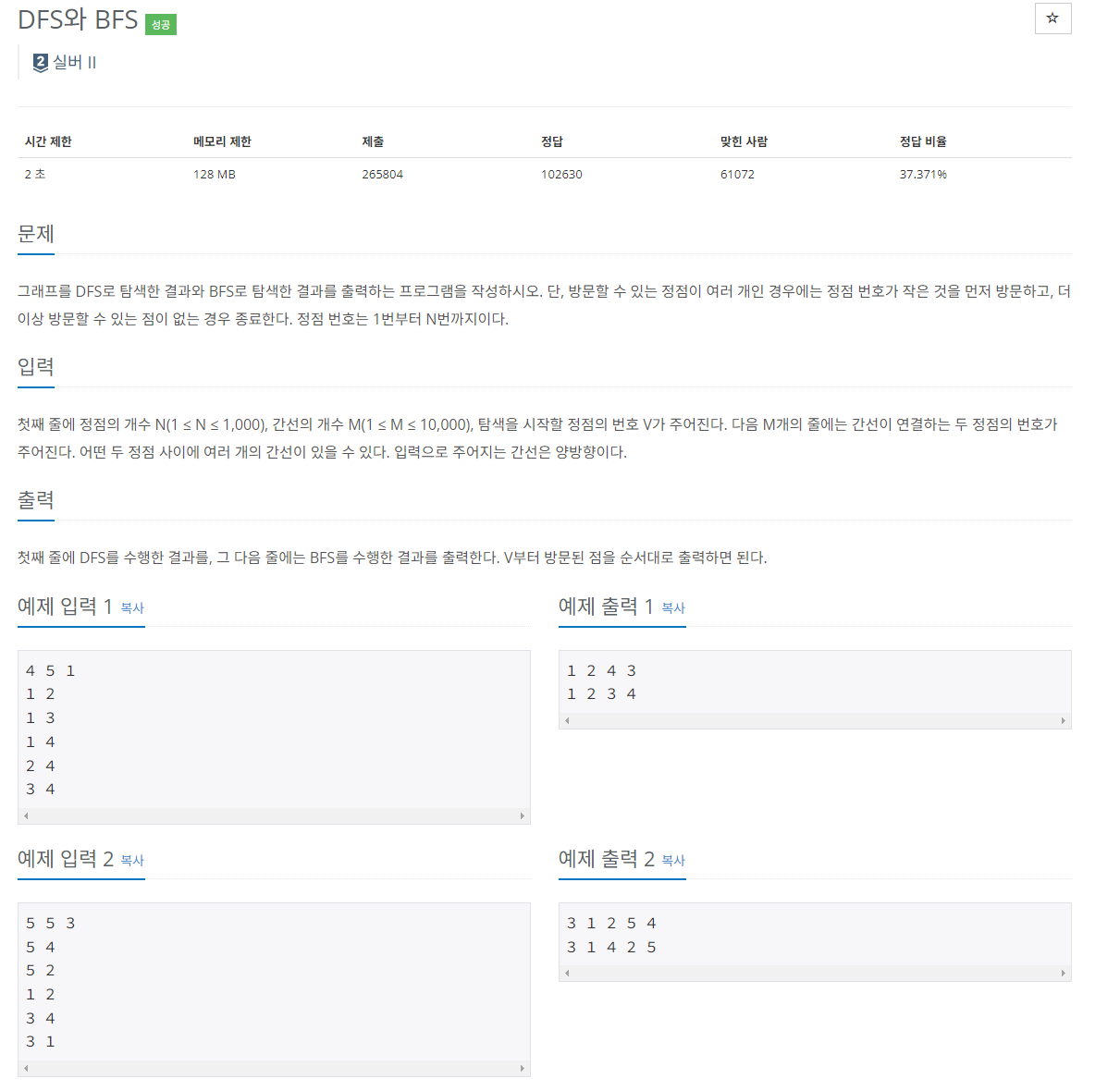
간단하게 DFS와 BFS를 구현해 볼 수 있는 문제로 문제 풀이는 아래와 같음

import sys
from collections import deque

input = sys.stdin.readline
# 재귀 깊이 제한 설정
sys.setrecursionlimit(10 ** 6)

n, m, v = map(int, input().split())

graph = [[] for _ in range(n+1)]

# 그래프 그리기
for _ in range(m):
  a, b = map(int, input().split())
  graph[a].append(b)
  graph[b].append(a)

# 정점 번호 정렬
for i in range(n+1):
  graph[i].sort()

def dfs(v):
  # 정점 방문 처리
  visited[v] = 1
  print(v, end = ' ')

  for i in graph[v]:
    if not visited[i]:
      dfs(i)

def bfs(v):
  q = deque([v])
  #정점 방문 처리
  visited[v] = 1

  while q:
    v = q.popleft()
    print(v, end = ' ')

    for i in graph[v]:
      if not visited[i]:
        q.append(i)
        visited[i] = 1


visited = [0] * (n+1)
dfs(v)

print()
visited = [0] * (n+1)
bfs(v)