병합정렬 알고리즘(merge sort algorithm)

1. Merge Sort Algorithm

---

병합정렬 알고리즘은 천재만재 폰 노이만 선생님께서 1948년에 최초로 작성하신 알고리즘이다.

당시 EDVAC이라는 컴퓨터에서 6천개 가량의 진공관을 통해 작성되는 23페이지의 코드였다고 한다. (ㄷㄷ)

병합정렬 알고리즘은 크게 분할, 병합, 정렬이라는 세가지 컨셉으로 이루어져 있는데, 0개 또는 1개의 요소를 가진 배열은 이미 정렬되어있다는 점을 활용한 알고리즘이다.

빈 배열[]이나 배열[1]은 이미 정렬 되어 있다.

따라서 주어진 원 배열을 0 또는 1개의 요소를 가진 배열이 될 때까지(base case) 계속해서 반으로 쪼갠 뒤 새로운 배열을 만들어낸다.

[5,3,2,4,1] 배열을 [5],[3],[2],[4],[1]로 나눈다.

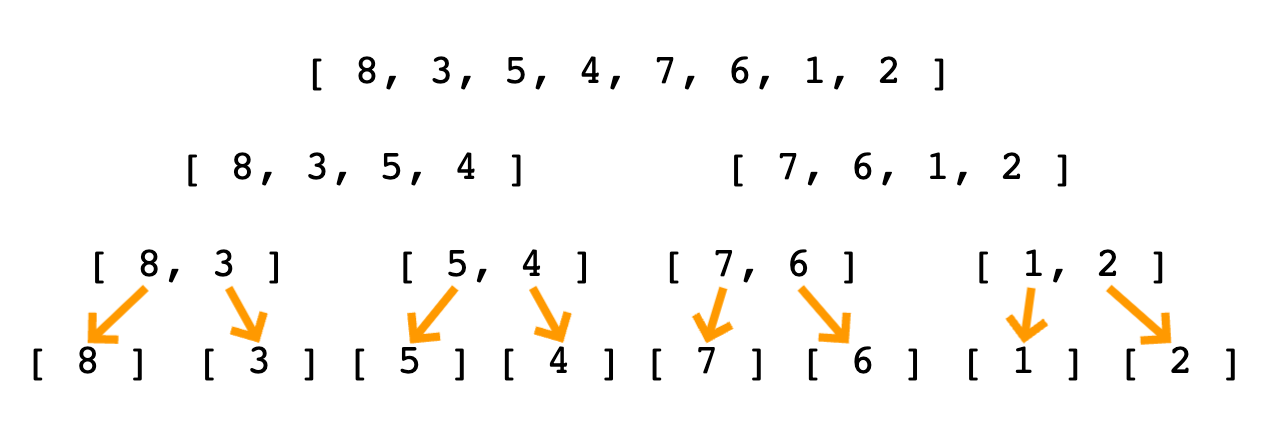
배열이 모두 분할되었다면 이제 두 개의 배열씩 비교, 정렬하여 병합된 배열을 만들어낸다.

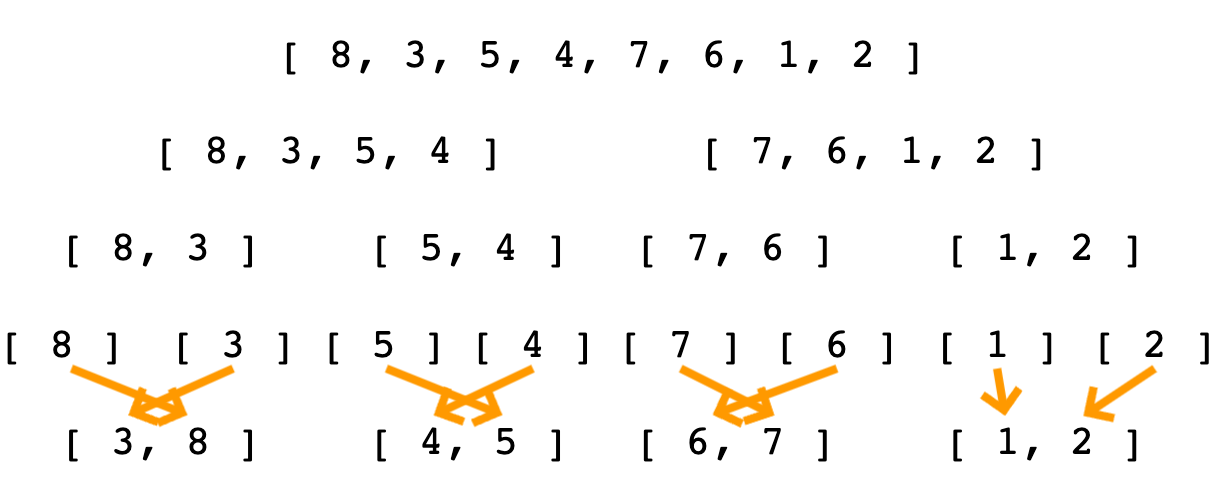
각 배열의 요소가 두 개 이상인 경우(이미 정렬되어 있음) 두 배열의 첫 번째 요소들 부터 비교해가며 다시 하나의 배열로 합친다.

이런 식으로 전체 배열이 하나가 될 때까지 합치는 과정을 거치면 정렬된 배열을 얻을 수 있다.

좀더 시각적으로 확인해보자.

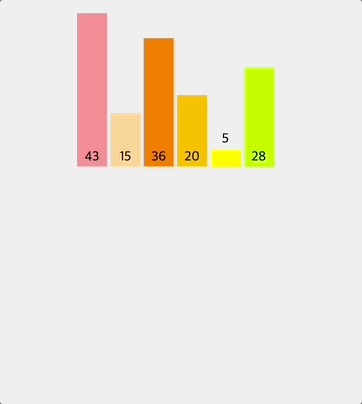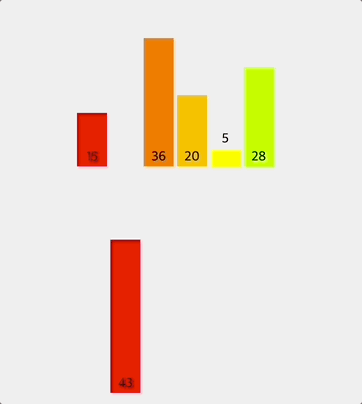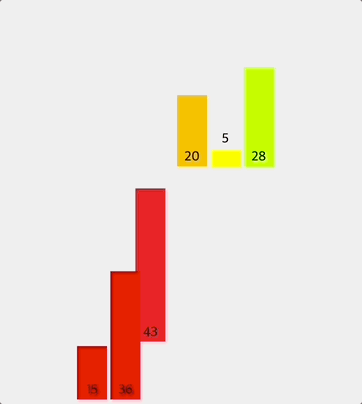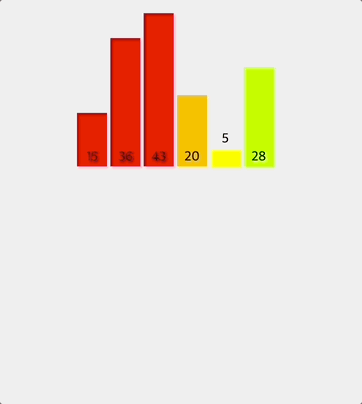
전체 배열을 반으로 나누어서 먼저 왼쪽 반을 두 요소씩 비교하여 정렬한다.

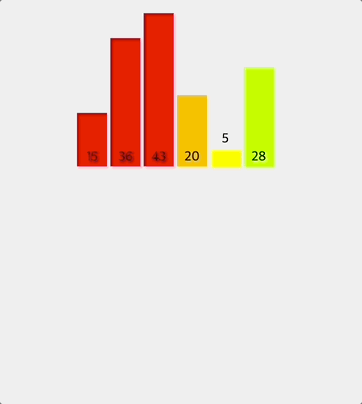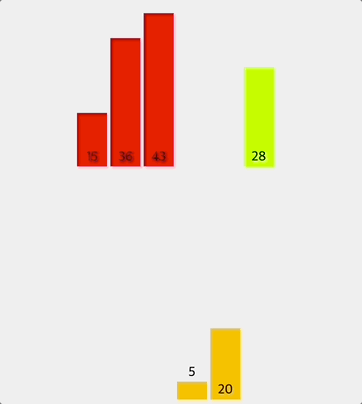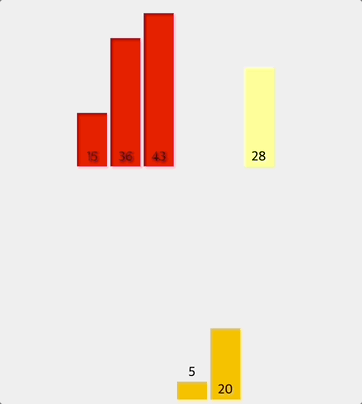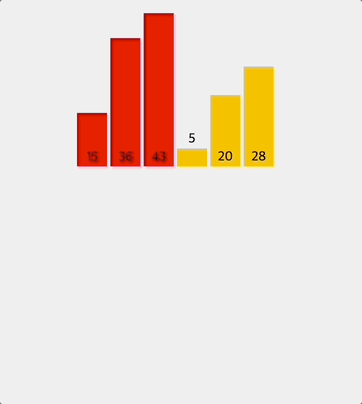
나머지 반쪽도 똑같은 방식으로 정렬한다.

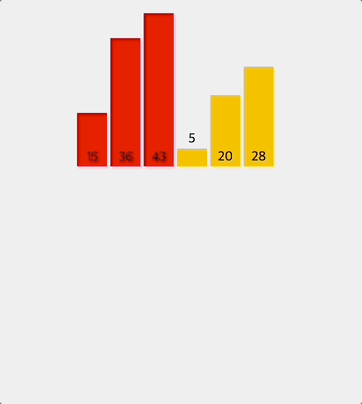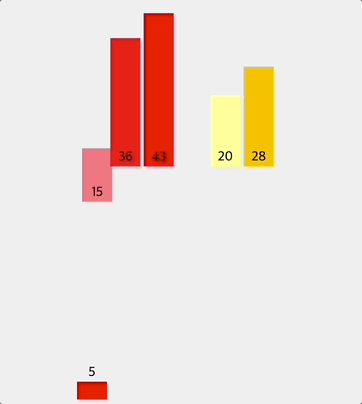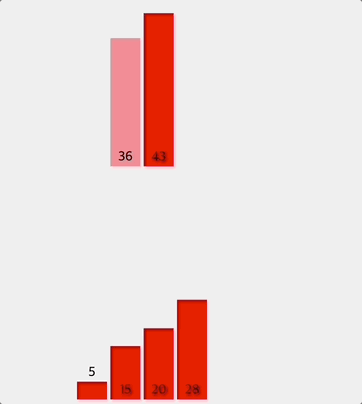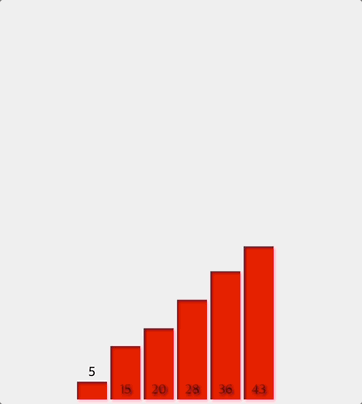
정렬된 왼쪽과 오른쪽을 최종적으로 병합한다.

2. application example

---

병합정렬을 하기 위해서는 두 개의 함수가 필요하다.

1. 두 개의 배열을 하나의 정렬된 새 배열로 만드는 함수 merge
2. 원 배열을 반으로 나누고 최종적으로 다시 병합하는 함수 mergeSort

const merge = (arr1, arr2) => {
  let result = []; // arr1과 arr2를 병합 정렬하여 반환할 새 배열
  let [i, j] = [0, 0]; // [pointerIndexOfArr1, pointerIndexOfArr2]

// 두 개의 포인터가 모두 각 배열의 길이보다 작을 때
  while (i < arr1.length && j < arr2.length) { 
    if (arr1[i] <= arr2[j]) {
      result.push(arr1[i]);
      i++;
    } else {
      result.push(arr2[j]);
      j++;
    }
  }

// arr1만 남았을 때
  while (i < arr1.length) {
    result.push(arr1[i]);
    i++;
  }

// arr2만 남았을 때
  while (j < arr2.length) {
    result.push(arr2[j]);
    j++;
  }

  return result;
};


const mergeSort = (arr) => {
	// arr의 길이가 1보다 작거나 같으면 이미 정렬된 배열(base case)
  if (arr.length <= 1) return arr; 
  let mid = Math.ceil(arr.length / 2); // arr의 중간 index
	// mid를 중심으로 left, right 배열로 나누고 각각 재귀함수를 통해 병합정렬
  let left = mergeSort(arr.slice(0, mid)); 
  let right = mergeSort(arr.slice(mid));
	// 최종적으로 정렬된 left와 right를 병합정렬
  return merge(left, right);
};

3. Big O

---

병합정렬에서는 예외 케이스 없이 최적/평균/최악 케이스 모두 시간 복잡도가 O(n log n)으로 나타난다.

처음 주어진 배열을 0 또는 1개 요소의 배열까지 나눌 때 log n이 된다.

8개의 요소가 있는 배열이 주어진다면 최소 배열까지 나누기 위해 3번의 단계가 필요하다

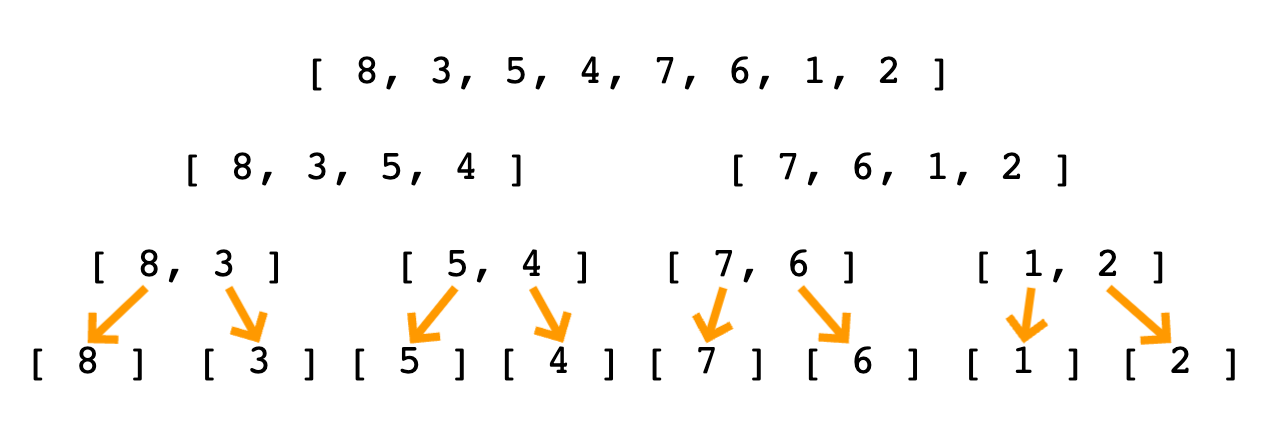
다시 합병될 때는 각각의 요소를 모두 확인하여 비교하게 되므로 n이 곱해져 최종적으로 n log n이 된다.

공간 복잡도는 배열의 크기가 커질수록 사용해야 하는 메모리 공간이 늘어나게 되므로 O(n)으로 나타난다.