[자료구조/알고리즘] 빅오표기법(Big-O notation)

이승혜·2021년 11월 2일

빅오표기법 알고리즘 자료구조

자료구조/알고리즘

목록 보기

1/1

빅오 표기법

대표적인 점근 표기법 중 하나
알고리즘의 최악의 경우 복잡도를 측정함
시간 및 알고리즘 공간 복잡도 분석을 위함

점근 표기법이란?
어떤 함수의 증가 양상을 다른 함수와의 비교로 표현하는 정수론과 해석학의 방법
알고리즘에 대한 성능과 효율성을 측정하기 위해 점근 표기법을 사용한다
대표적으로 대문자 O 표기법, 대문자 오메가 표기법, 대문자 세타 표기법, 소문자 o 표기법, 소문자 오메가 표기법이 있음
빅오 표기법에서 n은 입력의 개수를 나타냄

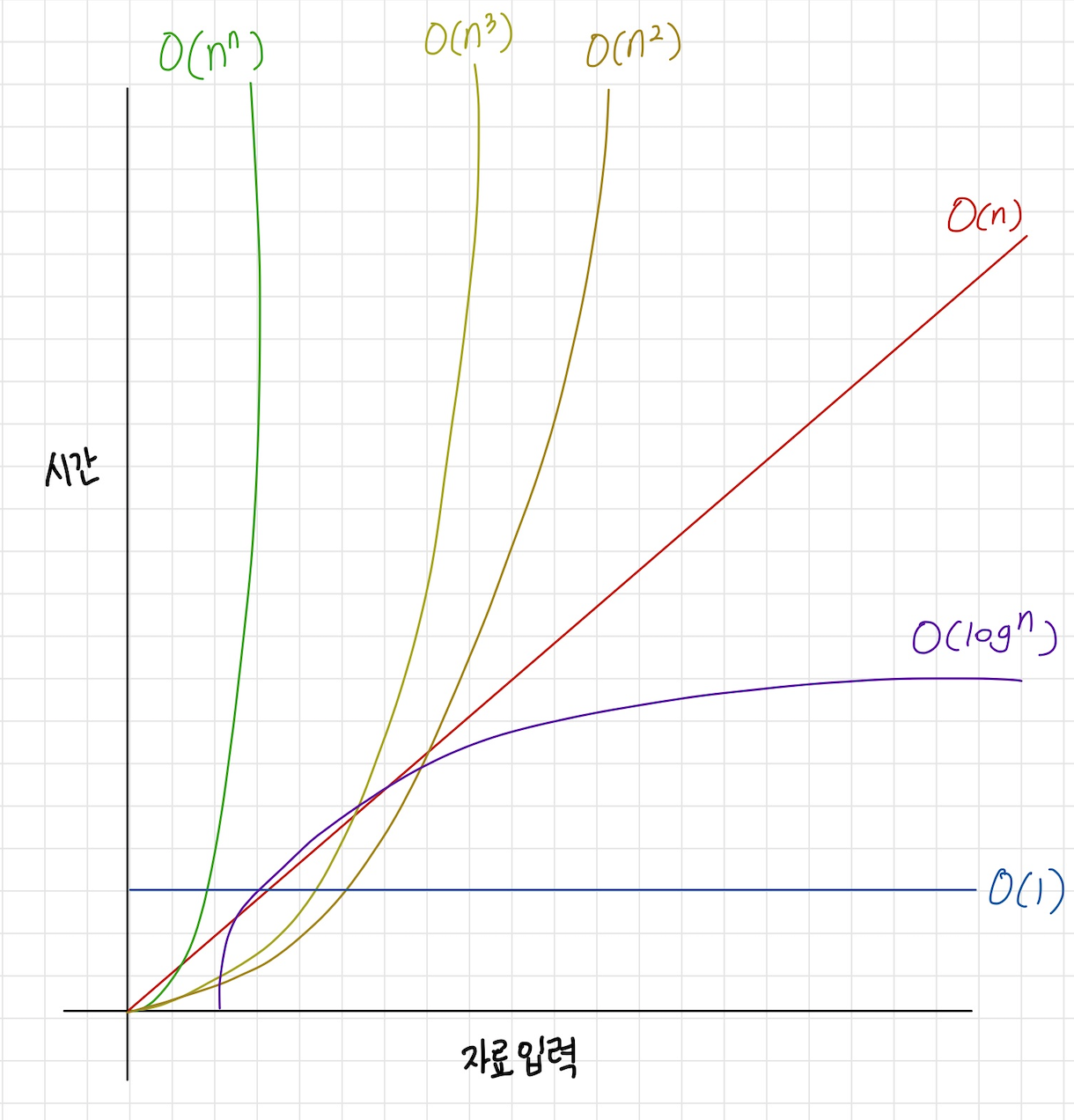▲ 일반적인 빅오 복잡도

일반적인 예

O(1)은 입력 공간에 대해 변하지 않는다
이를 상수 시간이라고 부른다
배열에 있는 항목을 인덱스를 사용해 접근하는 경우가 그 예다
O(n)은 선형 시간이고 최악의 경우에 n번의 연산을 수행해야 하는 알고리즘에 적용된다

❓선형
직선처럼 똑바른 도형, 또는 그와 비슷한 성질을 갖는 대상이라는 뜻으로, 이러한 성질을 갖고 있는 변환 등에 대하여 쓰는 용어이다
함수의 경우, 어떠한 함수가 진행하는 모양이 '직선' 이라는 의미로 사용
예를 들면, 입력된 숫자열의 총합을 계산하는 순서는 숫자열의 길이에 비례하는 시간이 필요함

O(n) 알고리즘의 예

function exampleLinear(n) {
  for (let i = 0; i < n; ++i) {
    console.log(i);
  }
}

exampleLinear(10);

// 출력결과
0
1
2
3
4
5
6
7
8
9

마찬가지로 O(n²)은 2차 시간이고 O(n³)은 3차 시간이다
2차 시간과 3차 시간 복잡도의 예는 다음과 같다

// 2차 시간 복잡도
function exampleQuadratic(n) {
  for (let i = 0; i < n; ++i) {
    console.log(i);
    for (let j = i; j < n; ++j) {
      console.log(j);
    }
  }
}

// 3차 시간 복잡도
function exampleCubic(n) {
  for (let i = 0; i < n; ++i) {
    console.log(i);
    for (let j = i; j < n; ++j) {
      console.log(j);
      for (let k = j; k < n; ++k) {
        console.log(k);
      }
    }
  }
}

로그 시간 복잡도를 지닌 알고리즘의 예는
2의 2승부터 n승까지의 항목들을 출력하는 경우이다

function exampleLogarithmic(n) {
  for (let i = 2; i <= n; i = i * 2) {
    console.log(i);
  }
}

exampleLogarithmic(1000000);

// 출력 결과
2
4
8
16
32
64
128
256
512
1024
2048
4096
8192
16384
32768
65536
131072
262144
524288

보는 것과 같이 로그 시간 복잡도의 효율은 백만 개의 항목과 같이
큰 입력이 있는 경우에 분명히 드러난다
n이 백만이라고 하더라도 log1,000,000은 19.9315686 이기 때문에 단지 19개의 항목만을 출력한다

빅오 표기법 규칙

계수 법칙
합의 법칙
곱의 법칙
전이 법칙
다항 법칙

계수 법칙: 상수를 제거하라

계수 법칙은 단순히 입력 크기와 연관되지 않은 상수를 전부 무시하는 것이다
빅오에서 입력 크기가 클 때 계수를 무시할 수 있다

상수 k > 0 인 경우 f(n)이 O(g(n))이면,
kf(n)은 O(g(n)이다.
이 말은 즉, 5f(n)과 f(n)이 모두 동일한 O(f(n))이라는 빅오 표기법을 지님을 의미한다

function a(n) {
  let count = 0;
  for (let i = 0; i < 5 * n; ++i) {
    count += 1;
  }
  return count;
}

console.log(a(10)); // 50

위 코드는 f(n)=5n이다
0부터 5n까지 실행하기 때문이다
하지만 이는 O(n)의 시간 복잡도를 가진다

n이 무한대 또는 아주 큰 수에 가까워질 때 연산이 추가적으로 존재한다고 해서 달라지는 것은 없기 때문이다
n이 충분히 클 때 위의 코드가 n번 수행된다고 할 수 있다
O(5n)은 O(n)과 같이 선형적으로 늘어나지만, 그 값이 5배일 뿐인거다

합의 법칙: 빅오를 더하라

합의 법칙은 시간 복잡도를 더할 수 있다는 것을 의미한다

f(n)이 O(h(n))이고 g(n)이 O(p(n))이라면
f(n)+g(n)은 O(h(n))+O(p(n))이다
이 때 주의해야할 점은 합의 법칙을 적용한 다음 계수 법칙을 적용해야한다는 점이다

function a(n) {
  let count = 0;
  for (let i = 0; i < n; ++i) {
    count++;
  }
  for (let i = 0; i < 5 * n; ++i) {
    count++;
  }
  return count;
}

첫 번째 반복문은 f(n)=n에 해당하고
두 번째 반복문은 f(n)=5n에 해당한다
이로 인해 결과값은 6n이지만 계수 법칙(상수 제거)을 적용하면 최종적인 결과는 O(n)=n이 된다

곱의 법칙: 빅오를 곱하라

곱의 법칙은 빅오가 어떤 식으로 곱해지는지에 관한 것이다

f(n)이 O(h(n))이고 g(n)이 O(p(n))이면
f(n)g(n)은 O(h(n)p(n))이다

function a(n) {
  let count = 0;
  for (let i = 0; i < n; ++i) {
    count++;
    for (let i = 0; i < 5 * n; ++i) {
      count++;
    }
  }
  return count;
}

위의 예에서 f(n)은 5n * n이다
내부 루프가 5n번 실행되고, 내부 루프가 외부 루프에 의해 n번 실행되기 때문이다
따라서 결과는 5n²번의 연산이 일어난다
계수 법칙을 적용하면 결과는 O(n)=n²

다항 법칙: 빅오의 k승

다항 법칙은 다항 시간 복잡도가 동일한 다항 차수를 지닌 빅오 표기법을 지님을 의미한다

f(n)이 k차 다항식이면 f(n)은 O(nᵏ)이다

function a(n) {
  let count = 0;
  for (let i = 0; i < n * n; ++i) {
    count++;
  }
  return count;
}

위의 예에서 f(n)=n²이다

쉽게 말해, 빅오 표기법은 제일 영향력 있는 것만 신경쓰겠다는 의미이다
(최고 차항을 남기고, 상수는 버린다)

O(30n³+20n²+500n+3000)로 표시된 값이 있을 때,
빅오 표기법은 제일 영향력 있는 것만 남겨 O(n³)으로만 표기한다

이 글은 📕자바스크립트로 하는 자료 구조와 알고리즘 책을 참고하여 작성하였습니다

이승혜

더 높이

[자료구조/알고리즘] 빅오표기법(Big-O notation)