코드

1) slice를 이용한 재귀

arr = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]

def mergesort(arr):
    if len(arr) < 2:
        return arr

    mid = len(arr)//2

    # 재귀할 때 마다 배열이 계속 생긴다.
    left_arr = mergesort(arr[:mid])
    right_arr = mergesort(arr[mid:])

    merge_arr = []
    l = r = 0
    while l < len(left_arr) and r < len(right_arr):
        if left_arr[l] < right_arr[r]:
            merge_arr.append(left_arr[l])
            l += 1
        else:
            merge_arr.append(right_arr[r])
            r += 1
            
    #남은 배열 이어 붙이기
    merge_arr += left_arr[l:]
    merge_arr += right_arr[r:]
    return merge_arr


print(mergesort(arr))

보기에는 편한 방법이지만 재귀를 진행하면서 left_arr , rigth_arr를 배열을 slicing 하면서 단계별 매번 생성하기 때문에 메모리 효율이 좋지 않다.

2) 병합결과를 담을 새로운 배열을 매번 생생시키지 않는 방법

arr = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]


def mergesort(arr):
    def sort(left, right):
        if right - left < 2:
            return
        mid = (left + right)//2
        sort(left, mid)
        sort(mid, right)
        merge(left, mid, right)

    def merge(left, mid, right):
        temp = []
        l, r = left, mid

        while l < mid and r < right:
            if arr[l] < arr[r]:
                temp.append(arr[l])
                l += 1
            else:
                temp.append(arr[r])
                r += 1

        # l,r 중 한배열은 모두 정렬됨 남는 것들 이어붙임
        while l < mid:
            temp.append(arr[l])
            l += 1
        while r < right:
            temp.append(arr[r])
            r += 1
        for i in range(left, right):
            arr[i] = temp[i-left]

    return sort(0, len(arr))


print(arr)
mergesort(arr)
print(arr)

→ 인덱스 접근을 통해 입력 배열을 계속해서 업데이트하면 메모리 사용량을 줄일 수 있다고 한다.

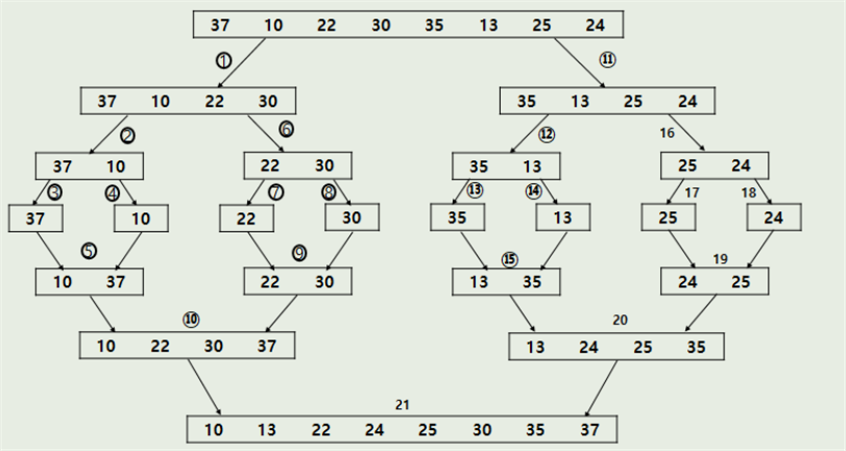
시간복잡도

각 층 수행된 비교횟수 = N
각 층 시간복잡도 = O(N)

총 배열 크기 N을 1/2 크기씩 나누고 크기 1일때 분할 중단한다.
2^K = N 라면 K개의 층이 생긴다는 것.
K = log(N)

총 시간 복잡도 = 층 개수 * 각 층 시간복잡도
= K * O(N)
= O(NlogN)

참고

https://www.daleseo.com/sort-merge/