2.1 삽입 정렬

1.

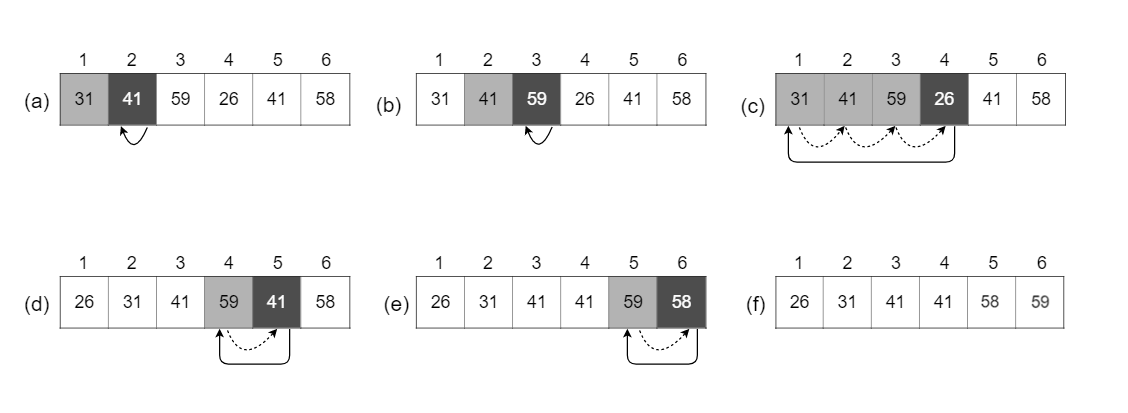
2.

INSERTION-SORT(A)
	for j = 2 to A.length
    key = A[j]
    i = j - 1
    while i > 0 and A[i] < key
    	A[i + 1] = A[i]
        i = i - 1
    A[i + 1] = key

3.

LINEAR-SEARCH(A, v)
	for i = 1 to A.length
    	if A[i] == v
        	return A[i]
    return NIL

루프 불변성은 루프가 돌기 위해 참이어야 하는 조건. 루프 불변성을 설정하는 방법은 다음과 같음.

1. 루프가 돌기 전 루프 불변성이 참이어야 한다.
2. 각 반복 후에도 불변 조건이 유지되어야 한다.
3. 루프가 종료될 때 불변 조건과 종료 조건이 결합되어 알고리즘의 타당성을 보이는 데 도움이 되어야 한다.

• 루프 불변성: 각 루프의 시작에서 부분배열 A[1.. i - 1]에는 v가 없다.

• 초기조건: 루프가 돌기 전(i = 1), 부분배열은 비어 있다. 따라서 불변성은 참이다.

• 유지조건: 루프가 돌면서, v와 A[i]가 같으면 i를 반환하고 알고리즘을 종료한다. v와 A[i]가 다르면 불변성은 참이다.

• 종료조건: i > A.length일때(모든 요소 탐색), 아직 v를 발견하지 못했으므로 NIL을 반환한다. 따라서 v가 없다는 것은 자명하므로, 알고리즘은 타당하다.

4.

입력: n비트로 표현된 이진수 정수를 저장하는 크기 n인 배열 A, B
출력: n+1비트를 저장하는 배열 C

ADD(A, B)
	carry = 0
    for i = 1 to A.length
    	sum = A[i] + B[i] + carry
        C[i] = sum % 2
        carry = sum / 2
    C[A.length + 1] = carry
    return C

2.2 알고리즘의 분석

1.

$O\left(n^{3}\right)$

2.

n = A.length
for i = 1 to n - 1
	min = A[i]
    for j + 1 to n
    	if min > A[j]
        	min = A[j]
    swap(min, A[i])

루프 불변성: 루프가 돌 때, 부분배열 A[1..i-1]은 가장 작은 원소들로 정렬되어 있다.

n-1개까지 바꾸면 되는 이유: n-1번의 반복 후, 부분배열 A[1..n-1]은 가장 작은 원소들로 정렬되어 있다. 따라서 n번째 원소는 가장 큰 값이다.

수행시간: $O\left(n^{2}\right)$

3.

배열의 크기가 n이라면, 최악의 경우 n번 탐색해야 하고, 평균적인 경우 n/2번 탐색해야 한다. 따라서 수행시간은 $O\left(n\right)$이다.

4.

특수 케이스를 갖도록 설정하고, 특수 케이스를 만족하면 알고리즘이 성공하도록 바꾼다.

2.3 알고리즘의 설계

1.

[3][41][52][26][38][57][9][49]
[3, 41][26, 52][38, 57][9, 49]
[3, 26, 41, 52][9, 38, 49, 57]
[3, 9, 26, 38, 41, 49, 52, 57]

2.

3.

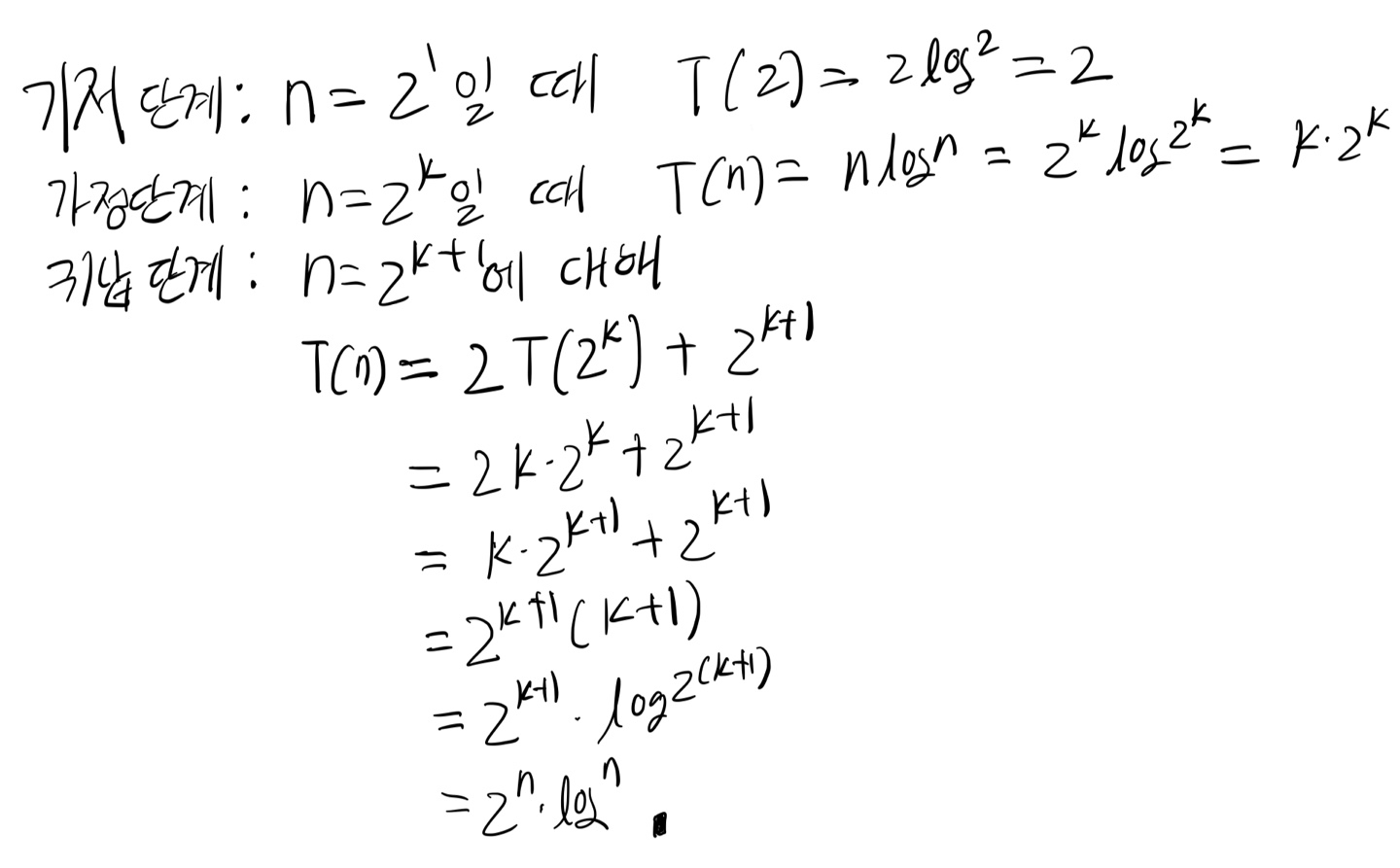
4.

$T(n)=T(n-1)+O(n)$

5.

BS(A, low, high, v)
	if(low > high)
    	return NIL
    mid = floor((low + high) / 2)
    if A[mid] == v
    	return mid
    else if A[mid] > v
    	return BS(A, low, mid - 1, v)
    else
    	return BS(A, mid + 1, high, v)