기본 알고리즘

알고리즘 공부 전 기본 상식 이해하기

- 회귀계수 (Regression Coefficient)
정의: 회귀계수는 각 독립변수(입력값)가 종속변수(결과값)에 미치는 영향을 나타내는 숫자
예시: 예를 들어, 키와 몸무게의 관계를 분석할 때, 키의 회귀계수가 0.5라면, 키가 1cm 증가할 때 몸무게가 평균적으로 0.5kg 증가한다는 의미야.
- 가중치 (Weight)
정의: 가중치는 회귀계수와 비슷하지만, 머신러닝에서는 좀 더 일반적인 용어로 사용돼. 독립변수에 곱해져서 그 변수가 종속변수에 미치는 영향을 조정
관계: 즉, 회귀계수는 특정 상황에서의 가중치라고 볼 수 있어.
- 편향 (Bias)
정의: 편향은 모델이 예측할 때 항상 더해지는 기본값이야. 모델이 항상 특정 값을 기준으로 시작하게 만드는 역할을 해.
예시: 만약 편향이 2라면, 모든 예측에 2를 더하는 것과 같아.

최선의 가중치와 편향을 찾는 이유

• 정확한 예측: 독립변수의 최선의 가중치와 편향을 찾으면 모델이 훈련 데이터에 대해 더 정확한 예측을 할 수 있어.
• 일반화: 좋은 가중치와 편향을 찾으면 새로운 데이터에도 잘 작동하게 돼, 즉 모델이 과대적합되지 않도록 도와줘.
• 패턴 이해: 각 독립변수가 종속변수에 미치는 영향을 파악함으로써, 데이터의 숨은 패턴을 이해할 수 있어.

linear Regression

최선 회귀모델은 오차합이 최소가 되는 모델 의미

단순회귀
독립변수가 하나. -> x값 하나만으로 y값 설명
• 𝑦=𝑤0+𝑤1𝑥1

 # 회귀계수 확인
print(model.coef_) #회귀계수(가중치), 독립변수에 곱해지는 값
 print(model.intercept_) # 편향
 
 ex)  𝑦 =−15.81+3.92∙𝑥   #편항 - 15.81, 가중치 3.92

다중회귀
독립변수 여러 개 -> y값 설명을 위해 여러 x필요

• 𝑦=w0+w1𝑥1+w2𝑥2+w3𝑥3+⋯+w𝑛𝑥n
• 각 독립변수의 최선의 가중치와 편향(w0)을 찾음.

# 회귀계수 확인
print(list(x_train)) #회귀계수가 여럿이므로 독립변수 이름 확인
 print(model.coef_) #가중치
 print(model.intercept_) 평균
 
 ex) 𝑂𝑧𝑜𝑛𝑒 = −53.37+1.52∙𝑇𝑒𝑚𝑝−3.57∙𝑊𝑖𝑛𝑑 +0.07∙𝑆𝑜𝑙𝑎𝑟.R

linear Regression알고리즘은 회귀모델에만 사용가능

 # 불러오기
from sklearn.linear_model import LinearRegression
 from sklearn.metrics import mean_absolute_error, r2_score
 # 선언하기
model = LinearRegression()
 # 학습하기
model.fit(x_train, y_train)
 # 예측하기
y_pred = model.predict(x_test)
 # 평가하기
print(mean_absolute_error(y_test, y_pred))
 print(r2_score(y_test, y_pred))

K-Nearest Neighbor (knn)

학습용 데이터에서 k개의 최근접 이웃을 찾아 그 값들로 새로운 값 예측 알고리즘.
회귀 & 분류 모두 사용됨, 간단함. (연산속도는 느림)

• k개의 값의 평균을 계산해 값 예측
• 가장 많이 포함된 유형으로 분류

k값의 중요성
k값에 따라 예측값이 달라짐, 적절 k값 찾기 중요(기본값 = 5)
일반적으로
• k를 1로 설정 안함! → 이웃 하나로 현재 데이터를 판단하기엔 너무 편향된 정보
• k 홀수로 설정 ! → 짝수일 경우 과반수 이상의 이웃이 나오지 않을 수 있음.

스케일링 방법

스케일링 여부에 따라 knn모델 성능이 달라질 수 있음.
knn에 꼭 필요한 스케일링!!!

정규화 : 각 변수 값이 0과 1사이

표준화 : 각 변수 평균이 0, 표준펴차가 1

 # 함수 불러오기
from sklearn.preprocessing import MinMaxScaler
 # 정규화
scaler = MinMaxScaler()
 scaler.fit(x_train)
 x_train = scaler.transform(x_train)
 x_test = scaler.transform(x_test)
 
# 평가용 데이터에도 학습용 데이터 기준으로 스케일링 수행함.

회귀모델 구현

  # 불러오기
from sklearn.neighbors import KNeighborsRegressor
 from sklearn.metrics import mean_absolute_error, r2_score
 # 선언하기
model = KNeighborsRegressor(n_neighbors=5)
 # 학습하기
model.fit(x_train, y_train)
 # 예측하기
y_pred = model.predict(x_test)
 # 평가하기
print(mean_absolute_error(y_test, y_pred))
 print(r2_score(y_test, y_pred))

분류모델 구현

# 불러오기
from sklearn.neighbors import KNeighborsClassifier
 from sklearn.metrics import confusion_matrix, classification_report
 # 선언하기
model = KNeighborsClassifier(n_neighbors=5)
 # 학습하기
model.fit(x_train, y_train)
 # 예측하기
y_pred = model.predict(x_test)
 # 평가하기
print(confusion_matrix(y_test, y_pred))
 print(classification_report(y_test, y_pred))

Decision Tree(의사결정 나무)

특정 변수에 대한 의사결정 규칙을 나무가지가 뻗는 형태로 분류
분류 & 회귀 모두 사용
분석 과정이 직관적
분석과정을 실제 눈으로 확인 가능 -> 화이트 박스 모델
*트리 깊이를 제한하는 튜닝 필요

분류모델의 경우 마지막 노드에 있는 샘플들의 최빈값을 예측값을 반환(불순도)
회귀모델의 경우 마지막 노드에 있는 샘플들의 평균을 예측값을 반환(mse)

불순도 ?
순도의 반대말
순도가 높을 수록 분류가 잘된 것

수치화 지표

• 지니불순도
• 엔트로피

Logisitic Regression

분류모델에서만 사용가능

# 불러오기
from sklearn.linear_model import LogisticRegression
 from sklearn.metrics import confusion_matrix, classification_report
 # 선언하기
model = LogisticRegression()
 # 학습하기
model.fit(x_train, y_train)
 # 예측하기
y_pred = model.predict(x_test)
 # 평가하기
print(confusion_matrix(y_test, y_pred))
 print(classification_report(y_test, y_pred))

svm

support vector machine

데이터 분류를 위한 기준선, 결정 경계선을 찾는 알고리즘.
분류 및 회귀 문제 모두 사용가능

• 분류 문제를 위한 관점에서 학습 요약해볼게요 !

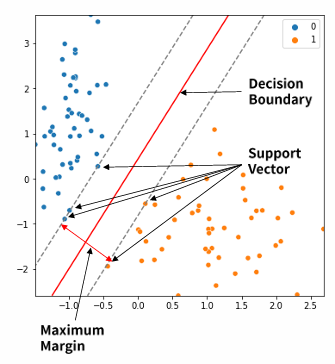
결정 경계? decision boundary
-서로 다른 분류값 결정하는 경계

벡터?
-2차원 공간 상에 나타난 데이터 포인트
서포트 벡터
-결정 경계선과 가장 가까운 데이터 포인트

마진 maximum margin
-결정경계와 서포트 벡터 사이의 거리
-마진이 클수록 새로운 데이터에 대해 안정적 분류 가능성 높음
-분류가 잘 되었다는 뜻
*혹, 학습시 분류가 잘못되었더라도 마진이 크다면 실제 테스트 및 운영시 새로운 데이터에 대한 분류가 안정적일 것 !

+학습시 에러 적은 모델보다 운영시 에러 적은 모델이 good(당연한 말)
svc는 약간의 오류 허용을 위해 비용(c)변수를 사용함.
c를 낮게 잡으면?
-마진을 높이고 에러를 증가시키는 경계선을 만듦 -> 과소적합

c를 높게 잡으면?
-마진을 낮추고 에러를 감소시키는 경계선을 만듦 -> 과대적합

=> 적절한 비용값 C를 찾는 것이 매우 중요

• SVM은 직선 OR 초평면으로 분류하는 방식, 즉 선형 분류기
  선형으로 분류할 수 없는 데이터 셋이 더 많음.
  때문에 직선으로 분류하면 오차가 커지기도 함.

커널 트릭

매핑함수

• 저차원 데이터를 고차원으로 옮겨주는 함수
• 대량 데이터를 저차원에서 고차원으로 옮기려면 계산량 많아 사용 어려움

커널트릭

• 데이터를 실제로 고차원으로 옮기지 X, 옮긴 것 같은 효과를 주어 결정 경계선을 빠르게 찾는 방법

데이터 분류를 위한 결정 경계선을 찾는 알고리즘 SVM
회귀모델 구현

# 불러오기
from sklearn.svm import SVR
 from sklearn.metrics import mean_absolute_error, r2_score
 # 선언하기
model = SVR(kernel='linear', C=1)
 # 학습하기
model.fit(x_train, y_train)
 # 예측하기
y_pred = model.predict(x_test)
 # 평가하기
print(mean_absolute_error(y_test, y_pred))
 print(r2_score(y_test, y_pred)

분류모델 구현

 # 불러오기
from sklearn.svm import SVC
 from sklearn.metrics import confusion_matrix, classification_report
 # 선언하기
model = SVC(kernel='linear', C=1)
 # 학습하기
model.fit(x_train, y_train)
 # 예측하기
y_pred = model.predict(x_test)
 # 평가하기
print(confusion_matrix(y_test, y_pred))
 print(classification_report(y_test, y_pred))

K-Fold Cross Validation

k 분할 교차 검증
k-분할 교차 검증은 데이터를 k개의 부분으로 나눈 후, 각 부분을 한 번씩 테스트 데이터로 사용하고 나머지를 훈련 데이터로 사용하는 방법

단계별 설명
데이터 나누기:
전체 데이터를 k개의 같은 크기의 그룹으로 나눠. 예를 들어, 데이터가 100개라면, k를 5로 설정하면 20개의 데이터로 구성된 5개의 그룹이 만들어져.
모델 훈련과 테스트:

1번째 단계: 첫 번째 그룹(20개)을 테스트 데이터로 사용하고, 나머지 80개로 모델을 훈련해.
2번째 단계: 두 번째 그룹을 테스트 데이터로 사용하고, 나머지 80개로 모델을 훈련해.
이 과정을 k번 반복해. 즉, 각 그룹이 한 번씩 테스트 데이터로 사용돼.
성능 평가:

각 반복에서 모델의 성능(예: 정확도, F1 점수 등)을 기록해.
k번의 성능 평가 결과를 평균내서 최종 성능 점수를 얻어.

단, k는 2 이상 되어야함.

 # 1단계: 불러오기
from sklearn.tree import DecisionTreeClassifier
 from sklearn.model_selection import cross_val_score
 # 2단계: 선언하기
model = DecisionTreeClassifier(max_depth=3)
 # 3단계: 검증하기, cv = 기본 분할 개수 값
cv_score = cross_val_score(model, x_train, y_train, cv=10)
 # 확인
print(cv_score)
 print(cv_score.mean())

하이퍼파라미터(hyperparameter) 튜닝

머신러닝 모델의 성능을 조정하는 설정값

grid search, random search

KKN 알고리즘 경우 K 값, 즉 n_neighbors 옵션 값을 어떻게 설정하냐에 따라 모델 성능이 달라짐.

최선의 n_neighbors 옵션 값 설정이 요구됨.

생각 할 수 있는 방법 1 [grid search]

1~n까지의 정수를 n_neighbors 옵션 값으로 해서 수집
수집 정보에서 성능 좋은 n_neighbors 옵션 값 찾음
n_neighbors 옵션 값을 갖는 KKN모델을 선언해 학습, 예측, 평가

-> n값이 크면 소요 시간 多

생각 할 수 있는 방법 2 [random search]
1~n까지의 정수를 무작위 m개 골라 n_neighbors 옵션 값으로 해서 수집
수집 정보에서 성능 좋은 n_neighbors 옵션 값 찾음
n_neighbors 옵션 값을 갖는 KKN모델을 선언해 학습, 예측, 평가

-> 임의 m개만 골라 수행하여 소요 시간 少
but, 선택되지 못한 값에 좋은 성능의 값이 있을까봐 걱정이 됨.

 # 파라미터 하나의 경우
param = {'n_neighbors': range(1, 101)}

n_neighbors값이 1부터 100까지 설정되면서 성능을 확인
grid search의 경우 100번 수행되면서 모든 경우의 성능 확인
random search의 경우 지정한 개수 임의 값에 대해서 성능 확인

 # 파라미터 두 개 경우
param = {'n_neighbors': range(1, 101), 
'metric': ['euclidean', 'manhattan']}

#유클리드 거리 (euclidean): 두 점 간의 직선 거리를 측정해.
#맨해튼 거리 (manhattan): 두 점 사이의 수평과 수직 거리의 합을 측정해.

n_neighbors값이 100, metic이 2개 -> 200개 조합 생성
grid search의 경우 200번 수행되면서 모든 경우의 성능 확인
random search의 경우 지정한 개수 임의의 조합에 대해서 성능 확인

grid search

 # 함수 불러오기
from sklearn.neighbors import KNeighborsClassifier
 from sklearn.model_selection import GridSearchCV
 # 파라미터 선언
param = {'n_neighbors': range(1, 500, 10), 'metric': ['euclidean', 'manhattan']}
 # 기본모델 선언
knn_model = KNeighborsClassifier()
 # Grid Search 선언
model = GridSearchCV(knn_model, param, cv=3)

지정 값에 대해 최적의 하이퍼파라미터 값을 찾아줌,
넓은 범위와 큰 step으로 설정 후 범위 좁혀나가며 시간 단축

random search

# 함수 불러오기
from sklearn.neighbors import KNeighborsClassifier
 from sklearn.model_selection import RandomizedSearchCV

 # 파라미터 선언
param = {'n_neighbors': range(1, 500, 10), 
'metric': ['euclidean', 'manhattan']}
 # 기본모델 선언
knn_model = KNeighborsClassifier()
 # Random Search 선언
model = RandomizedSearchCV(knn_model,
 param,
 cv=3,               
n_iter=20

 # 학습하기
model.fit(x_train, y_train)

 # 수행 정보
model.cv_results_
 # 최적 파라미터
model.best_params_
 # 최고 성능
model.best_score_