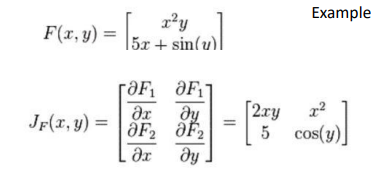vector_backprop
- 스칼라끼리의 관계가 있고 백터와 스칼라의 관계는 Gradient, 벡터와 벡터간의 관계를 jacobian이라 함
Jacobian
- 벡터와 벡터간의 관계를 정의
- 위쪽의 1x2의 벡터에서 2개의 행에 각각 x,y가 관여하는 점을 정리
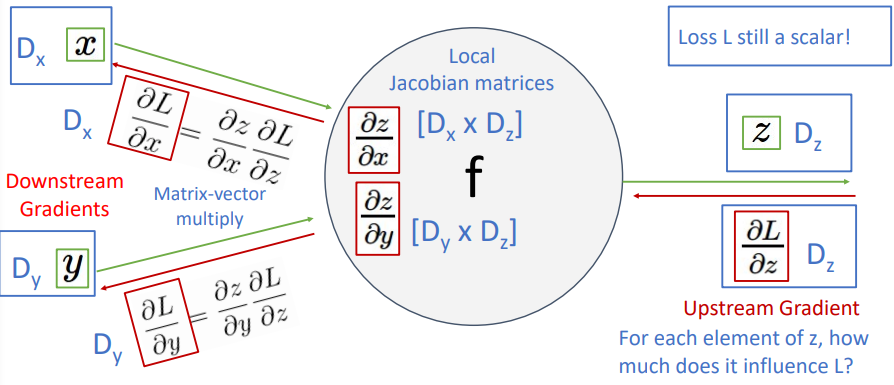
- f에서 z는 결국 x와 y의 연산의 결과, Backpropagation은 x,y가 그 단계에서 z에 각각 얼마나 영향을 주었는지 구하는 것
- upstream에서 주어진 그레디언트를 가지고 자코비안으로 local 그레디언트를 구해서
- downstream으로 체인룰을 거쳐 흘려보내줌
- 이때 차원도 x,y,z에 맞게 나옴

- upstream의 미분값은 주어지고
- local 자코비안은 upstream에대한 인풋에 미분
- 1보다 크면 1 작으면 0

- local 자코비안은 upstream에대한 인풋에 미분
- 자코비안 행렬에 업스트림에서 주어진 그레디언트를 곱해서 다운스트림으로 흘려주는 것
행렬의 연산

- 데이터가 N개 들어왔을떄의 경우
- 결국 행렬의 크기에서 다운스트림과 인풋의 크기가 같아야하고 업스트림과 아웃풋의 크기가 같아야함
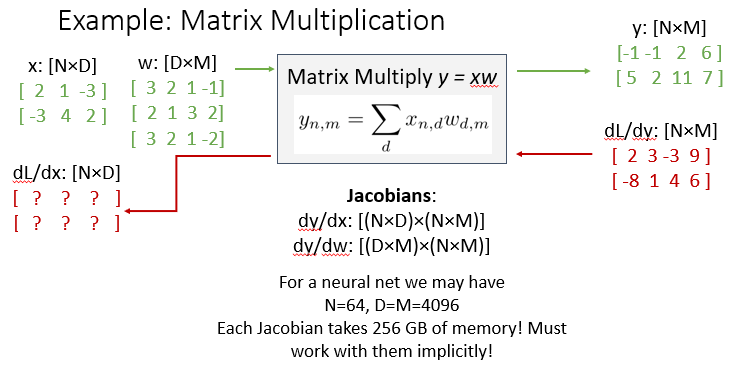
- 하지만 위의 경우는 연산횟수가 너무 많음(저장공간도 많이 사용)
- 그래서 중간에 자코비안을 거치지 않고 바로 다운스트림을 구하는 룰을 찾을것
- 그래서 다운 스트림(dL/dx)의 [1][1]을 구하려면?
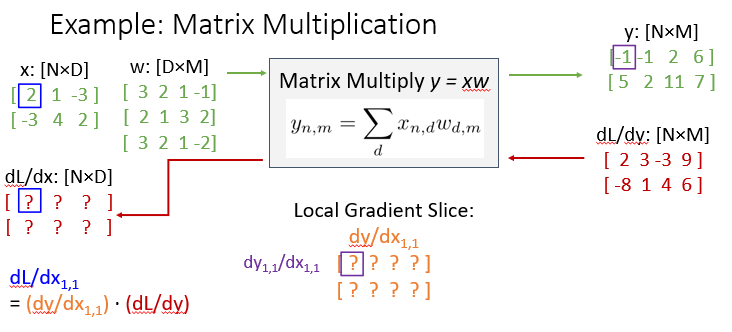
- 인풋(dx)의 [1][1]만 사용
- 먼저 dy/dx[1][1]을 구함
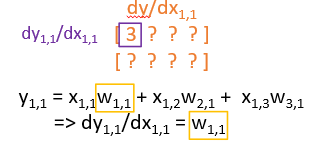
- dy/dx[1][1]은 결국 dx[1][1]과 연관된(dx[1][1]을 사용하는) 부분만 들어가게 됨

- dw에서 dx[1][1]을 사용하는 부분만 그대로 들어가는 결과
- 그 후 dl/dx[1][1]을 위해 위에서 구한 dy/dx[1][1]에 업스트림 dl/dy를 곱함

- 행렬 곱셈 아니고 같은 자리끼리 곱하는거

일반화
- dx[1][1]에서 인덱스가 바뀌어도 똑같이 dx[1][1]이 관여하는 값만 살아나고 나머지는 0이됨(일반화 가능)
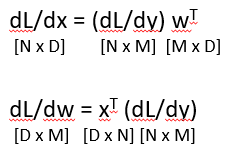

- 행렬곱하기 위해 w와x를 트렌스포즈하고 각각 앞,뒤에 곱함