
아이디어
문제 분류가 이진탐색(이분탐색)으로 되어있다.
분류를 보지 못했어도, 문제의 제한사항에서 n과 times의 크기가 지나치게 크기 때문에 이진탐색을 사용해야함을 알 수 있다.
그렇다면 이진탐색에서 어떤 것을 기준으로 삼아야 할까?
문제의 예시처럼, times=[7,10] 라고 가정하자.
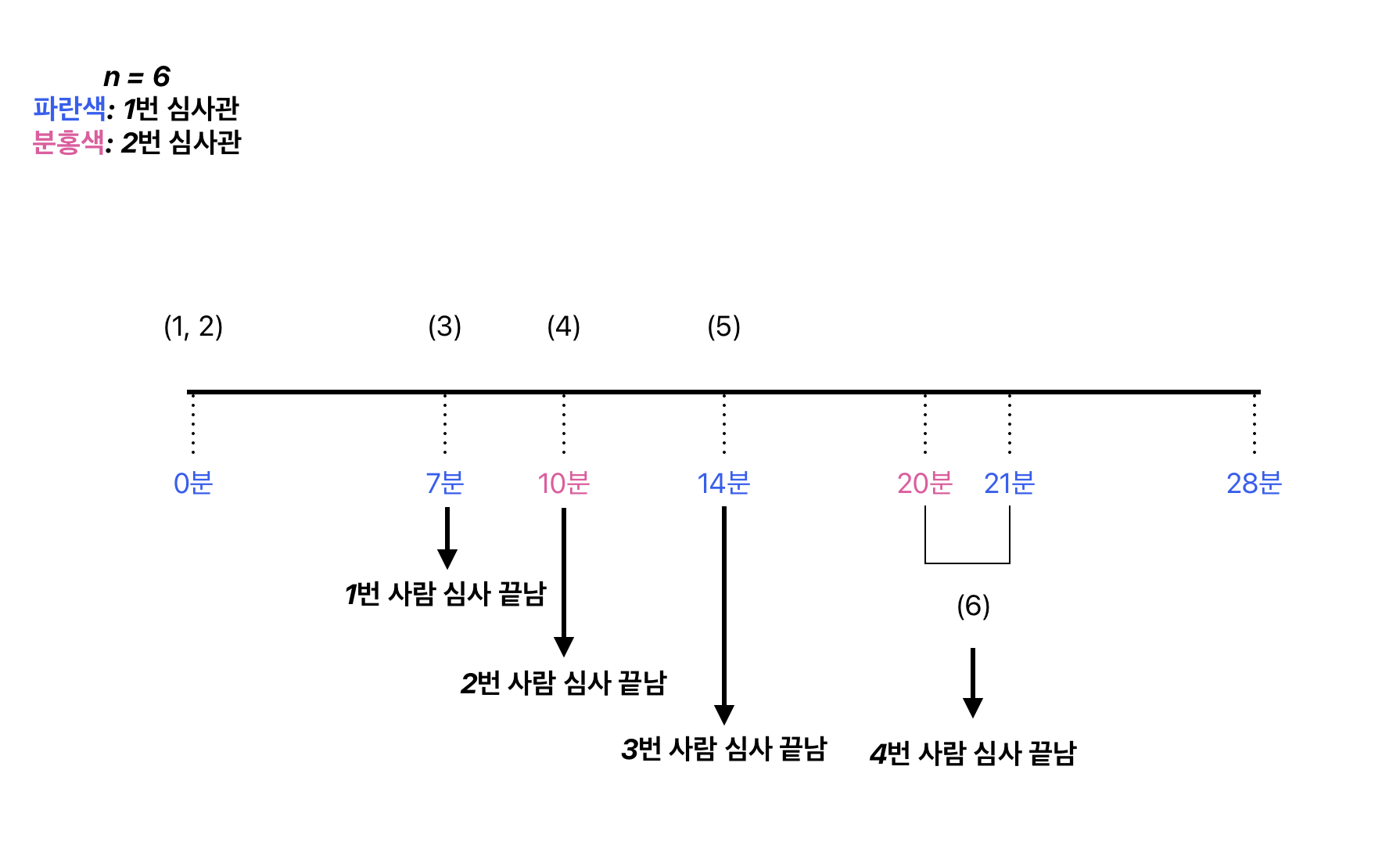
그림을 보면 특정 시간까지 심사할 수 있는 사람의 수가 달라진다.
예를 들어, 현재 15분이라면... 심사의 [시작, 끝]은 다음과 같다.
- 소요 시간 7분 심사관이 2명을 심사한다.(
[0, 7],[7, 14]) - 소요 시간 10분 심사관이 1명을 심사한다.(
[0, 10])
특정 시간마다 심사할 수 있는 사람의 수가 달라지므로, 시간을 기준으로 설정했다.
(그 외 세부 로직은 떠오르지가 않아, 아래부터는 다른 사람의 포스팅을 참고했다.)
자, 우리가 구하고자 하는 것은 "모든 사람이 심사를 받는데 걸리는 시간의 최솟값"이다.
어떻게 하면 이 최솟값을 구할 수 있을까?
만약 현재 시간이 30분이고, 6명을 심사해야 한다고 가정해보자.
가능한 경우의 수는 다음과 같다.
- 7분 심사관이 3명, 10분 심사관이 3명 →
max(7 * 3, 10 * 3) = 30분 - 7분 심사관이 4명, 10분 심사관이 2명 →
max(7 * 4, 10 * 2) = 28분
즉, 심사에 소요되는 시간이 적은 심사관이 더 많은 사람을 심사하면 소요시간이 최솟값이 될 수 있다.
심사에 소요되는 시간이 적은 심사관이 더 많은 사람을 심사 하면 총 소요시간이 적어진다는 것은 너무나 당연한데 왜 생각을 못했을까..
코드
def solution(n, times):
answer = 0
l, r = 1, max(times) * n
while l <= r:
mid = l + (r - l) // 2
total = 0 # 총 심사한 사람 수
# 각 심사관이 심사한 사람의 수 더하기
for time in times:
total += mid // time
# 주어진 n명보다 같거나 더 많은 사람을 심사했다.
# 더 적은 사람을 탐색해야 한다. → 소요 시간을 줄여야 한다. → mid를 줄여야 한다.
if total >= n:
r = mid - 1 # 왼쪽 부분 탐색
answer = mid
# 주어진 n명보다 더 적은 사람을 심사했다.
# 더 많은 사람을 탐색해야 한다. → mid를 늘려야 한다.
else:
l = mid + 1 # 오른쪽 부분 탐색
return answer풀이
먼저, 포인터의 초기 값은 다음과 같다.
l:1(/분)r:max(times) * n/(분)→심사 소요시간이 제일 긴 심사관이 n명을 심사하는데 걸리는 시간
mid를 설정하고, 총 심사관이 심사한 사람의 수를 구한다.
for time in times:
total += mid // time✅ 헷갈렸던 것
time이 7이고 mid가 14일 때 심사를 몇 분부터 시작하는 것이고, 심사한 사람의 수가 2명인가 3명인가?
문제를 보면, 0분 부터 심사는 시작이 가능하다.
따라서,
- 0분 시작 ~ 7분 끝 : 1명
- 7분 시작 ~ 14분 끝: 1명
처음에, 0분, 7분, 14분으로 총 3명이 가능하지 않나? 라고 생각했는데, 14분은 심사의 끝이 아닌 심사의 시작을 의미하므로 21분에 심사가 끝이난다.
따라서, 14분 이내에 포함되지 못하므로 심사를 완료한 사람의 수에서는 제외된다.
총 심사한 사람의 수를 구했다면, 주어진 n명과 비교를 해본다.
if total >= n:
r = mid - 1 # 왼쪽 부분 탐색
answer = mid
else:
l = mid + 1 # 오른쪽 부분 탐색- 총 심사한 사람의 수가
n명보다 같거나 크다?- 이는
mid를 너무 크게 잡아서 발생한다. 따라서,mid를 줄인다.(= 왼쪽 부분 탐색)
- 이는
- 총 심사한 사람의 수가
n명보다 작다?- 이는 mid를 너무 작게 잡아서 발생한다. 따라서,
mid를 늘린다.(= 오른쪽 부분 탐색)
- 이는 mid를 너무 작게 잡아서 발생한다. 따라서,

