[프로그래머스/Lv.3] - 미로 탈출 명령어

ZenTechie·2023년 5월 8일

PS

목록 보기

14/53

처음에 문자열이 사전 순으로 가장 빠른 경로로 탈출 해야 한다는 조건에서, 최소 횟수를 찾을 때 사용하는 BFS를 생각했다.

후에 생각난건데, 사전 순으로 가장 빠르다는 것은 최소 횟수랑은 연관이 없다.
사전 순으로 가장 빠른 것은, 초기에 방향 리스트(dx, dy)를 초기화 할 때 설정하면 되는 것이다.

문제

n x m 격자 미로가 주어집니다. 당신은 미로의 (x, y)에서 출발해 (r, c)로 이동해서 탈출해야 합니다.

단, 미로를 탈출하는 조건이 세 가지 있습니다.

격자의 바깥으로는 나갈 수 없습니다.
(x, y)에서 (r, c)까지 이동하는 거리가 총 k 여야 합니다. 이때, (x, y)와 (r, c)격자를 포함해, 같은 격자를 두 번 이상 방문해도 됩니다.
미로에서 탈출한 경로를 문자열로 나타냈을 때, 문자열이 사전 순으로 가장 빠른 경로로 탈출해야 합니다.
이동 경로는 다음과 같이 문자열로 바꿀 수 있습니다.

l: 왼쪽으로 한 칸 이동
r: 오른쪽으로 한 칸 이동
u: 위쪽으로 한 칸 이동
d: 아래쪽으로 한 칸 이동
예를 들어, 왼쪽으로 한 칸, 위로 한 칸, 왼쪽으로 한 칸 움직였다면, 문자열 "lul"로 나타낼 수 있습니다.

미로에서는 인접한 상, 하, 좌, 우 격자로 한 칸씩 이동할 수 있습니다.

예를 들어 다음과 같이 3 x 4 격자가 있다고 가정해 보겠습니다.

....
..S.
E...

미로의 좌측 상단은 (1, 1)이고 우측 하단은 (3, 4)입니다. .은 빈 공간, S는 출발 지점, E는 탈출 지점입니다.

탈출까지 이동해야 하는 거리 k가 5라면 다음과 같은 경로로 탈출할 수 있습니다.

lldud
ulldd
rdlll
dllrl
dllud
...

이때 dllrl보다 사전 순으로 빠른 경로로 탈출할 수는 없습니다.

격자의 크기를 뜻하는 정수 n , m , 출발 위치를 뜻하는 정수 x , y , 탈출 지점을 뜻하는 정수 r , c , 탈출까지 이동해야 하는 거리를 뜻하는 정수 k 가 매개변수로 주어집니다. 이때, 미로를 탈출하기 위한 경로를 return 하도록 solution 함수를 완성해주세요. 단, 위 조건대로 미로를 탈출할 수 없는 경우 "impossible"을 return 해야 합니다.

제한 사항

2 ≤ n (= 미로의 세로 길이) ≤ 50
2 ≤ m (= 미로의 가로 길이) ≤ 50
1 ≤ x ≤ n
1 ≤ y ≤ m
1 ≤ r ≤ n
1 ≤ c ≤ m
(x, y) ≠ (r, c)
1 ≤ k ≤ 2,500

입출력 예

n	m	x	y	r	c	k	result
3	4	2	3	3	1	5	"dllrl"
2	2	1	1	2	2	2	"dr"
3	3	1	2	3	3	4	"impossible"

입출력 예 설명

입출력 예 #1

문제 예시와 동일합니다.

입출력 예 #2

미로의 크기는 2 x 2입니다. 출발 지점은 (1, 1)이고, 탈출 지점은 (2, 2)입니다.

빈 공간은 . , 출발 지점을 S , 탈출 지점을 E 로 나타내면 다음과 같습니다.

S.
.E

미로의 좌측 상단은 (1, 1)이고 우측 하단은 (2, 2)입니다.

탈출까지 이동해야 하는 거리 k가 2이므로 다음과 같은 경로로 탈출할 수 있습니다.

"dr" 이 사전 순으로 가장 빠른 경로입니다. 따라서 "dr" 을 return 해야 합니다.

입출력 예 #3

미로의 크기는 3 x 3입니다. 출발 지점은 (1, 2)이고, 탈출 지점은 (3, 3)입니다.

빈 공간은 . , 출발 지점을 S , 탈출 지점을 E로 나타내면 다음과 같습니다.

.S.
...
..E

미로의 좌측 상단은 (1, 1)이고 우측 하단은 (3, 3)입니다.

탈출까지 이동해야 하는 거리 k 가 4입니다. 이때, 이동 거리가 4이면서, S 에서 E 까지 이동할 수 있는 경로는 존재하지 않습니다.

따라서 "impossible" 을 return 해야 합니다.

고민한 점

처음에 문자열이 사전 순으로 가장 빠른 경로로 탈출, 좌표 상의 이동하는 문제여서 BFS를 생각했지만,
조건 처리를 할 때 dfs가 더 편할 것 같아, DFS로 풀기로 했다.

사전 순으로 가장 빠른 경로로 탈출에 부합하기 위해서 모든 경로를 set에 저장해야겠다고 생각했다.
(예전에 파이썬에서 문자열 비교가 가능한지 찾아봤을 때 '>', '<' 연산이 사용이 안된다고 봤던 기억이 있었다.)

그리고, 문제에서 상, 하, 좌, 우 는 'u', 'd', 'l', 'r' 로 표현했다.

문자열을 사전 순으로 가장 빠르게 정렬하려면, 가장 앞에 나오는 문자가 사전 순으로 가장 빠른 문자여야 한다. 즉, 이동을 시작할 때부터 가장 빠른 문자로 이동해야 한다.

따라서, 'd', 'l', 'r', 'u' 순서로 재귀호출을 진행했다.
('d' 부터 시작한다고 해서, S 의 행이 E 의 행보다 클 때 문제가 생기지는 않는다. 왜냐하면, 어차피 모든 경우의 수를 확인하는 백트래킹이기 때문이다.)

문제에서 눈여겨 봐야할 키워드

문자열이 사전 순으로 가장 빠른 경로로 탈출
(x, y) 와 (r, c) 를 포함해 같은 격자를 두 번 이상 방문해도 된다.
(x, y) 에서 (r, c) 까지 이동하는 거리가 총 k여야 한다.

처음 접근 - TLE

from collections import deque
import sys
sys.setrecursionlimit(5000)
# 격자의 크기 n, m 
# 출발 위치 x, y
# 탈출 위치 r, c
# 탈출까지 이동해야 하는 거리 k
# dx, dy = [-1, 1, 0, 0], [0, 0, -1, 1] # 상, 하, 좌, 우
def solution(n, m, x, y, r, c, k):
    ret = set() # 이동 거리가 K인 경로를 저장하는 집합
    
    def dfs(x, y, r, c, way, dist):
    	# 범위 확인
        if x < 1 or x > n or y < 1 or y > m: return
    
        if dist == k: # 이동한 거리가 K이고
            if x == r and y == c: # 목적지 도착했다면
                ret.add(way)
            return
        
        dfs(x + 1, y, r, c, way + "d", dist + 1) # 하
        dfs(x, y - 1, r, c, way + "l", dist + 1) # 좌
        dfs(x, y + 1, r, c, way + "r", dist + 1) # 우
        dfs(x - 1, y, r, c, way + "u", dist + 1) # 상
        
        
    dfs(x, y, r, c, "", 0)
    
    if not ret: return "impossible" # 경로가 없다면
    answer = sorted(ret)[0] # 사전 순으로 정렬하고, 맨 앞의 경로를 뽑아낸다.
    return answer

꽤나 간단하게 풀 수 있겠다고 생각하고 작성했는데, 결과는 처참했다.

시간복잡도 : $O(4^k)$ → 시간초과

채점 결과

정확성 : 16.3
합계 : 16.3 / 100.0
(테스트 케이스 4, 5, 6, 7, 8 제외 전부 시간초과)

최종 접근

from collections import deque
import sys
sys.setrecursionlimit(10 ** 6)

dx, dy = [1, 0, 0, -1], [0, -1, 1, 0] # 하, 좌, 우, 상
alp = ["d", "l", "r", "u"]
answer = 'z' # 사전 순 비교를 위해 'z'로 초기화

# 범위 확인
def is_range(x, y, n, m):
    return 1 <= x <= n and 1 <= y <= m

# DFS
def dfs(n, m, x, y, r, c, k, way, dist):
    global answer
    
    # 현재까지 이동한 거리에 현재 위치에서 목적지까지의 거리의 합이 k보다 커진다면
    # 즉, 현재지점이 목적지에서 멀어지면
    if k < dist + abs(x - r) + abs(y - c):
        return
    
    # 도착지에 도착하고 이동한 거리가 k일 때
    if x == r and y == c and dist == k:
        answer = way
        return
        
    # [하, 좌, 우, 상]으로 이동
    for i in range(4):
        nx, ny = x + dx[i], y + dy[i]
        # 다음 위치가 범위에 속하고 사전순으로 빠를 경우에만 
        if is_range(x, y, n, m) and way < answer:
            dfs(n, m, nx, ny, r, c, k, way + alp[i], dist + 1) # 재귀호출
        
def solution(n, m, x, y, r, c, k):
    total_dist = abs(x - r) + abs(y - c) # 시작점에서 목적지까지의 거리
    
    # 이동해야 하는 거리가 K보다 크면, 이동 불가능
    # K가 더 클 때, K에서 이동해야 하는 거리를 뺐을 때 2의 배수여야 목적지로 돌아올 수 있음
    if total_dist > k or (k - total_dist) % 2 == 1:
        return "impossible"
    
    dfs(n, m, x, y, r, c, k, "", 0)
    
    return answer if answer else "impossible"

풀이

먼저, 처음 접근한 코드는 시간초과로 실패했다.
문제의 키워드를 다시 생각해보고 그림을 그려보았다.

만약, 시작점 - 목적지 거리 가 k 보다 크다면, 절대 이동이 불가능하다.

만약 k 가 더 크다면, k 만큼 이동하기 전에 목적지에 도착할 수가 있다.
이때는 무조건 k 만큼 이동을 해야하므로, 사전 순으로 빠르고 가능한 경로로 이동했다가 다시 목적지로 돌아오면 된다. → Go and Back

이때는, 총 2번 의 과정이 더 필요하게 된다.

즉, k - (시작점 - 목적지 거리) 를 2 로 나눴을 때 0이라면 이동이 가능한 것이고, 아니라면 이동이 불가능한 경우이다.

그래서 total_dist > k or (k - total_dist) % 2 == 1 조건을 추가했다.

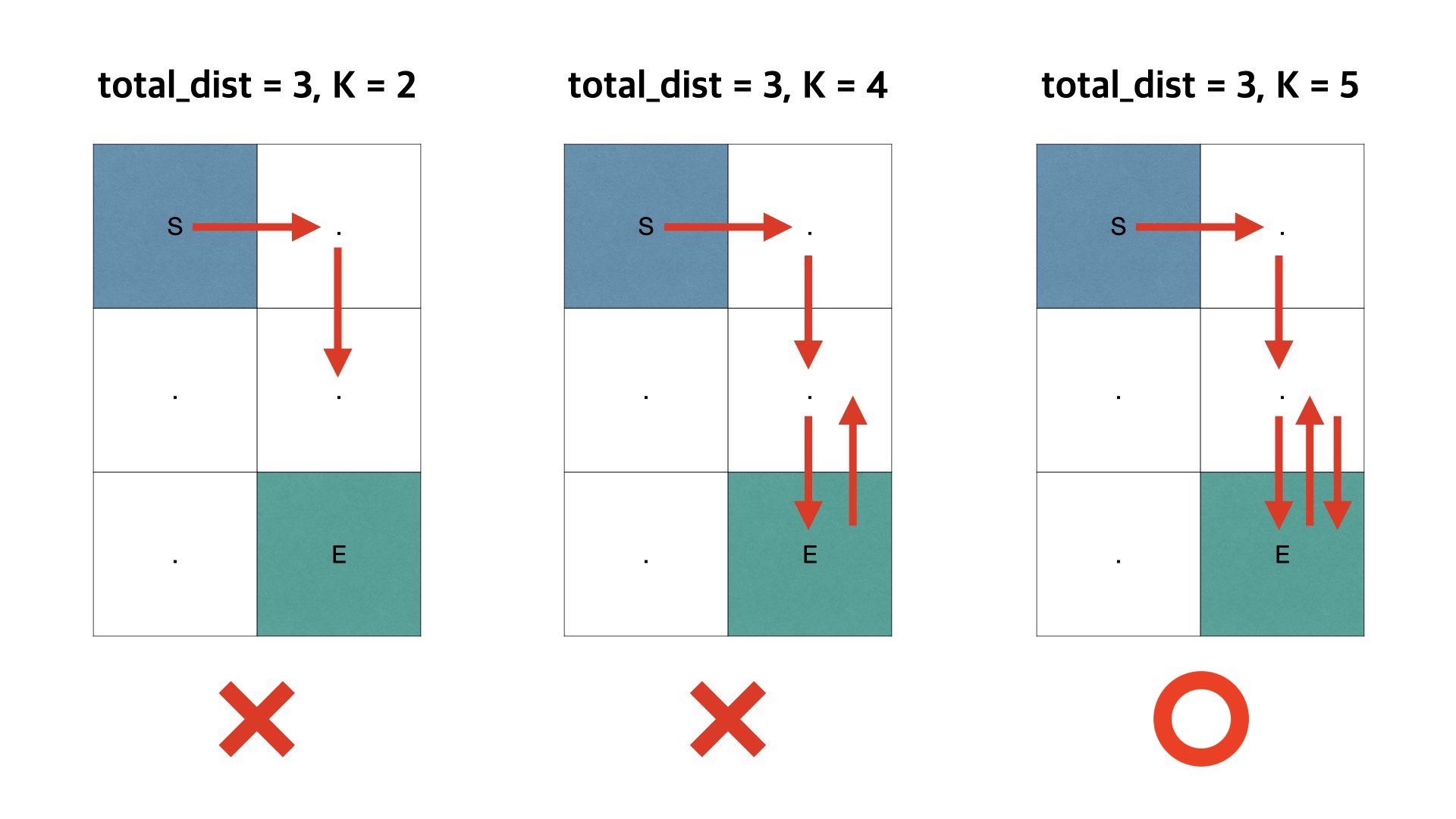
(위 그림의 이동 경로는 하나의 예시일 뿐이다. 다양한 경로가 존재한다.)

DFS 함수 내의 로직을 봤을 때, 처음에는 set에 모든 경로를 저장했는데 파이썬에서 문자열 비교 연산이 안되는 줄 알았는데 '>' , '<' 를 이용한 연산이 가능했다.

이렇게 되면 모든 경로를 저장할 필요없이, 간단하게 풀 수 있다.
먼저 반환할 변수를 answer 라고 가정하고 'z' 로 초기화 해준다.(비교 연산을 하기 위해서)

그리고 방향 이동을 할 때 dfs의 인자로 주어진 way(이동 경로)와 answer를 비교하고
answer보다 사전 순으로 빠를 때 즉, way < answer 일 때 재귀호출을 수행한다.

그러면 항상 answer는 사전 순으로 빠른 경로가 저장이 된다.

처음에는 for문 대신 재귀호출 4번으로 이동 방향을 설정했는데, 이렇게 하면 way와 answer 를 비교하는 if문 을 4번 작성해야하는 번거로움이 생긴다.

위 조건을 모두 추가해줬는데도 시간초과가 발생해서, 다른 사람의 글을 참고했다.

간과한 것이 있었는데 사전 순으로 빠른 경로로 이동을 했다고 하더라도, 이제까지 이동한 거리(dist)와 현재지점에서 목적지까지의 거리(abs(x - r) + abs(y - c))의 합이 k보다 커진다면 문제의 조건과 맞지 않는다.

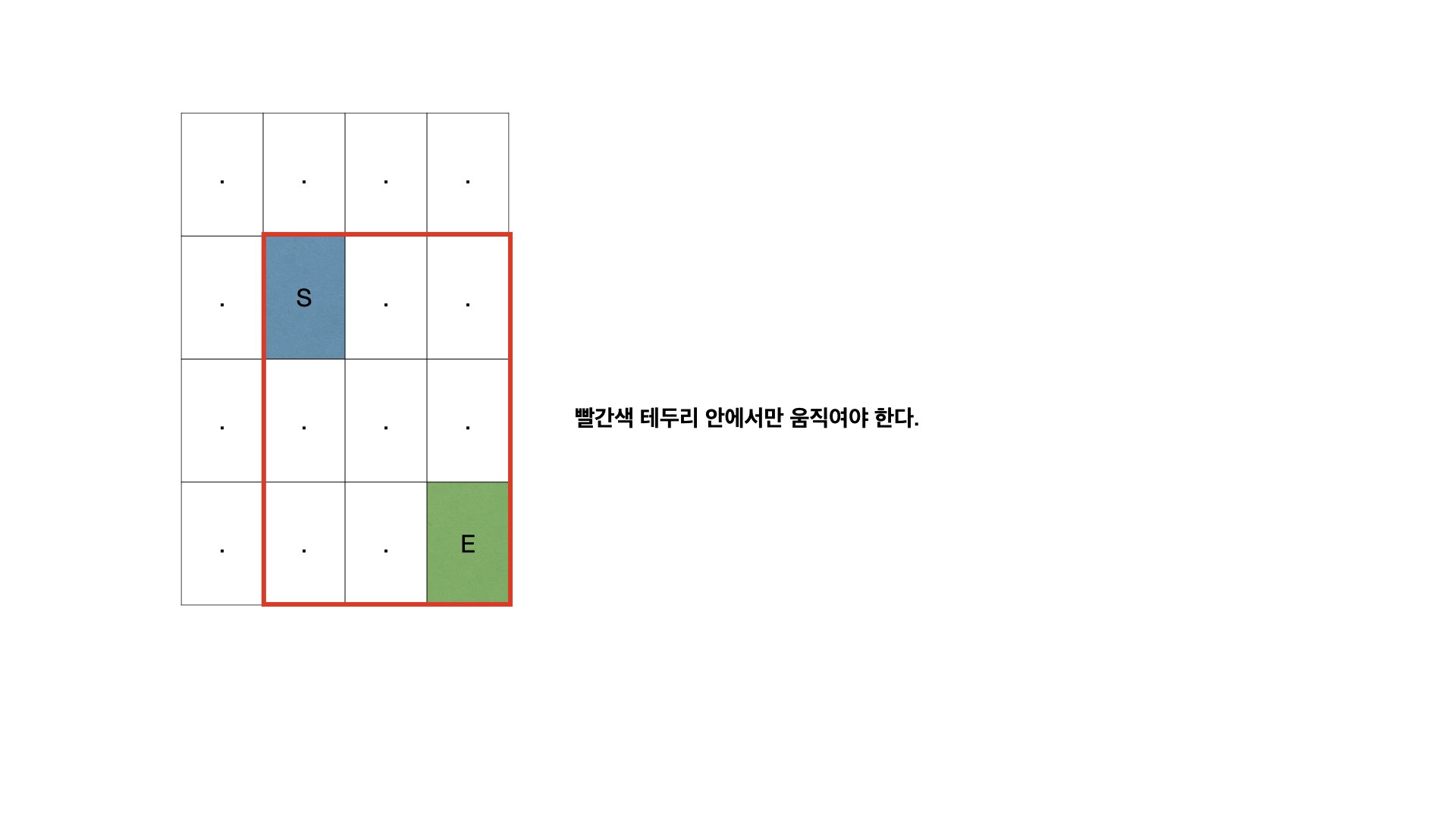
이 부분을 처리하지 못해서 시간초과가 계속 발생했다.

시간복잡도

시간복잡도는 어떻게 되는거지..?

추가 코드

처음에 BFS를 떠올렸을 때 머릿속으로 계산을 때려보니, 조건 처리하기가 어렵다고 생각해서 DFS로 풀었는데 다른 사람의 코드를 참고해서 BFS 코드를 작성해보았다.

코드 - BFS

from collections import deque
import sys
sys.setrecursionlimit(10 ** 6)

dx, dy = [1, 0, 0, -1], [0, -1, 1, 0] # 하, 좌, 우, 상
alp = ["d", "l", "r", "u"]
answer = 'z' # 사전 순 비교를 위해 'z'로 초기화

# 범위 확인
def is_range(x, y, n, m):
    return 1 <= x <= n and 1 <= y <= m

# BFS
def bfs(n, m, x, y, r, c, k, way, dist):
    global answer
    check = [[[0] * (k + 1) for _ in range(m + 1)]  for _ in range(n + 1)]
    q = deque([(x, y, way, dist)])
    check[x][y][0] = 1
    while q:
        x, y, way, dist = q.popleft()
        
        if x == r and y == c and dist == k:
            answer = way
            continue
        
        if k < dist + abs(x - r) + abs(y - c):
            continue
            
        for i in range(4):
            nx, ny = x + dx[i], y + dy[i]
            if is_range(nx, ny, n, m) and way < answer and not check[nx][ny][len(way)]:
                q.append((nx, ny, way + alp[i], dist + 1))
                check[nx][ny][len(way)] = 1
        
def solution(n, m, x, y, r, c, k):
    total_dist = abs(x - r) + abs(y - c) # 시작점에서 목적지까지의 거리
    
    # 이동해야 하는 거리가 K보다 크면, 이동 불가능
    # K가 더 클 때, K에서 이동해야 하는 거리를 뺐을 때 2의 배수여야 목적지로 돌아올 수 있음
    if total_dist > k or (k - total_dist) % 2 == 1:
        return "impossible"
    
    bfs(n, m, x, y, r, c, k, "", 0)
    
    return answer if answer else "impossible"

풀이

코드는 DFS와 거의 유사하지만, 다른 부분이 몇 군데 존재한다.

BFS에서는 방문 처리 배열이 필요하다.
- check로 가정한다면, check[x][y][경로 길이] 는 위치가 (x, y) 일 때 경로의 길이 즉, 같은 길이의 경로로 이미 방문했는지 안했는지 를 판단하는 것이다.
return 이 아닌 continue 를 사용한다.
- DFS 는 재귀호출 방식이라 조건에 맞지 않는다면 return 으로 종료하고, 다음 경우의 수를 살펴본다.
- 하지만, BFS 는 재귀호출 방식이 아니므로 조건에 맞지 않는다면 continue 를 통해 다음 경우의 수를 살펴봐야 한다.

이를 제외하고는 DFS와의 로직은 똑같다.

최악의 경우 약 9000ms 이 소요된다.
그냥 코드도 간단한 DFS로 풀자.

코드 - BFS? 아니면 반복문 사용한 DFS?

from collections import deque
import sys
sys.setrecursionlimit(10 ** 6)

dx, dy = [-1, 0, 0, 1], [0, 1, -1, 0] # 하, 좌, 우, 상
alp = ["u", "r", "l", "d"]
answer = 'z' # 사전 순 비교를 위해 'z'로 초기화

# 범위 확인
def is_range(x, y, n, m):
    return 1 <= x <= n and 1 <= y <= m

def bfs(n, m, x, y, r, c, k, way, dist):
    global answer
    check = [[[0] * (k + 1) for _ in range(m + 1)]  for _ in range(n + 1)]
    q = deque([(x, y, way, dist)])
    check[x][y][0] = 1
    while q:
        x, y, way, dist = q.pop()
        
        if x == r and y == c and dist == k:
            answer = way
            return
        
        if k < dist + abs(x - r) + abs(y - c):
            continue
            
        for i in range(4):
            nx, ny = x + dx[i], y + dy[i]
            if is_range(nx, ny, n, m) and way < answer and not check[nx][ny][len(way)]:
                q.append((nx, ny, way + alp[i], dist + 1))
                check[nx][ny][len(way)] = 1

def solution(n, m, x, y, r, c, k):
    total_dist = abs(x - r) + abs(y - c) # 시작점에서 목적지까지의 거리
    
    # 이동해야 하는 거리가 K보다 크면, 이동 불가능
    # K가 더 클 때, K에서 이동해야 하는 거리를 뺐을 때 2의 배수여야 목적지로 돌아올 수 있음
    if total_dist > k or (k - total_dist) % 2 == 1:
        return "impossible"
    
    # dfs(n, m, x, y, r, c, k, "", 0)
    bfs(n, m, x, y, r, c, k, "", 0)
    
    return answer if answer else "impossible"

풀이

로직은 다음과 같다.

'd', 'l', 'r', 'u' 순서가 아닌, 'u', 'r', 'l', 'd' 순서로 진행한다.
덱에는 다음과 같이 경로가 쌓이게 된다.
- 'u', 'r', 'l', 'd', 'du', 'dr', 'dl', 'dd', ... 'ud'
그리고 덱에서 원소를 뽑아낼 때는 popleft() 가 아닌 pop() 을 사용한다.
- 덱의 끝에는 항상 사전순으로 가장 빠른 경로가 존재하기 때문이다.

최악의 경우 코드 - BFS보다 약 1/9 정도 빠르다.
그래도 DFS 보다는 느리다. DFS 로 풀자.

ZenTechie

데브코스 진행 중.. ~ 2024.03

이전 포스트

[프로그래머스/고득점 Kit] Stack/Queue

다음 포스트