[C++/백준] 1260 DFS와BFS

이 문제를 풀기전에 BFS와 DFS에 대한 개념이 있어야한다.

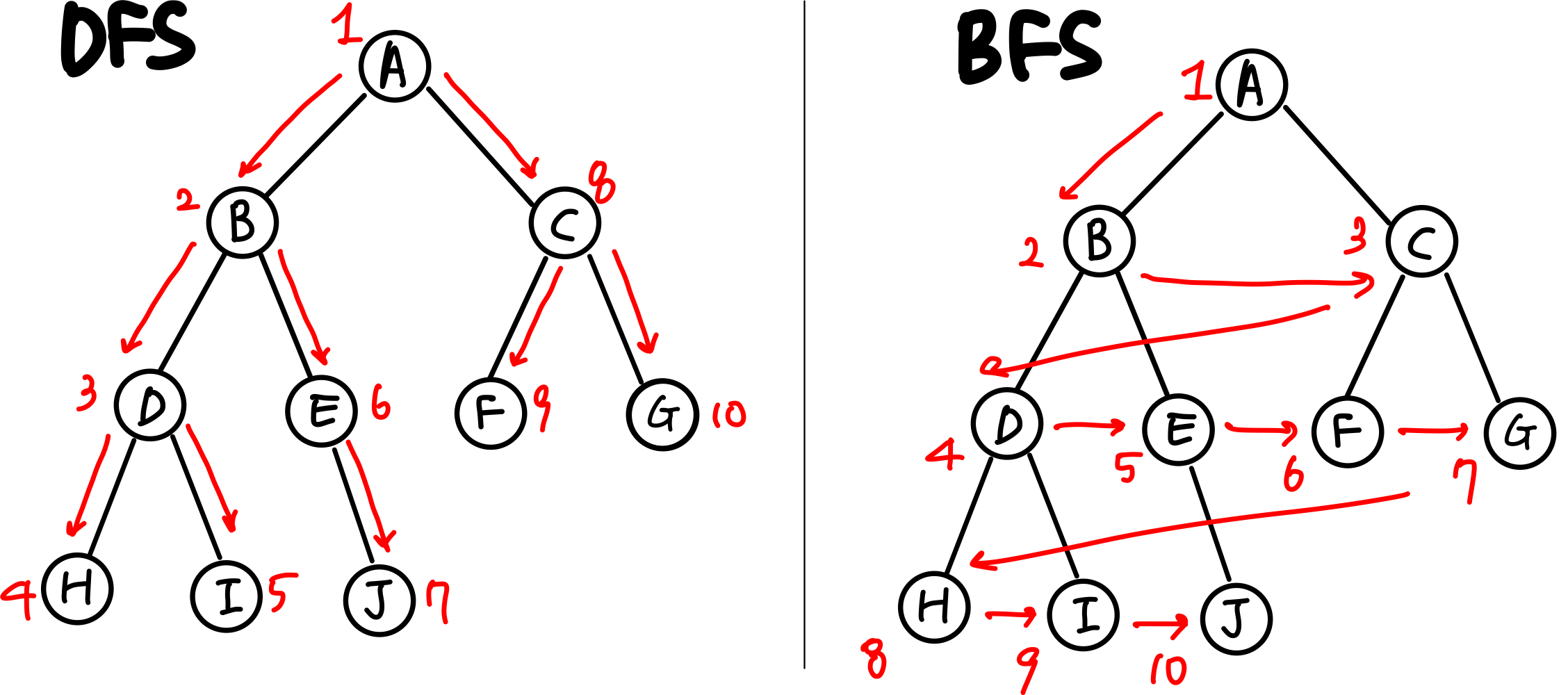
✍BFS(Breath First Search, 넓이 우선 탐색)

:현재 정점에서 갈 수 있는 위치부터 끝까지 탐색해나감. queue로 구현

1. 첫 번째 위치를 큐에 넣는다.
2. 큐에 넣었던 값을 빼낸 후, 그 위치에서 갈 수 있는 경로를 큐에 넣는다
3. 원하는 값을 찾을 때까지 2번을 반복한다.

✍DFS(Depth First Search, 깊이 우선 탐색)

:갈 수 있는만큼 깊게 가고, 더 이상 갈 수 없다면 이전 정점으로 돌아간다. stack으로 구현

1. 첫 번째 위치를 스택에 넣는다.
2. 맨 위에서 하나 빼낸 후, 그 위치에서 갈 수 있는 경로를 스택에 다 넣는다.
3. 원하는 값을 찾을 때까지 2번을 반복한다.

📍둘 다 주의해야할 점!!
이전에 방문했던 위치는 다시 방문하지 않는다.
전에 방문하지 않았고, 값이 있다면 그 다음 위치로 선정될 수 있다

📝문제 포인트

그래프로 탐색해야한다.
그래프는 인접행렬과 인접리스트로 표현할 수 있다.

왼쪽의 그래프를 인접행렬과 인접리스트로 표현해보았다!

인접행렬

: 연결되어있는 위치에 1을 넣어주는 것이다. 0이면 간선이 없어 연결되어있지 않다고 생각하면 된다.

1. 장점 : 구현이 쉽다. 노드간의 연결여부를 알고싶을 때 빠르게 확인할 수 있다.
2. 단점 : 노드를 방문해보고 싶을 때 adj[i][1]부터 adj[i][V]를 모두 확인해보아야 하기 때문에 비효율적이다.

ex)graph[0][1]=1 / graph[1][3]=0

인접리스트

: 각 정점에 인접한 정점들을 리스트로 표현하는 방법이다.
c++의 경우 vector 컨테이너를 이용하면 된다!

1. 장점 : 실제로 연결되어 있는 노드의 정보만 담기 때문에 메모리를 적게 차지한다. 모든 노드를 다 방문하는 경우 시간적 이점이 존재한다.
2. 단점 : 노드간의 연결여부를 알기 위해서는 노드를 다 탐색해야 한다

   ---

✍코드

사족이 길었지만 코드는 인접행렬로 구현했다는 이야기였다 ..(⊙_⊙;)

#include <iostream>
#include <queue>
#include <cstring>
#define MAX 1001
using namespace std;

int n, m, v;
int a, b;
int map[MAX][MAX];
bool visited[MAX];
queue<int>q;

void bfs(int v) {
	visited[v] = 1;
	q.push(v);

	while (!q.empty()) {
		v = q.front();
		q.pop();
		cout << v << " ";
		for (int i = 1; i <= n; i++) {
			if (map[v][i]  && !visited[i]) {
				q.push(i);
				visited[i] = 1;
			}
		}
	}
}

void dfs(int v) {
	cout << v << " ";
	visited[v] = 1;
	for (int i = 1; i <= n; i++) {
		if (map[v][i]  && !visited[i]) {
			dfs(i);
		}
	}
}

int main() {
	ios_base::sync_with_stdio(0);
	cin.tie(0); cout.tie(0);

	cin >> n >> m >> v;
	for (int i = 0; i < m; i++) {
		cin >> a >> b;
		map[a][b] = map[b][a] = 1;
	}
	dfs(v);
	cout << '\n';
	memset(visited, false, sizeof(visited));
	bfs(v);
	cout << '\n';
}