움직이는 소수점에 대해서 알아?

55555-Jyeon·2024년 9월 8일

Deep Dive

목록 보기

8/8

부동소수점에 대해 글을 쓰는 이유

최근 면접을 보게 되었는데, 부동소수점으로 인한 오류에 대해 알고 있는지 질문을 받게 되었습니다. 오류가 발생한다는 사실만 기억이 나고 이유가 전혀 기억이 안 나더라구요. 그래서 다시 한 번 정리를 할 겸, 궁금하기도 해서 겸사 겸사 글로 남겨 봅니다 :)

움직이는 소수점?

프로그래밍 언어에서는 소수가 있는 수를 표현하기 위해 부동소수점이라는 것을 사용합니다.
여기서 부동은 뜰 부(浮), 움직일 동(動)을 사용해 "떠서 움직이는" 이라는 의미를 갖고 있어요. 영어로는 floating point라고도 합니다.

소수점이 움직이기 때문에 어떤 오류가 발생한다는 사실을 알고 계신가요?

🤔 어? 무슨 오류가 발생하는데...?

0.1 + 0.2 = ?

위의 식을 프로그래밍 언어로 출력하면 어떤 결과값이 나올 것 같나요?

0.3이라고 생각하셨나요?
음... 컴퓨터는 다르게 생각할 것 같습니다.

엥, 무슨 소리냐고요?

프로그래밍 언어로 0.1+0.2가 0.3인지 확인해보면 false라고 출력하기 때문입니다.

// javascript

console.log(0.1) // 0.1
console.log(0.2) // 0.2
console.log(0.1 + 0.2 === 0.3) // false

뭐야, 왜 이래?

이건 비단 자바스크립트만의 문제는 아닙니다.
어떤 언어로 작성하든 프로그래밍 언어라면 모두 false가 찍히게 되거든요.

// java

public class App {
	System.out.println(0.1 + 0.2 === 0.3) // false
}

// python

print(0.1 + 0.2 === 0.3) // false

🤯 프로그래밍 언어가 이래도 돼?

0.1 + 0.2 !== 0.3

0.1과 0.2를 더한 값이 0.3이 아닌 이유는 0.1과 0.2가 0.1, 0.2가 아니기 때문입니다.

console.log(0.3) // 0.3
console.log(0.1 + 0.2) // 0.300..04

콘솔에 각각 찍어보면 0.1과 0.2를 더한 값이 0.3보다 조금 큰 것을 확인할 수 있습니다.
여기서 발생한 0.000...4가 부동소수점 때문에 생기는 오차입니다.

이 오차 때문에 0.1+0.2 === 0.3이 false로 나오게 됩니다.

프로그래밍 언어에서는 소수가 있는 수를 표현하기 위해 움직이는 소수점을 사용합니다.
즉, 소수점이 움직이기 때문에 오차가 발생한다는 거죠.

왜 떠다니는 건데?

소수점이 움직이기 때문에 오류가 발생한다면 그냥 고정시키면 안 되는 걸까요?
왜 굳이 오류를 발생시키게 소수점을 움직이게 하는 걸까요?

컴퓨터는 메모리를 가장 효율적으로 활용할 수 있는 방법으로 데이터를 저장합니다.
즉, 부동소수점이 메모리를 효율적으로 관리할 수 있는데 가장 효과적이라는 의미가 되겠죠?
왜 부동소수점을 사용하는 것이 오차가 있음에도 가장 효율적인지 알아보기 위해 먼저 프로그래밍 언어에서 자주 사용되는 숫자와 관련된 자료형에 대해서 간단히 알아보겠습니다.

정수를 위한 integer(int)

자바스크립트에는 없지만, 자바와 파이썬, c# 등에서 사용하는 int는 소수점이 없는 정수 데이터를 저장하는데 사용되는 자료형입니다.

int는 32개의 비트를 사용해 정수를 표현합니다.

그 중 첫 번째 자리에는 정수와 음수를 구분짓는 부호가 들어가게 됩니다.
0이 들어가면 양수, 1이 들어가면 음수가 됩니다.
그리고 나머지 31개의 비트로 절대값을 표현합니다.

양수는 0부터 2,147,483,647까지 나타낼 수 있습니다.

음수로는 -1부터 -2,147,483,648까지 나타낼 수 있죠.

따라서 int 자료형으로 표현 가능한 정수의 범위는 -2,147,483,648부터 2,147,483,647입니다.

엄밀히 말하면 수학적 개념의 실수는 아니지만 아무튼

실수를 위한 number와 float

자바와 파이썬에서 사용하는 float와 자바스크립트에서 사용하는 number 자료형으로는 실수를 표현하는데 사용되며 부동소수점(floating-point) 자료형이라고도 합니다.

125.925와 같은 실수를 아래와 같이 32비트로 표현하고자 한다고 가정해봅시다.
정수부와 소수부를 어떻게 나눌 수 있을까요?

고정소수점

이때 int와 마찬가지로 양수와 음수를 구분하는 첫 번째 자리를 제외한 나머지 31개의 비트를 대략 반으로 나눠 15비트는 정수부를, 16비트는 소수부를 표현하는데 사용하는 것을 고정소수점이라고 합니다.

고정소수점은 소수점의 위치가 고정된 형태로, 메모리 내에서 소수 부분과 정수 부분이 명확히 구분되어 있습니다. 이 방식은 정확도를 유지할 수 있지만, 표현할 수 있는 수의 범위가 제한적이라는 큰 단점이 있습니다.

소수점의 위치를 고정해버리면 위치가 어디든 수의 범위가 제한적일 수 밖에 없기 때문에 컴퓨터는 부동소수점을 사용하는 것입니다.

부동소수점

부동소수점, 이름의 의미

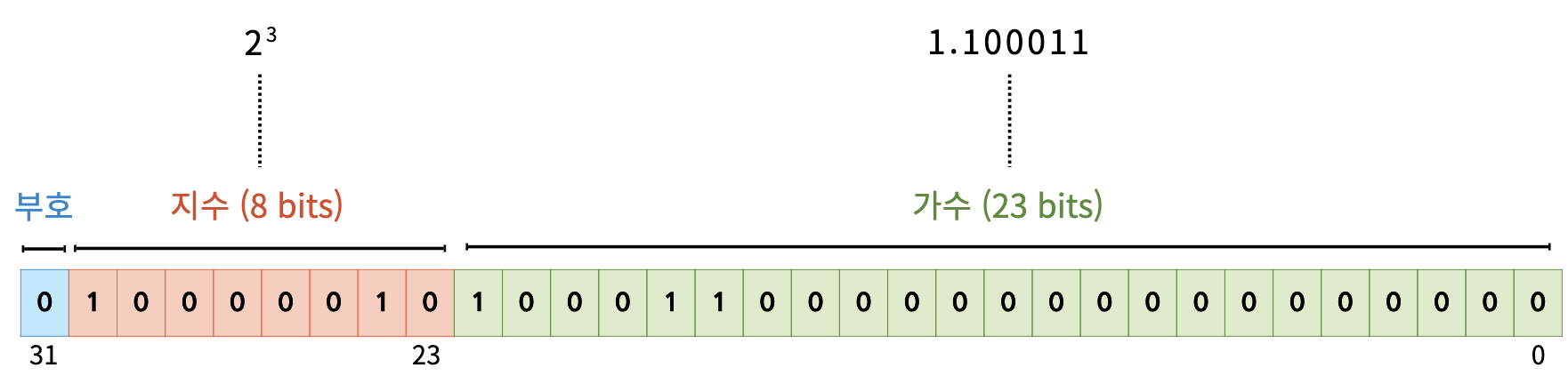
마찬가지로 첫 번째 자리를 양수와 음수를 나누는데 사용합니다.
그리고 부동소수점은 이진수 숫자를 항상1.xxxxx 형식으로 변환하기 때문에 이진수로 변환한 값에서 소수점이 몇 칸 이동해야 될지를 다음 8비트로 나타냅니다.
나머지 23비트엔 소수점이 움직인 결과에서 소수점 뒤로 오는 부분들을 채워넣습니다.

이진수를 특정 형식으로 변환하는 과정을 정규화라고 하는데, 이 과정 때문에 부동소수점이라는 이름이 붙었습니다.

예시로 더 자세히 👀

예를 들어, 십진수 9.625를 컴퓨터가 저장한다고 가정해보겠습니다.

① 10진수를 2진수로 변환

먼저 10진수를 2진수로 변환할 때에는 정수부와 소수부를 나눠 변환합니다.
정수부는 몫이 0이 될 때까지 2로 나누고, 소수부는 소수부가 0이 될 때까 2를 곱합니다.

위 예시에서 9.625를 2진수로 변환하면 정수부인 9는 1001, 소수부 0.625는 0.101이 됩니다.
따라서 9.625는 1001.101이 됩니다.

② 정규화(normalization)

부동소수점은 항상 1.xxxxx 형식으로 숫자를 표현합니다.

따라서 위에서 변환된 이진수1001.101을 1.001101로 변환합니다.

③ 지수(exponent)를 구하기

지수는 정규화 과정에서 소수점이 몇 칸 이동했는지를 나타내는 부분입니다.

소수점을 세 칸 왼쪽으로 이동했으므로, 지수는 3입니다.
그러나 IEEE 754 형식에서는 바이어스(bias)를 더해 지수를 저장합니다.

32비트 부동소수점의 바이어스는 127입니다.
따라서, 실제 지수는 3 + 127 = 130이 됩니다.

130을 이진수로 표현하면 10000010입니다.

💡 IEEE 754

IEEE 754는 컴퓨터에서 부동소수점(floating-point) 수를 표현하고 연산하는 표준을 정의한 규격입니다.
이 표준은 부동소수점을 일관성 있고 효율적으로 처리하기 위해 제정되었으며, 대부분의 프로그래밍 언어와 하드웨어에서 사용됩니다.

💡 바이어스가 왜 127인가요?

바이어스(bias)는 지수를 저장할 때 기준이 되는 값입니다.
지수에 바이어스를 더해 양의 정수 형태로 저장되며 바이어스는 지수부의 비트 수에 따라 결정됩니다.

단정밀도(32비트) : 지수부가 8비트, 바이어스 값은 127 ( $2^{7} - 1 = 127$ )

배정밀도(64비트) : 지수부가 11비트,바이어스 값은 1023 ( $2^{10} - 1 = 1023$ )

④ 가수(significand, mantissa)

정규화 과정에서 변환된 1.001101에서 소수점 뒤의 숫자들(001101)이 가수 부분이 됩니다.
가수는 23비트로 표현되며, 남는 부분은 0으로 채워집니다.

즉, 위의 예시의 경우 00110100000000000000000이 가수 부분이 됩니다.

⑤ 부호(sign)

부호는 위에서도 설명한대로 양수면 0, 음수면 1이 표시됩니다.

예시의 숫자는 양수이므로 부호 비트는 0입니다.

⑥ 최종 부동소수점 표현

부호 비트(1비트) + 지수(8비트) + 가수(23비트)를 결합해 32비트 부동소수점으로 표현한 값이 완성됩니다.

예를 들어, 위 9.625의 경우는 아래와 같습니다 :

0 | 10000010 | 00110100000000000000000

부동소수점은 소수점의 위치가 고정되지 않기 때문에 고정소수점보다 더 넓은 수의 범위를 표현할 수 있습니다. 특히, 자바스크립트에서 숫자는 모두 부동소수점으로 처리됩니다.
하지만 이로 인해 위에서 대략적으로 알아본 것 같이 오차가 발생할 수 있죠.
오차 발생으로 인한 오류는 부동소수점 계산의 대표적인 한계라고 볼 수 있습니다.

오류가 왜 생기는 건데?

오류는 2진수로 소수를 표현할 때 발생합니다.
십진수에서는 0.1 같은 값이 익숙하지만, 이진수에서는 이 값이 정확히 표현되지 않기 때문에 컴퓨터는 근사치로 계산하게 됩니다.

숫자라는 추상적인 개념을 표현하기 위해 사람은 십진수를, 컴퓨터는 이진수를 사용합니다.
그리고 이 간극에서 발생하는 차이로 인해 오류가 발생하게 됩니다.

Decimal, 십진소수점수

십진수는 소수점을 기준으로 위의 수는 10을 곱한, 아래 수들을 10으로 나눈 개념입니다.
0.1을 10개 가져다 놓으면 1.0이 되죠.
이렇게 사람은 자연스럽게 소수점 아래 부분도 십진법으로 계산하고 있습니다.

유한십진소수점수는 10으로 나누다보면 언젠가 나누어 떨어지는 지점이 존재합니다.
반대로 무한십진소수점수는 아무리 10으로 나누어도 근사값에 접근할 뿐 나누어 떨어지지 않습니다.

예를 들어, 1/3을 십진수로 나타내면 무한십진소수점수가 됩니다.

Binary, 이진소수점수

반대로 컴퓨터는 이진소수점수로 숫자를 표현합니다.
2를 기준으로 설명하기 때문에 위와 같은 예를 이어가자면 0.1을 2개 가져다 놓으면 1.0이 되는 겁니다.

따라서 이진소수점수 0.1은 십진소수점수의 0.5와 같습니다.

❗️ 수학적인 개념으로 접근하지 말아주세요

이진소수점수도 십진소수점수와 마찬가지로 유한소수점수와 무한소수점수가 존재합니다.
유한이진소수점수는 2로 나누다보면 언젠가 나누어 떨어지는 지점이 존재하고 이진무한소수점수는 2로 나누어 떨어지는 지점이 존재하지 않습니다.

대표적인 무한이진소수점수는 맨 처음 예시로도 등장했던 0.1입니다.

컴퓨터는 유한한 메모리로 인해 무한이진소수점수를 저장할 수 없습니다.
그래서 위에서 알아본 것처럼 32비트의 저장공간 안에 이 무한한 수를 욱여넣습니다.

우겨넣는 과정에서 32비트 이하 자리수는 반올림 후 버리게 됩니다.
여기서 버려지고 반올림되는 과정에서 숫자 계산에서 미세한 오차가 생기게 되고 위와 같이 0.1과 0.2를 더한 값이 0.3이 아니라는 결과를 반환합니다.

0.1과 0.2를 더한 값과 0.3의 차이는 굉장히 미세하지만 이런 미세한 오차들이 누적되면 큰 차이가 발생하게 됩니다.
이진수로 정확히 표현할 수 없는 수들은 근사치로 밖에 표현이 안 되기 때문에 근차시 연산의 오류가 발생하게 되는 것입니다.

그럼 왜 이렇게까지 하는 건데?

오차 발생이라는 한계가 있음에도 왜 컴퓨터는 부동소수점을 사용할까요?

위에서도 언급했지만 컴퓨터는 메모리를 가장 효율적으로 활용할 수 있는 방법으로 데이터를 저장합니다. 한정된 메모리 공간에서 좀 더 넓은 범위의 소수를 표현하기 위해 부동소수점을 사용합니다.

그냥 정수로 하지, 왜?

기본적으로 컴퓨터의 소수점수(floating-point)는 아주 큰 수나 아주 작은 수를 효율적인 리소스를 토대로 연산하기 위해서 지원되기 시작했습니다.

CPU는 연산을 할 때 ALU(Arithmetic Logic Unit)에서 처리합니다.
하지만 소수점수는 ALU에 포함되어 있는 FPU(Floating Point Unit)에서 처리하게 됩니다.

십진연산은 하드웨어적인 측면에서 봤을 때에도 비효율적이며 소프트웨어로도 가능하기 때문에 컴퓨터는 이진연산을 합니다.

그래서 항상 소수점수에는 정밀도 문제가 꼬리표처럼 따라다닐 수 밖에 없고, 컴퓨터는 소수점수의 값을 대부분 근사치로 계산해 표현합니다.

그럼 어떻게 해결해?

부동소수점 오류는 몇 가지 방법으로 해결하거나 최소화할 수 있습니다.
아래에서 가장 자주 사용되는 몇 가지 해결책을 정리해보겠습니다.

1️⃣ 반올림하여 처리하기

프로그래밍 언어에서 제공하는 반올림 함수로 부동소수점 연산의 미세한 오차를 줄일 수 있습니다.
자바스크립트에서는 toFixed() 또는 Math.round() 같은 함수를 이용할 수 있습니다.

// javascript example
console.log((0.1 + 0.2).toFixed(1)); // 0.3
console.log(Math.round(0.1 + 0.2)); // 0

위와 같이 원하는 자릿수에서 반올림함으로써 오차를 줄일 수 있습니다.
하지만, 이 방법은 근본적으로 오류를 없애는 게 아니라 오차를 무시하는 것이기 때문에 아주 큰 수나 작은 수에서는 문제가 될 수 있습니다.

2️⃣ 정수로 변환하여 처리하기

소수점 연산에서 발생하는 오차를 피하기 위해, 정수 단위로 변환 후 연산을 하고 나중에 다시 소수점으로 되돌리는 방법도 많이 사용됩니다.
이 방법은 특히 금융 분야에서 자주 사용되며, 정밀도가 중요한 계산에 적합합니다.

// javascript example: 금액 계산
let price1 = 100; // 1.00 달러를 센트로 표현
let price2 = 200; // 2.00 달러를 센트로 표현
let total = price1 + price2; // 300 센트
console.log(total / 100); // 3.00 달러

예를 들어, 금액 계산 같은 경우 소수점을 피하기 위해 센트 단위로 변환한 후 계산할 수 있습니다.

3️⃣ `Number.EPSILON` 사용하여 비교하기

자바스크립트에서는 부동소수점의 오차를 고려하여 두 숫자가 거의 같은지를 판단할 수 있는 허용 오차를 지정해 비교하는 방법이 있습니다.
Number.EPSILON은 부동소수점 비교 시 아주 작은 차이를 무시할 수 있도록 도와줍니다.

// 자바스크립트 예시: Number.EPSILON을 이용한 비교
function areEqual(a, b) {
  return Math.abs(a - b) < Number.EPSILON;
}

console.log(areEqual(0.1 + 0.2, 0.3)); // true

4️⃣ 고정소수점 라이브러리 사용하기

부동소수점의 오차 문제를 근본적으로 해결하기 위해 고정소수점 연산을 지원하는 라이브러리를 사용할 수 있습니다.

예를 들어, 자바에서는 BigDecimal 클래스를 사용해 더 정확한 실수 연산을 할 수 있습니다.

이 방법은 정밀한 계산이 중요한 금융 및 과학 분야에서 많이 사용되며, 부동소수점 연산의 오류를 완전히 없앨 수 있습니다.

자바스크립트에서 사용 가능한 라이브러리

① Big.js

작은 크기와 빠른 속도를 자랑하는 고정소수점 연산 라이브러리입니다.
부동소수점 연산에서 발생하는 오류 없이 정확한 실수 연산을 수행할 수 있습니다.

import Big from 'big.js';

let a = new Big(0.1);
let b = new Big(0.2);

console.log(a.plus(b).toString()); // 0.3

② Decimal.js

자바스크립트에서 매우 높은 정밀도로 소수점 연산을 수행할 수 있는 라이브러리입니다.
수백 자리의 정밀도를 제공하며, 부동소수점의 오차 문제를 완전히 해결할 수 있습니다.

import Decimal from 'decimal.js';

let a = new Decimal(0.1);
let b = new Decimal(0.2);

console.log(a.plus(b).toString()); // 0.3

③ BigNumber.js

수천 자리 이상의 정밀도를 지원하며, 부동소수점 연산에서 정확성을 보장하는 라이브러리입니다.
암호화폐 계산이나 금융 계산과 같이 높은 정밀도가 요구되는 경우에 적합합니다.

import BigNumber from 'bignumber.js';

let a = new BigNumber(0.1);
let b = new BigNumber(0.2);

console.log(a.plus(b).toString()); // 0.3

④ math.js

수학 계산을 위한 강력한 라이브러리로, 고정소수점 연산, 행렬 계산, 통계 등 다양한 수학적 기능을 제공합니다.
고정소수점 연산에서도 사용 가능하며, 복잡한 계산에 적합합니다.

import { bignumber, add } from 'mathjs';

let a = bignumber(0.1);
let b = bignumber(0.2);

console.log(add(a, b).toString()); // 0.3

5️⃣ 다중 정밀도 라이브러리 사용하기

부동소수점 문제를 해결하기 위해 decimal.js 같은 다중 정밀도 라이브러리를 사용하면 소수점 연산의 정밀도를 높일 수 있습니다.
이 방법은 계산의 정확성을 극대화하지만, 성능상의 비용이 발생할 수 있습니다.

이 방법은 매우 정밀한 계산이 필요한 경우에 유용하며, 자바스크립트뿐만 아니라 다양한 언어에서 사용할 수 있는 라이브러리들이 존재합니다.

References.

[👩🏻‍💻 Blogs]

[🎥 Videos]

55555-Jyeon

🥞 Stack of Thoughts

이전 포스트