🤔 Synchronous algorithm의 한계
앞선 포스트에서 설명했던 Bellman-Ford, Dijkstra, FloydWell의 경우 Synchronous algorithm에 해당한다. 그러나, 이런 Synchronous algorithm에도 단점이 존재한다.
- Shortest Path를 구성하는 라우터들 중 하나가 꺼져있다면? 이 상황에 Synchronous Algorithm을 구동한다면 진짜 Shortest Path가 아니라 다른 Path가 구성되기 때문에 모든 라우터들이 동시에 Power On 되어야 한다.
-> 모든 라우터들이 동시에 Power On 되어야 한다. - Algorithm이 동작하는 시간 동안에 도중에 라우터가 꺼지거나 link가 끊어지거나 하는 이유 등으로 Cost가 바뀐다면, 처음부터 다시 Algorithm을 시작해야 한다. Algorithm을 돌리면서 지금까지 했던 Step들이 무용지물이 되기 때문이다.
-> Link나 Topology에 변화가 있다면 지금 하고 있던 것을 멈추고 다시 알고리즘을 구동시켜야 한다.
이런 문제를 해결하기 위해 나온 것이 바로 Distributed Asynchronous Bellman-Ford Algorithm이라고 한다.
- Distributed : 라우터들이 각자 알고리즘을 구동한다.
- Asynchronous : 동시에 라우터들이 켜지지 않아도 된다.
이 알고리즘은 Distance Vector Routing Algorithm 라는 말로 더 자주 불린다.
😁 Distributed Asynchronous Bellman-Ford Algorithm
역시 이 알고리즘 역시도 Bellman-Ford 알고리즘을 사용한다. 이 말은 곧 Bellman's equation을 사용한다는 것이다.
Bellman's Equation은 앞선 포스트에서도 다루었지만 다시 한번 다뤄보자면, 인접 노드들이 자신과 목적지 노드까지의 거리를 소스 노드에게 알려주는데, 이 정보를 소스 노드는 받아 인접 노드와의 거리를 더해 가장 작은 거리값을 가지는 노드를 Shortest Path로 설정하는 것이다.
이 Bellman's equation을 기본으로 하되, Asynchronous 적으로 동작해야 하기 때문에 인접 노드들이 주기적으로 거리 정보들을 보내주고, 이 정보를 받아서 계속해서 라우팅 테이블을 업데이트 해나가는 방식이다. 이를 그림으로 살펴보자.
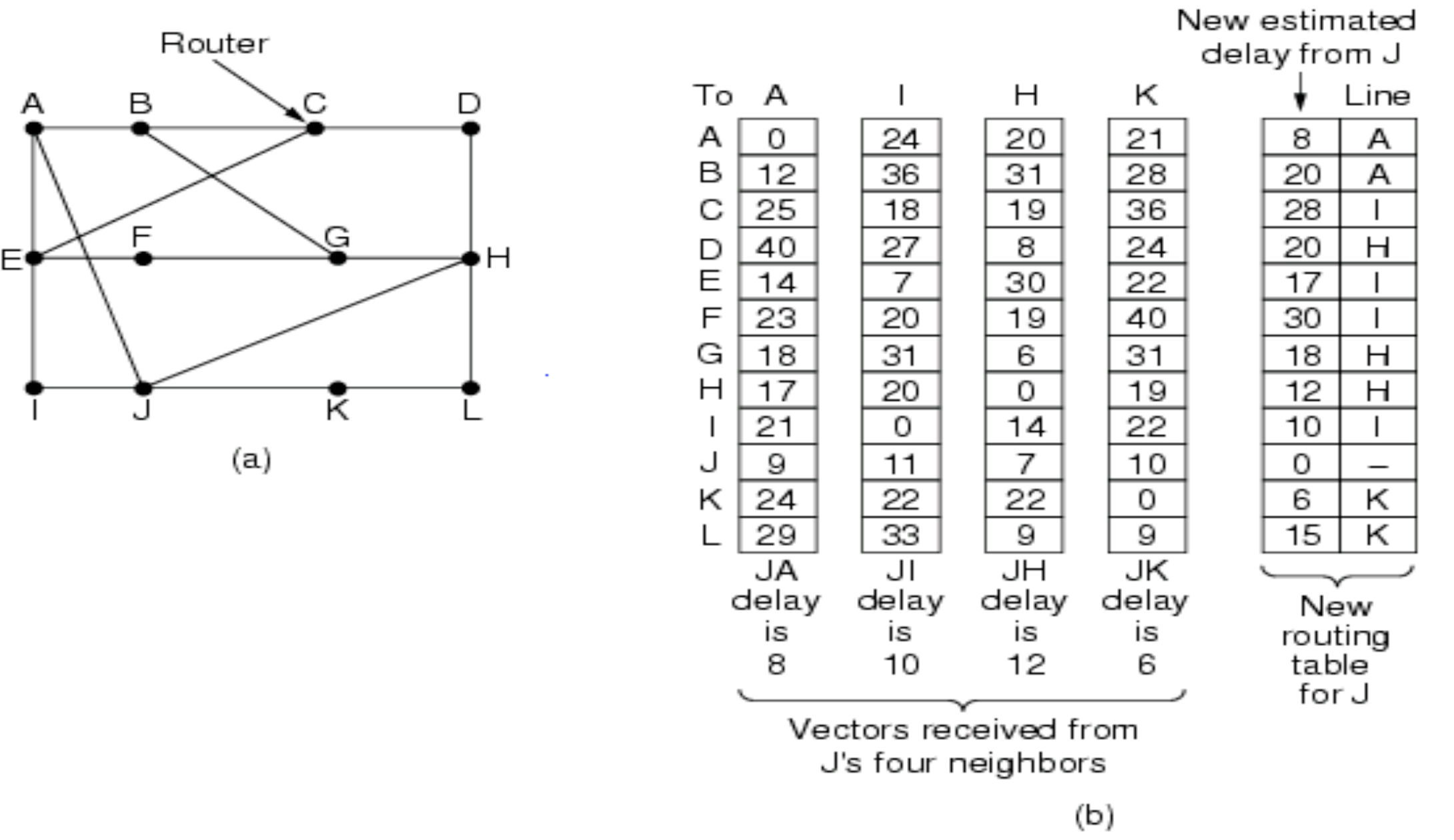
다음 그림은 J가 Source Node일 때, 인접 노드들인 A, I, H, K들에서 J에게 보내주는 정보들과 이걸 토대로 J가 업데이트한 라우팅 테이블이다.
각 인접 노드들에서 보내준 거리 정보들과 소스에서 인접 노드까지의 각 거리를 더한 값 중 가장 작은 값을 선택하여 라우팅 테이블로 만드는 것이다. 이렇게 되면 J는 각 노드들로 보낼 수 있는 거리값을 알 수 있고, 목적지 노드로 보내려면 어느 인접 노드로 보내야 할 지 판단할 수 있게 된다.
그림에서도 J가 C로 가기 위해 Shortest Path를 선택하는 과정을 알 수 있다. 인접 노드들 A, I, H, K로부터 받은 C까지의 거리는 각각 25, 18, 19, 36이고, 여기에 J에서 인접 노드들까지의 거리를 더하면 총 33, 28, 31, 42가 된다. 28이 제일 작은 거리이므로 J는 I로 보내면 28이라는 가장 작은 비용으로 C까지 도달할 수 있겠다!라는 것을 알게 되고, 자신의 라우팅 테이블을 (28,I)로 업데이트한다.
