벨만-포드 알고리즘

• 그래프 최단 경로를 구하는 알고리즘
• 하나의 정점에서 출발하는 최단 거리를 구함. (출발지만 정함.)
• 음수 사이클 없어야 함.
• O(nm) 시간 복잡도
• 동적 계획법 사용, relaxation 기법

vs Dijkstra

벨만 포드의 경우는 음수 가중치가 존재하는 경우에도 적용할 수 있지만 다익스트라는 음수 간선 자체가 존재할 수 없음.
대신 다익스트라는 벨만 포드에 비해 실행 속도가 빠름. (O(VlongV) V: 정점 개수)

음수 가중치의 문제

음의 가중치 자체가 문제가 되는 것은 아니지만, 음의 값이 누적되는 사이클을 형성하면 문제가 됨.

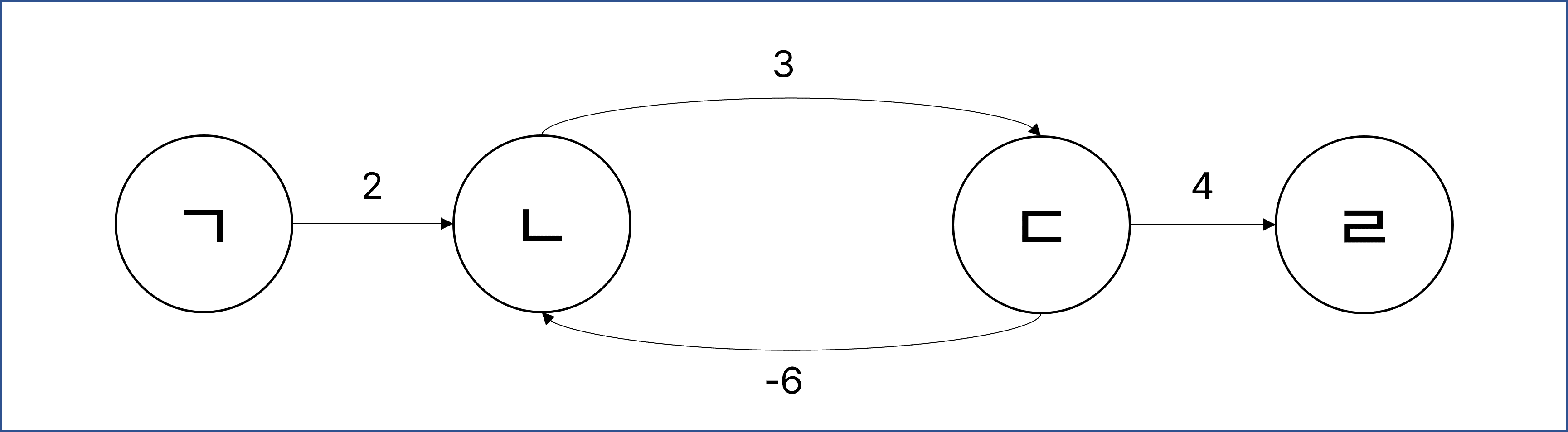
예를 들어서 노드 ㄱ에서 노드 ㄹ까지의 최단 거리를 구한다고 할 때, 2 → 3 → -6 → 3 → -6 → …의 음의 값이 누적되는 사이클이 형성되며, 이 사이클을 무한히 돌아야 최단 거리가 반환됨.

벨만-포드 알고리즘 동작 과정

각 정점들을 차례로 돌아가면서 해당 정점의 간선들을 탐색함.
단, 맨 처음은 시작점부터 탐색함.
그리고 그 간선의 가중치와 시작점에서 정점까지의 거리의 합이 해당 간선이 도달하고자 하는 정점의 기존 거리보다 작으면 업데이트 함.

d[T] ≤ d[S] + w(S, T)

d - 시작점에서 해당 정점의 거리
w - 해당 간선의 가중치
T - 해당 간선이 도달하고자 하는 정점
S - 해당 간선의 시작점

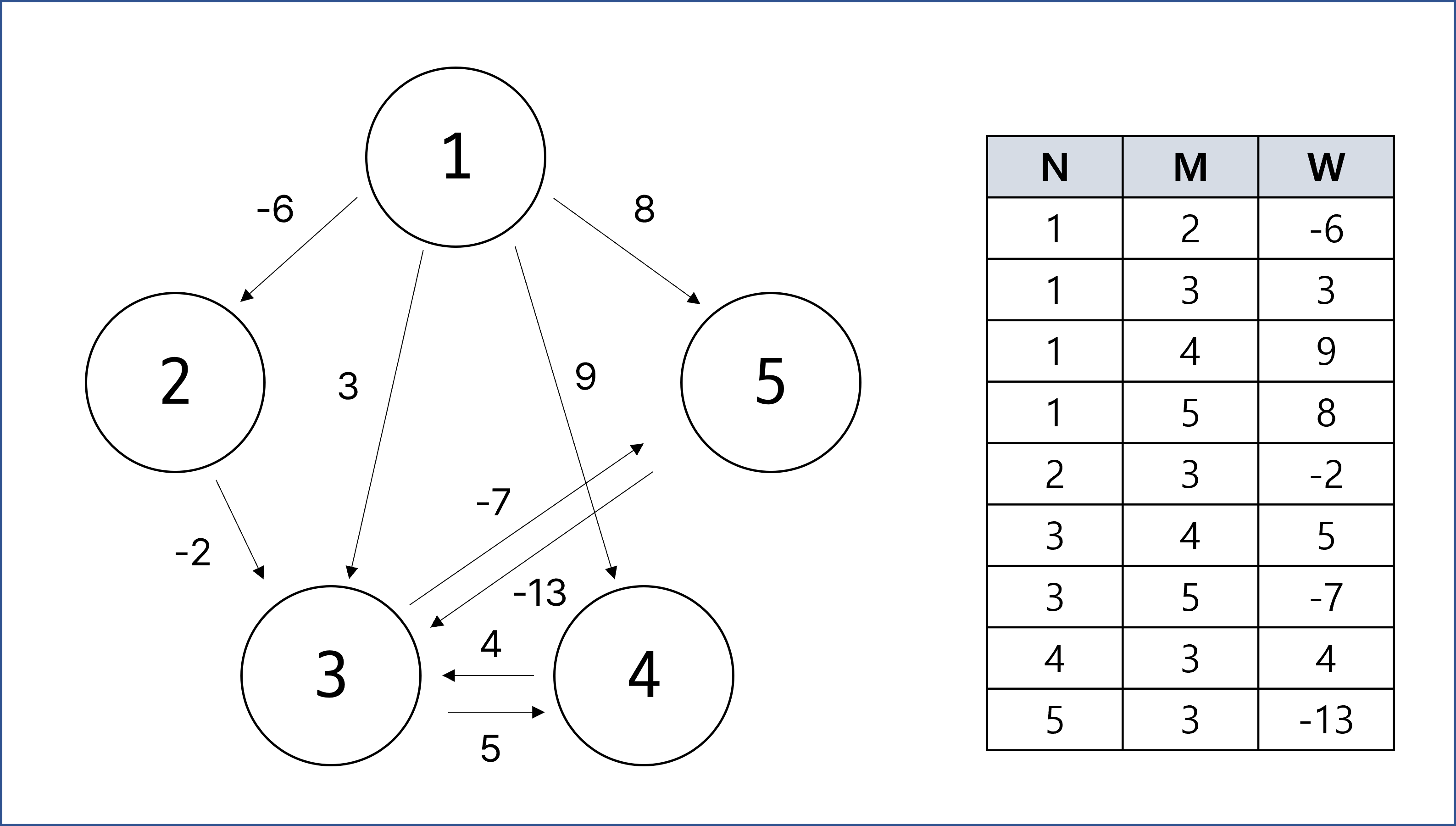
예를 들어서 다음과 같은 노드 5개와 간선 9개가 있다고 하자.

[1번 노드]

1번 노드는 모든 노드와 연결되어 있기 때문에 가중치를 갱신함.

0	-6	3	9	8

[2번 노드]

2번 노드는 3번 노드와 연결되어 있으며, 1→3의 3보다 1→2→3의 -8이 더 작으므로 가중치를 갱신함.

0	-6	-8	9	8

[3번 노드]

3번 노드는 4번 노드와 5번 노드와 연결되어 있음.
1→4의 9보다 1→2→3→4의 -3이 더 작으므로 가중치를 갱신하며,
1→5의 8보다 1→2→3→5의 -15가 더 작으므로 가중치를 마저 갱신함.

0	-6	-8	-3	-15

[4번 노드]

4번 노드는 3번 노드와 연결되어 있음.
1→4→3의 5가 -8보다 크므로 갱신하지 않음.

0	-6	-8	9	8

[5번 노드]

5번 노드는 3번 노드와 연결되어 있음.
1→5→3의 -5가 -8보다 크므로 갱신하지 않음.

0	-6	-8	9	8

다음과 같은 과정을 노드 개수 - 1번 반복해야 함.

그리고 추가적으로 음의 사이클의 존재 여부를 파악하고 싶다면 마지막으로 한 번 더 반복하여 총 노드 개수 만큼을 반복하였을 때, 노드 개수 - 1번 했을 때와 값이 달라진다면 음의 사이클이 있는 것으로 판별할 수 있음.

코드

다음의 코드는 백준 1865 웜홀의 코드임.

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.StringTokenizer;

public class Main {
    private static final int INF = 100_000_000;

    private static int n;
    private static int[] dist;
    private static List<Node>[] list;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        int tc = Integer.parseInt(br.readLine());

        while (tc-- > 0) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            n = Integer.parseInt(st.nextToken());
            int m = Integer.parseInt(st.nextToken());
            int w = Integer.parseInt(st.nextToken());

            list = new ArrayList[n+1];
            dist = new int[n+1];
            Arrays.fill(dist, INF);
            for (int i = 1; i <= n; i++) {
                list[i] = new ArrayList<>();
            }

            for (int i = 0; i < m + w; i++) {
                st = new StringTokenizer(br.readLine());
                int from = Integer.parseInt(st.nextToken());
                int to = Integer.parseInt(st.nextToken());
                int dist = Integer.parseInt(st.nextToken());

                if (i < m) {
                    list[from].add(new Node(to, dist));
                    list[to].add(new Node(from, dist));
                } else list[from].add(new Node(to, -dist));
            }
            bw.write(bellmanFord() ? "YES\n" : "NO\n");
        }

        br.close();
        bw.flush();
        bw.close();
    }

    private static boolean bellmanFord() {
        dist[1] = 0;

        for (int i = 1; i < n; i++) { // 노드 개수 - 1번 반복
            for (int j = 1; j < list.length; j++) {
                for (Node nxt : list[j]) {
                    if (dist[nxt.to] > dist[j] + nxt.dist)
                        dist[nxt.to] = dist[j] + nxt.dist;
                }
            }
        }

        for (int i = 1; i < list.length; i++) { // 노드 개수 번째 반복에서 값 비교
            for (Node nxt : list[i]) {
                if (dist[nxt.to] > dist[i] + nxt.dist) return true;
            }
        }
        return false;
    }
}

class Node {
    int to;
    int dist;

    Node(int to, int dist) {
        this.to = to;
        this.dist = dist;
    }
}

참고 링크

https://velog.io/@suk13574/알고리즘Java-벨만-포드Bellman-Ford-알고리즘
https://developer-davii.tistory.com/89
https://roytravel.tistory.com/340