💡PCA (주성분 분석)
- 원래 데이터의 분산을 최대한 보존하는 새로운 축을 찾고, 그 축에 데이터를 projection 시키는 기법
- 차원 축소를 통해 고차원의 데이터를 효과적으로 분석하기 위한 Feature Extraction 중 하나
PCA는 데이터들을 정사영 시켜 차원을 낮춘다면, 어떤 벡터에 데이터를 정사영 시켜야 원래의 데이터 구조를 가장 잘 유지할지 구할 때 사용한다. 이때 데이터 구조를 가장 잘 유지하는 축이 PC(주성분)이 된다.
데이터 구조를 가장 잘 유지한다는 것은 분산이 크다는 말이다. (데이터가 퍼져 있으니 더 잘 표현된다.)
분산은 1차원 공간에서만 적용이 가능하기 때문에, feature 수가 많은 매트릭스에서는 공분산 매트릭스를 통해 판단할 수 있다. 즉, 공분산 매트릭스의 고유 벡터를 구하면 해당 데이터를 대표하는 주성분의 주축(PC)를 알 수 있게 된다.
💡PCA 과정
- 데이터 준비 ( df )
- 데이터 정규화(Normalizing)
from sklearn.preprocessing import StandardScaler
# 객체 생성
scaler = StandardScaler()
df_scaled = scaler.fit_transform( df )- 데이터의 공분산 매트릭스 구하기
참고로 공분산 구할 때 주의해야 할 점이 있다.
np.cov()의 공식 문서를 보면 dataset에 있어서 row와 column의 의미를 알려준다.
_Each row of m represents a variable, and each column a single observation of all those variables
그러므로 dataset을 확인하고 .transpose를 해줘야 할지말지를 결정해야한다.
df_cov = np.cov( df_scaled )- 공분산 매트릭스의 고유값, 고유벡터 계산
eigen_val, eigen_vec = np.linalg.eig( df_cov )- 데이터를 고유벡터에 정사영(projection) 시키기
pc = np.matmul( df_scaled, eigen_val )위 과정을 통해 얻은 PC는 사실 차원이 축소 된 것은 아니다.
PC의 값을 구해준 것일 뿐이라 해당 PC 들 중 일부를 사용하는 것으로 차원 축소를 할 수 있다.
이 전체 과정을 간단하게 정규화 과정 후 사이킷런 라이브러리를 통해 구할 수도 있다.
from sklearn.decomposition import PCA
pca = PCA( n_composition = '사용하고자 하는 주성분의 수' )
pc = pca.fit_transform( df_scaled )PCA를 완료하면 기여울이 높은 순서대로 주성분들이 정렬되어 나온다.
여기서 '기여율' 이란 하나의 주성분이 원 데이터를 얼만큼 잘 반영하는가를 나타내는 값이고, 0~1 사이의 값으로 표현된다.
보통 고차원 데이터의 경우, 기여율 합이 80~90%를 넘는 정도 선까지 활용한다.
기여율 확인하는 방법
ratio = pca.explained_variance_ratio_
# 누적기여율 확인
ratio_cumsum = np.cumsum( raito )💡Scree Plots
- PCA 분석 후 주성분의 수를 결정하기 위해 활용하는 plot.
- x축에 주성분, y축에 해당 주성분에 대응하는 고유값을 연결하며, 보통 그래프가 완만해지는 부분까지의 주성분을 활용한다. (단, 본인의 판단에 따라 바뀔 수 있다.)
스크리 플롯은 다음과 같은 형태를 띄고, 아래 플롯의 경우 3이하의 PC가 유의미하다고 할 수 있다.
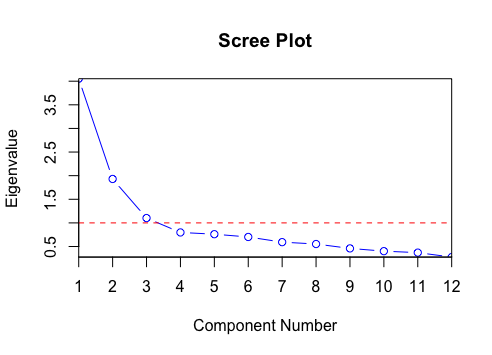
이러한 스크리 플롯을 누적 퍼센트값으로 표현하는 경우도 있다.
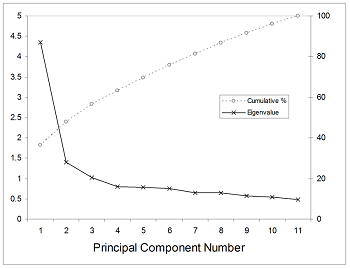
📖Python 예제
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
%matplotlib inline
from sklearn.datasets import make_blobs
from sklearn import decomposition
# Dataset 준비 (random하게 simulation data 생성함)
# 10차원, 표본데이터 수:100, clustser 4개 인 data
X1, Y1 = make_blobs(n_features = 10, n_samples = 100,
centers = 4, random_state = 4, cluster_std = 2)
'''
make_blobs의 반환값
X : [n_samples, n_features] 크기의 배열: 독립 변수
y : [n_samples] 크기의 배열: 종속 변수
'''
# PCA 진행 후 fit
pca = decomposition.PCA(n_components = 4)
pc = pca.fit_transform(X1)
#데이터프레임으로 만들어주며 PC로 변환한 값을 만들어준 뒤 cluster라는 새로운 행을 만듦.
pc_df = pd.DataFrame(data = pc, columns = ['PC1', 'PC2', 'PC3', 'PC4'])
pc_df['Cluster'] = Y1
pc_df.head()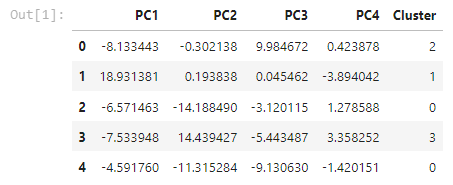
Create the Scree Plot
def scree_plot(pca):
num_components = len(pca.explained_variance_ratio_)
ind = np.arange(num_components)
vals = pca.explained_variance_ratio_
ax = plt.subplot()
cumvals = np.cumsum(vals)
ax.bar(ind, vals, color = ['#00da75', '#f1c40f', '#ff6f15', '#3498db']) # Bar plot
ax.plot(ind, cumvals, color = '#c0392b')
for i in range(num_components):
ax.annotate(r"%s" % ((str(vals[i]*100)[:3])), (ind[i], vals[i]),
va = "bottom", ha = "center", fontsize = 13)
ax.set_xlabel("PC")
ax.set_ylabel("Variance")
plt.title('Scree plot')
scree_plot(pca)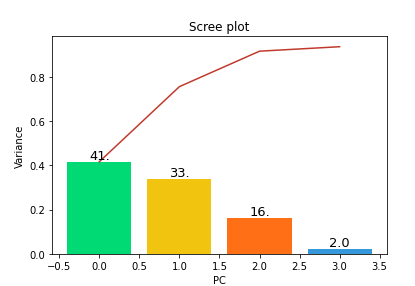
해석 : 10차원의 데이터를 2차원으로 축소했을 때, PC를 3개 고르면 약 90%를 설명할 수 있다.
