섞여있는 데이터들을 어떤 기준에 맞춰 정렬하는 여러종류의 정렬 알고리즘이 있다.
기본적으로 자바스크립트에는 데이터를 정렬해주는 sort()라는 메소드가 존재한다.
하지만 정렬 알고리즘을 공부하는 이유는 데이터의 양이나 상황에 따라 적합하지 않을 수도 있기 때문에 여러 정렬 알고리즘을 상황에 맞게 잘 선택해서 사용해야 하기 때문이다.
대표적인 Bubble sort, insertion sort, merge sort, quick sort 를 알아보자!
Bubble Sort
버블 정렬은 옆에 있는 요소와 비교해서 자신의 위치를 찾아간다.
자신의 위치를 찾아가는 형태가 버블 같다고 해서 버블 정렬이라 한다.
버블 정렬은 한번 순회할 때마다, 가장 오른쪽 끝자리부터 순차적으로 자리를 찾아간다. 기본적으로 데이터의 길이만큼 순회해야 모두 자기 자리를 찾아가게 된다.
예를 들어, 아래와 같은 배열이 있다.
작은 수 부터 큰수로 나열 한다고 했을 때,[4, 6, 3, 2, 8];4, 6을 서로 비교하면
4 < 6이기 때문에 위치에 변화가 없다.[4, 6, 3, 2, 8];6, 3을 서로 비교하면
6 > 3이기 때문에 두 요소의 위치가 바뀐다.[4, 3, 6, 2, 8];6, 2를 비교하면
6 > 2이기 때문에 두 요소의 위치가 바뀐다.[4, 3, 2, 6, 8];6, 8을 비교하면
6 < 8이기 때문에 두 요소의 위치에 변화가 없다.[4, 3, 2, 6, 8];위와 같이 배열의 길이만큼 한번 순회했을 때, 가장 오른쪽 끝
8부터 가장 먼저 자기 자리를 찾게 된다. 이와 같은 방식으로 요소 각각마다 순회를 해야 하기 때문에배열의 길이 ²이 되므로 데이터의 양이 많을수록 성능이 떨어진다.

- 참고 : bubble sort
Big-O
- worst case : O(n²)
- best case : O(n) (이미 정렬이 되어 있는 경우)
장점
in place 추가 공간을 사용하지 않고 주어진 공간만 이용해서 정렬한다. 메모리 공간을 절약할 수 있다. 또 초보자들도 이해하기 쉽고 요소들을 탐색하기 용이하다.
단점
데이터의 양이 많을수록 성능이 떨어진다. 데이터의 길이의 제곱만큼 순회해야 하기 때문에 성능이 좋지 않다. 정렬 중에서도 성능이 좋지 않은 편이다.
bubble sort javascript 구현
아래 소스는 버블 정렬을 알고리즘 구현한 소스이다.
function bubbleSort (array) {
let changeNum;
for (let i = 0; i < array.length; i++) {
for (let j = 0; j < array.length; j++) {
if (array[j] > array[j + 1]) {
changeNum = array[j];
array[j] = array[j + 1];
array[j + 1] = changeNum;
}
}
}
return array;
};
bubbleSort([4, 6, 3, 2, 8]);가장 오른쪽 끝자리부터 자신의 자리를 찾기 때문에 순회할 때마다 가장 끝자리를 제외하며 순회할 수 있도록 아래와 같이 수정하였다.
function bubbleSort (array) { let changeNum; for (let i = 0; i < array.length -1; i++) { for (let j = 0; j < array.length -1 -i; j++) { if (array[j] > array[j + 1]) { changeNum = array[j]; array[j] = array[j + 1]; array[j + 1] = changeNum; } } } return array; }; bubbleSort([4, 6, 3, 2, 8]);
insertion Sort
아래 그림과 같이 삽입 정렬은 왼쪽부터 진행하면서 각각의 요소들을 비교하면서 자기 자기를 찾아간다. 삽입 정렬은 두 번째 자리 숫자부터 뽑아서 그 숫자가 첫 숫자보다 크면 첫 번째 자리 숫자 오른쪽에, 작으면 왼쪽에 넣는다. 세 번째 자리 숫자를 뽑아서 앞의 두 숫자와 크기를 비교해서 알맞은 자리에 넣는다. 이러한 패턴을 반복해서 정렬해 나간다.
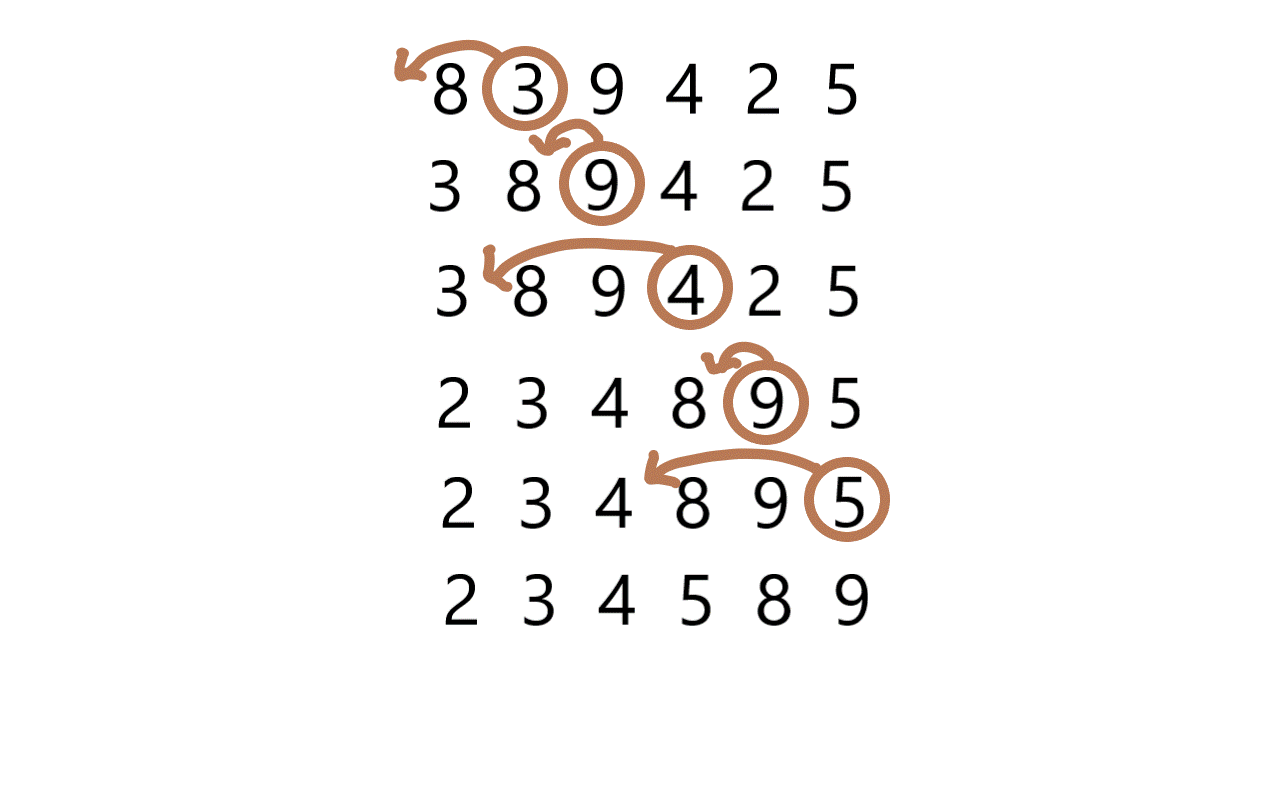
big-O
- worst case : O(n²)
- best case : O(n)
장점
in place 추가 공간을 사용하지 않고 주어진 공간만 이용해서 정렬한다. 메모리 공간을 절약할 수 있다. 또 초보자들도 이해하기 쉽고 요소들을 탐색하기 용이하다.
단점
worst case의 경우 버블 정렬과 마찬가지로 O(n²) 으로 성능이 떨어진다.
insertion sort javascript 구현
function insertionSort (array) {
for (let i = 1; i < array.length; i++) {
let temp = array[i];
let j = i - 1;
while (j >= 0 && array[j] > temp) {
array[j + 1] = array[j];
j--;
}
array[j + 1] = temp;
}
return array;
};
insertionSort([5, 6, 1, 2, 4, 3]);Merge Sort
버블 정렬이나 삽입 정렬보다는 복잡하지만 성능이 좋은 정렬 방법 중 하나이다. 배열을 반씩 잘라 나가면서 하나의 요소로 쪼갠 다음 다시 병합시키면서 정렬해 나간다.
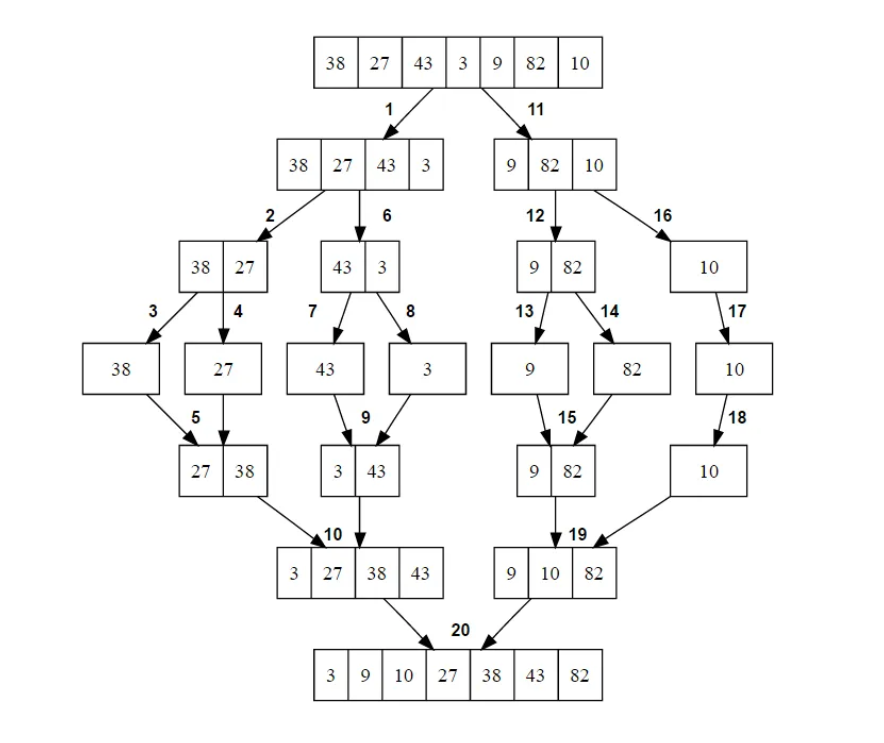
- 참고 : merge sort
big - O
병합 정렬은 분할과 병합 단계로 나뉘는데 분할 단계는 시간 복잡도에 포함되지 않는다. 병합 정렬의 시간 복잡도는 worst case, best case 모두 다 O(n log n)이다.
- worst case : O(n log n)
- best case : O(n log n)
장점
worst case , best case 어떤 경우에도 좋은 성능이 보장된다.
또 중복 값의 위치가 변하지 않는다(stable)
단점
메모리 공간이 필요하다.
분할할 때 데이터 요소의 양만큼 새로운 메모리 공간이 필요하다.
merge sort javascript 구현
const mergeValue = [];
function mergeSort(array) {
if (array.length < 2) {
return array
}
let pivot = Math.floor(array.length / 2);
let left = array.slice(0, pivot)
let right = array.slice(pivot, array.length);
return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right) {
let result = [];
while (left.length && right.length) {
if (left[0].num <= right[0].num) {
result.push(left.shift());
} else {
result.push(right.shift());
}
}
mergeValue.push(result.concat(left, right));
return result.concat(left, right);
}
mergeSort([4,3,6,3,2,1,4,5]);Quick Sort
퀵 정렬은 데이터에서 pivot(기준) 을 정한 뒤 pivot을 중심으로 pivot보다 작으면 왼쪽으로 이동하고, pivot보다 큰면 오른쪽으로 이동한다. 이러한 방법을 왼쪽에 다시 적용하고 오른쪽에도 다시 적용하는 것을 반복해나가면서 정렬한다.
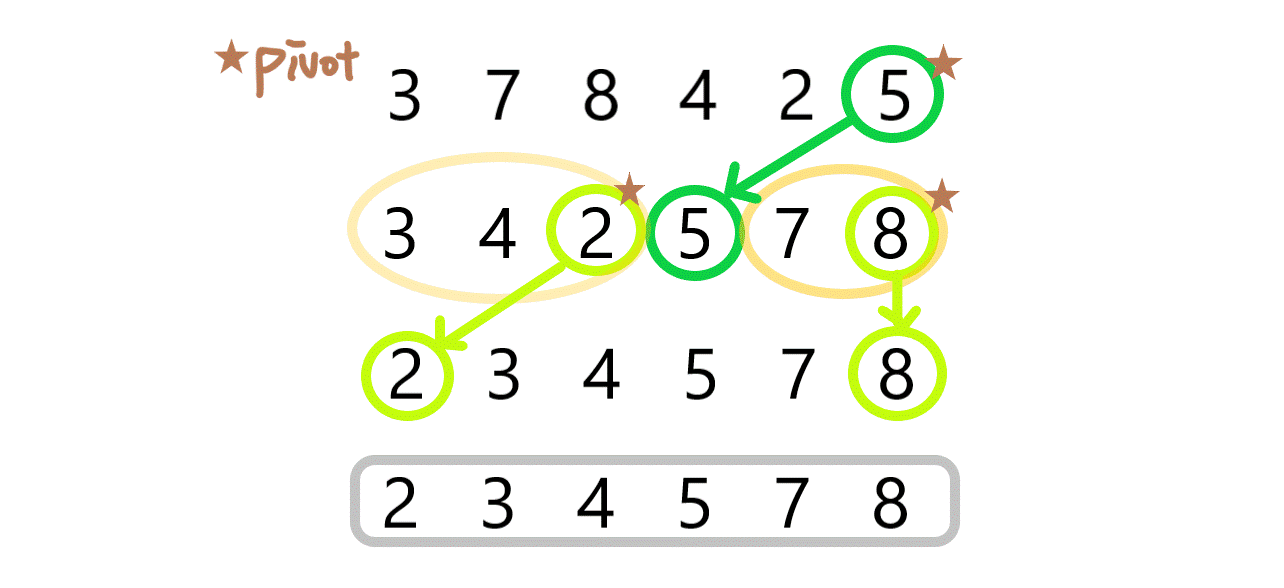
big - O
- worst case : O(n²) (이미 정렬이 되어 있는 경우)
(ex: [1,2,3,4,5] or [5,4,3,2,1]) - best case : O(n log n)
장점
성능이 좋다. in place 추가 공간을 사용하지 않고 주어진 공간만 이용해서 정렬한다. 메모리 공간을 절약할 수 있다. 또 초보자들도 이해하기 쉽고 요소들을 탐색하기 용이하다.
단점
중복값의 위치가 바뀔 수 있는 unstable 정렬방법 이다. pivot의 영향을 받아 worst case의 경우 시간 복잡도가 O(n²) 이된다.
quick sort는 중복 값 위치가 바뀌지 않는 stable 한 방법과 중복 값 위치가 바뀔 수 있는 unstable 한 방법 두 가지가 있다.
stable 한 경우 in place 방법이 아니기 때문에 메모리 공간이 필요하고, unstable 한 경우 in place 방법으로 메모리 공간은 절약할 수 있다. 이러한 이유로 unstable 한 하지만 in place 방법을 더 많이 사용한다.
quick sort javascript 구현
unstable / in place
function partition (array, left, right, pivotIndex) {
let swap;
let pivot = array[pivotIndex];
while (left <= right) {
while (array[left] < pivot)
left++;
while (array[right] > pivot)
right--;
if (left <= right) {
swap = array[left];
array[left] = array[right];
array[right] = swap;
left++;
right--;
}
}
swap = array[left];
array[left] = pivot;
array[pivotIndex] = swap;
return left;
};
function quickSort (array, left = 0, right = array.length -1) {
let pivotIndex = right;
pivotIndex = partition(array, left, right - 1, pivotIndex);
if (left < pivotIndex - 1)
quickSort(array, left, pivotIndex - 1);
if (pivotIndex + 1 < right)
quickSort(array, pivotIndex + 1, right);
return array;
};
quickSort([3,6,5,3,2,5,4,3]);