Tree
나무를 뒤집어 놓은 것처럼 하나의 시작 노드(root)로부터 시작되어 자식 노들(child node)들이 가지를 치듯 뻗어 나가는 구조이다.
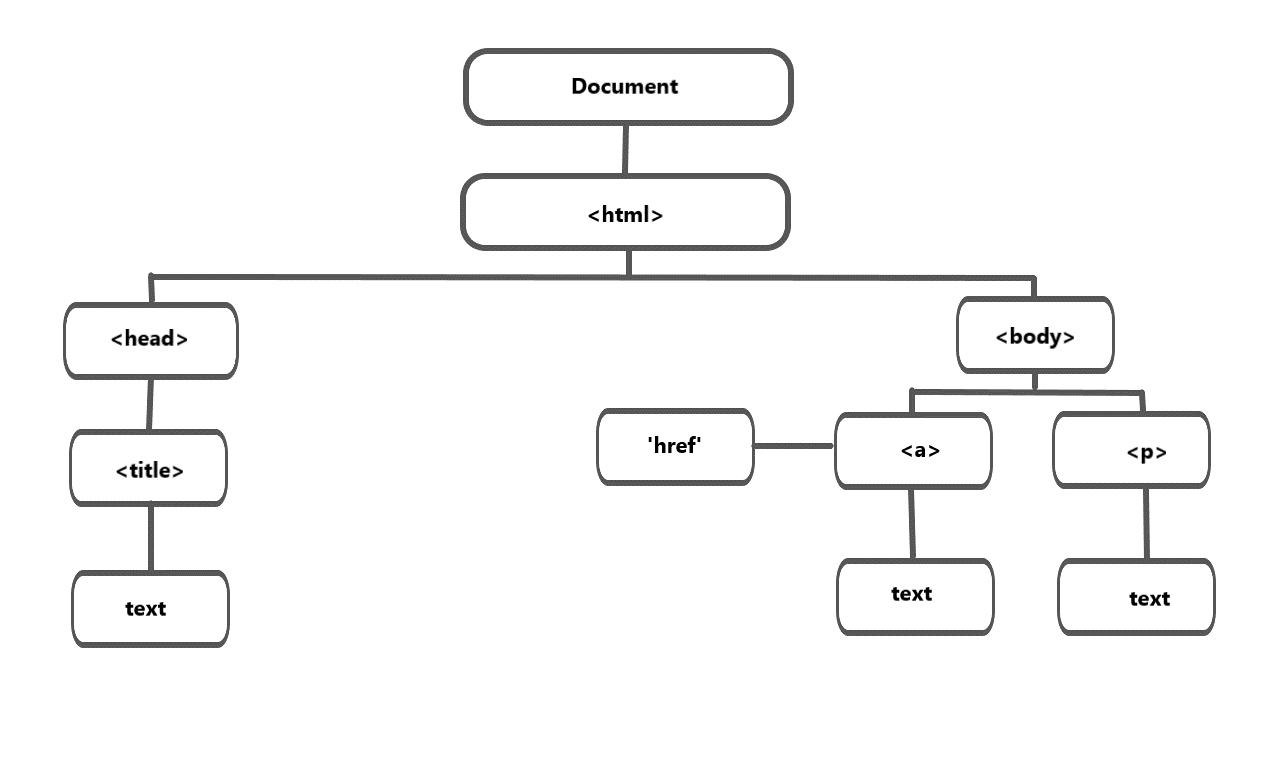
아래 그림과 같이 HTML이 좋은 예이다. root(뿌리)부터 시작해서 아래로 자식 노드들이 뻗어나가는 구조이다.
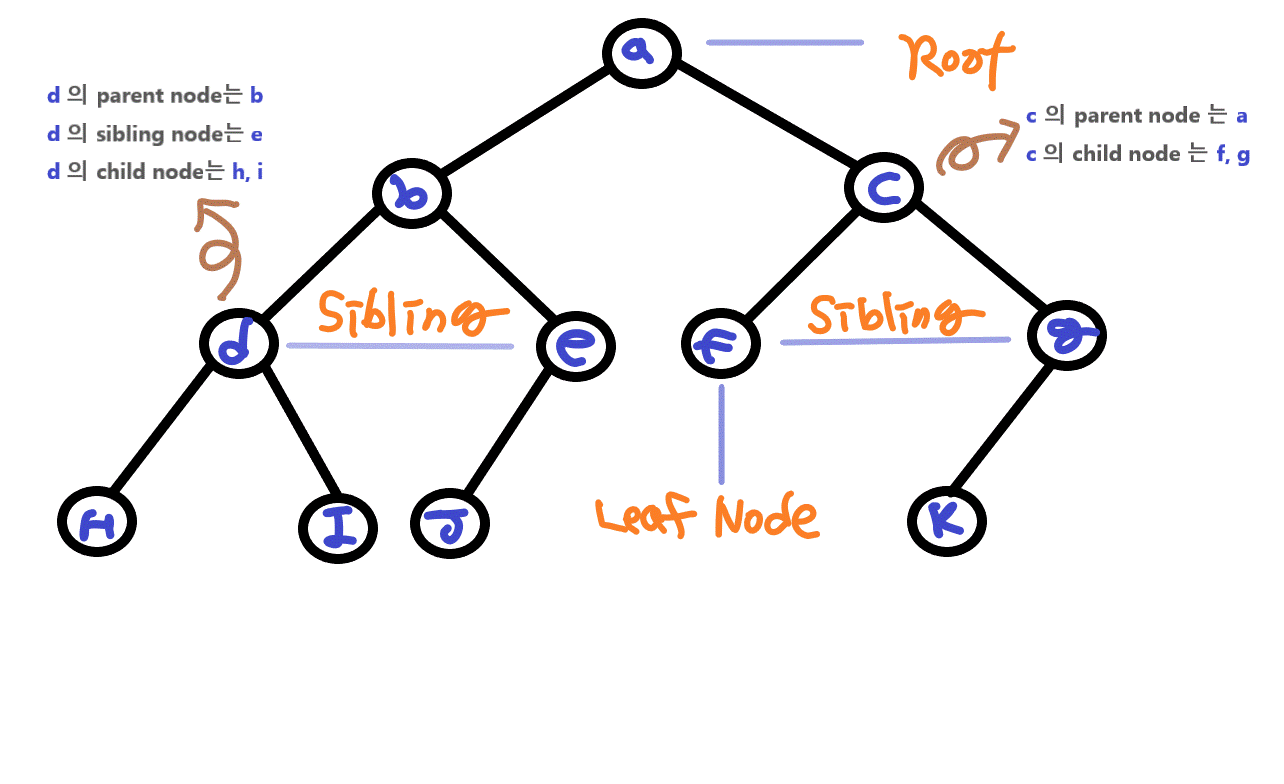
가장 위는root이고 제일 아래를leaf라고 한다. leaf는 자식이 없는 노드이다.
root도 leaf도 아닌 노드들을 내부 노드라고 부른다.
노드와 노드 사이를 이어주는 것을branch나edge라고 부른다.
path는 root에서 child node까지 가는 경로를 말하며,height은
부모 노드에서 자식 노드 사이의 edge 개수를 말한다. 파일 관련 자료를 다룬다면 tree 구조가 적합하다.
Big o
- insertion: O(1)
- Deletion: O(n)
- Search: O(n)
insertion: O(1) / 추가
노드를 추가하려고 할 때, 원하는 위치의 노드에 자식으로 추가해야 할 수 있기 때문에 O(1)이다.
Deletion, Search: O(n) / 삭제, 찾기
삭제할 노드를 찾으려면, 노드를 찾기 위해서 자식 노드들을 차례대로 탐색하면서 내려가야 한다. 최악의 경우 leaf에 존재할 수 있기 때문에 모든 노드를 찾아야하므로 노드를 제거하면 O (n)이된다.
javascript로 Tree 구현
아래는 tree를 구현한 자바스크립트 소스이다.
노드를 자식으로 추가해주고 노드가 포함되어 있는지 확인해주는 기능까지 구현한 소스이다.
var Tree = function (value) {
var newTree = Object.create(treeMethods);
newTree.value = value;
newTree.children = null; // fix me
newTree.children = [];
return newTree;
};
var treeMethods = {};
treeMethods.addChild = function (value) {
var node = Tree(value);
this.children.push(node);
};
treeMethods.contains = function (target) {
var result = false;
function recusion(node) {
if (node.value === target) {
result = true;
return
}
if (node.children.length > 0) {
for (var i = 0; i < node.children.length; i++) {
recusion(node.children[i]);
}
}
}
recusion(this);
return result;
};필요 없는 조건들이 있다는 피드백을 받아 다시 구현한 소스이다.
필요없는 조건들이 있는지 다시한번 생각해봐야겠다.
var Tree = function (value) {
var newTree = Object.create(treeMethods);
newTree.value = value;
newTree.children = [];
return newTree;
};
var treeMethods = {};
treeMethods.addChild = function (value) {
let node = new Tree(value);
this.children.push(node);
};
treeMethods.contains = function (target) {
let result = false;
function recusion(element) {
if (element.value === target) {
result = true;
return;
}
for (let i = 0; i < element.children.length; i++) {
recusion(element.children[i]);
}
}
recusion(this);
return result;
};
Binary Search Tree
트리와 같은 구조로 자식이 2개 이하로만 존재하고 일정한 규칙으로 뻗어나가며 순서가 있는 데이터 구조로 정리되어 있다.(예: 왼쪽은 작은 숫자 오른쪽은 큰 숫자) 이진 검색 트리라고도 한다.
순서가 있는 데이터들을 찾고 넣을 일이 많을 때 binary search tree를 사용한다.
최악의 경우 노드가 한쪽으로만 뻗어 나갈 수 있다.
worst case로 Big-O는 insertion: O(n), Deletion: O(n), Search: O(n)이다. 한쪽으로만 노드가 뻗어나가는 최악의 상황을 대처하기 위해 개량된 트리가 있다.
AVL Tree , red Black Tree 는 한쪽으로만 뻗어 나가지 않게 스스로 균형을 조절한다.
Big o
- insertion: O(log n)
- Deletion: O(log n)
- Search: O(log n)
Big - O : insertion, deletion, search / O(log n) 추가
왼쪽은 작은 숫자, 오른쪽은 큰 숫자로 일정한 규칙으로 정렬되어 뻗어 나간다고 하면, 어떤 노드를 추가하거나 삭제, 검색한다고 하면, 위 그림처럼 왼쪽과 오른쪽 중 기준이 되는 한쪽을 잘라 검색하고 원하는 위치나 찾아야 할 노드가 없다면 또 그것의 반을 잘라 검색해 나가기 때문에 추가, 삭제, 검색 모두 O(log n)이다.
javascript로 Binary Search Tree 구현
아래는 binary search tree를 구현한 자바스크립트 소스이다.
노드를 규칙에 맞는 위치에 추가하고, 노드가 포함되어 있는지 확인하고 트리의 모든 값에 대해 콜백을 실행하는 기능까지 구현한 소스이다.
var BinarySearchTree = function (value) {
var bNewtree = Object.create(BtreeMethod);
bNewtree.value = value;
bNewtree.left = null;
bNewtree.right = null;
return bNewtree;
};
var BtreeMethod = {};
BtreeMethod.insert = function (value) {
var node = BinarySearchTree(value);
function recusion(element) {
if (element.value > node.value) {
if (element.left === null) {
element.left = node;
} else {
recusion(element.left);
}
}
if (element.value < node.value) {
if (element.right === null) {
element.right = node;
} else {
recusion(element.right);
}
}
}
recusion(this);
}
BtreeMethod.contains = function (target) {
var result = false;
function recusion(element) {
if (element.value > target) {
if (element.left.value === target) {
result = true
} else {
recusion(element.left.value);
}
}
if (element.value < target) {
if (element.right.value === target) {
result = true
} else {
recusion(element.right.value);
}
}
}
recusion(this)
return result;
}
BtreeMethod.depthFirstLog = function (func) {
function recusion(element) {
if (element.value) {
func(element.value);
if (element.left) {
recusion(element.left)
}
if (element.right) {
recusion(element.right)
}
}
}
recusion(this);
}
- 코드 스타일!
- value 기존 value와 같은 상황도 고려하면 좋을 것 같다
- 참 -> 거짓 순으로 로직을 작성하는 것이 더 자연스러운 흐름이라고 하셨다.
예를 들어, if (val) {} else {} .- 또, if (element.left === null) 부분도 if (!element.left)로 작성할 수 있다.
- 필요 없는 조건이 아닌지 다시 한번 생각해 보자.
피드백을 받은 부분을 고려해서 다시 작성해 보았다.
앞으로 코드를 작성할 때, 피드백 받은 부분 들을 유념해서 작성해야겠다.
var BinarySearchTree = function (value) {
const bNewtree = Object.create(BtreeMethod);
bNewtree.value = value;
bNewtree.left = null;
bNewtree.right = null;
return bNewtree;
};
var BtreeMethod = {};
BtreeMethod.insert = function (value) {
let node = new BinarySearchTree(value);
function recusion(element) {
if (element.value >= node.value) {
if (!element.left) {
element.left = node;
}
else {
recusion(element.left);
}
}
else {
if (!element.right) {
element.right = node
}
else {
recusion(element.right)
}
}
}
recusion(this);
}
BtreeMethod.contains = function (target) {
let result = false;
function recusion(element) {
if (element.value > target) {
if (element.left.value === target) {
result = true;
return;
}
else {
recusion(element.left.value);
}
}
if (element.value < target) {
if (element.right.value === target) {
result = true;
return;
}
else {
recusion(element.right.value)
}
}
}
recusion(this);
return result;
}
BtreeMethod.depthFirstLog = function (func) {
function recusion(element) {
if (element.value) {
func(element.value);
if (element.left) {
recusion(element.left);
}
if (element.right) {
recusion(element.right);
}
}
}
recusion(this)
}