2022/05/10) 1. 계단오르기 [Dynamic programming(동적계획법)]

1. 문제

<계단오르기>
: 철수는 계단을 오를 때 한 번에 한 계단 또는 두 계단씩 올라간다. 만약 총 4계단을 오른다면 그 방법의 수는 1+1+1+1, 1+1+2, 1+2+1, 2+1+1, 2+2로 5가지다. 그렇다면 총 N계단일 때 철수가 올라갈 수 있는 방법의 수는 몇 가지인가?
(계단의 개수인 N이 주어진다.)

2. 개념

• 동적 계획법은 큰 문제를 작은 단위로 짤라서 해결하는 것이다.
  그리하여 작은 문제의 답을 기록하고 난 후에, 문제의 범위를 넓히는데, 앞에서 구한 답을 이용하여 답을 구하는 것이다. ( = 점화식)
  관계식을 잡아내는 게 핵심이다!

! 오래전에 배웠던 점화식 개념 다시 잡자!

• 점화식은 수열 $a_n$에서 모든 양의 정수 $n$에 대하여 $a_n$을 한 개 이상의 앞선 항들($a_0$, $a_1$, $_...$, $a_{n-1}$ )을 이용하여 나타낸 식이다. 점화식과 함께 처음 몇 개의 항의 값이 주어지면 수열의 모든 항의 값을 구할 수 있다. 이때 처음 몇 개의 항의 값을 준 것을 점화식의 초기 조건이라고 한다.

3. 해결 방법

1. 그림을 그려서 스스로 원리를 이해해보자. 이 부분이 조금 헷갈렸는데, 3계단까지 간다고 할 때, 1계단에서는 +2만 갈 수 있다는 것이였다. 왜 1+1은 못갈까라고 생각했는데, 만약 1+1로 간다고 하면, 0계단에서부터 봤을 때 1+1+1이 된다. 그런데 0계단에서 2계단으로 갈 때 +2 and 1+1로 갔고, 2계단과 3계단은 한 계단만 차이나므로, 결국 1+1+1이 될 수 밖에 없다. 정리하자면 한 방에 가도록 해야 중복이 생기지 않는다. 한 방에 가므로, 2계단에서 4계단으로 가든 3계단에서 4계단으로 가든, 무조건 경우의 수는 1이다. 그러므로 앞에껀 무시하고, 1계단에서 2계단으로, 1계단에서 3계단으로 가는 경우의 수를 구해 더해주기만 하면 되는데, 각 계단에서 이미 다 구했으므로 그냥 앞의 값들을 가져오면 된다.
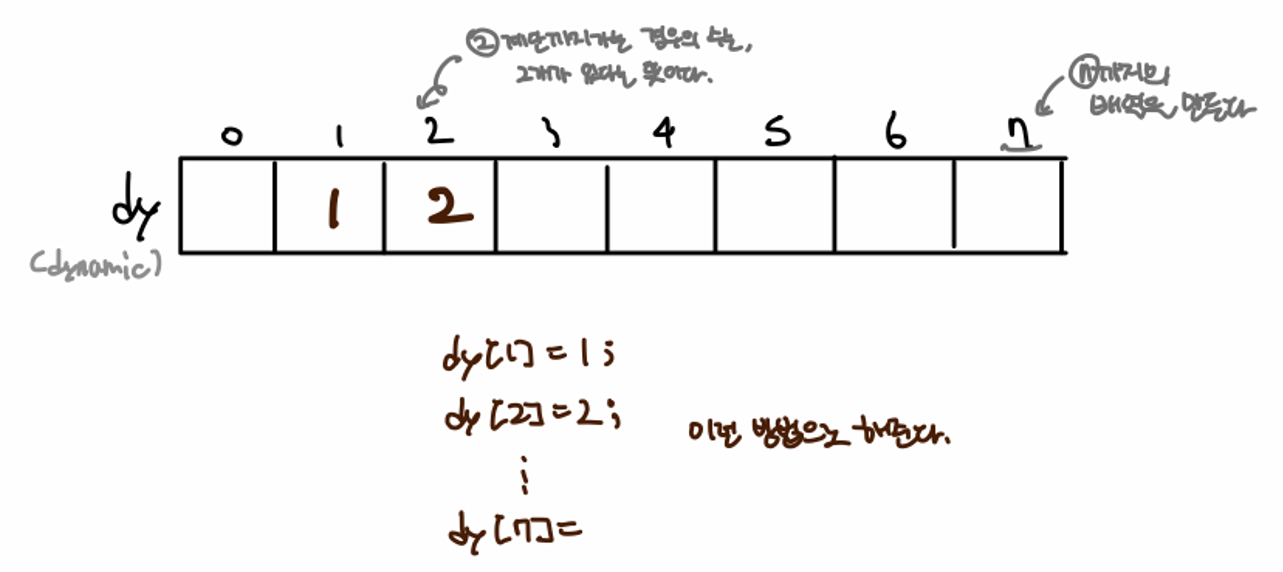
   • 정리하자면, n계단의 경우의 수를 구할 때, n-1계단에서 n계단으로 가는 경우의 수는 1개(한 계단), n-2계단에서 n계단으로 가는 경우의 수는 1개(두 계단) 이므로, 그냥 신경쓰지 말고 제껴두고 (0계단에서 n-1계단으로 오는 경우의 수) + (0계단에서 n-2계단으로 오는 경우의 수)를 해주면, n계단의 경우의 수가 된다.
2. 구한 값들은 dy배열에 넣어준다.
   

4. 정답

        <script>
            function solution(n){  
                let answer=0;
                let dy=Array.from({length:n+1}, ()=>0);
                dy[1]=1; //1계단의 경우의 수
                dy[2]=2; //2계단의 경우의 수
                for(let i=3; i<=n; i++){ 
                    dy[i]=dy[i-2]+dy[i-1];
                }
                answer=dy[n];
                return answer;
            }
            console.log(solution(7));
        </script>