2022/05/13) 4. 동전교환(냅색 알고리즘) [Dynamic programming(동적계획법)]

1. 문제

<동전교환(냅색 알고리즘)>
: 다음과 같이 여러 단위의 동전들이 주어져 있을 때 거스름돈을 가장 적은 수의 동전으로 교환해주려면 어떻게 주면 되는가? 각 단위의 동전은 무한정 쓸 수 있다.
(첫 번째 줄에는 동전의 종류개수 N(1 <= N <= 12)이 주어진다. 두 번째 줄에는 N개의 동전의 종류가 주어지고, 그 다음줄에 거슬러 줄 금액 M(1 <= M <= 500)이 주어진다. 각 동전의 종류는 100원을 넘지 않는다.)
거슬러 줄 동전의 최소개수를 출력한다.

2. 해결 방법

1. dy배열을 생성하여, 동전 1로만 거스름돈을 거슬러줄 때의 동전의 최소 개수를 구한다.
   그리고 동전 1과 2로만 거스름돈을 거슬러줄 때의 동전의 최소 개수를 구하고, 위와 같은 방식으로 동전 1과 2와 5로만 거스름돈을 거슬러줄 때의 동전의 최소 개수를 구한다.
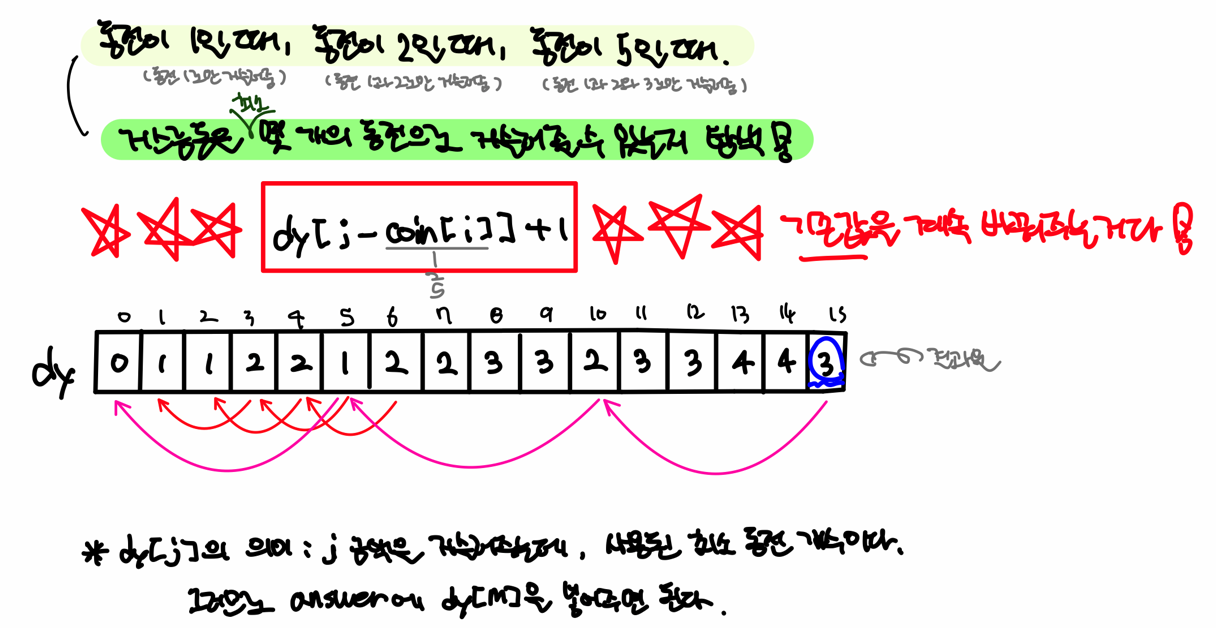
   그러므로 dy배열의 값들을 계속 바꿔준다.(계속 변경되는 dy배열)
2. dy배열의 각 인덱스(dy[j])에는 j 금액을 거슬러 줄 때, 사용된 최소 동전 개수가 들어간다.
   dy[j-coin[i]]+1의 뜻을 이해하는 게 중요한 거 같은데, 내 껄 빼고, 새로운 걸 더한다는 말이다. <5> = 2*2+1 = 5를 보면, 거스름돈 5를 동전2 2개 + 동전1 1개로도 표현할 수 있고, 동전5 1개로도 표현할 수 있다.

3. 정답

        <script>
            function solution(m, coin){
                let answer = 0;
                let dy = Array.from({length:m+1}, ()=>1000); //큰 숫자로 초기화(거스름돈이 500일때, 1원단위의 동전으로만 거슬러주면 500개가 필요하므로, 그냥 넉넉히 1000으로 초기화함)
                dy[0]=0; //거스름돈이 0이니까 거슬러줄 값이 없으니, 0으로 초기화
                for(let i = 0; i < coin.length; i++){ //1원일때, 2원일때, 5원일때
                    for(let j = coin[i]; j <= m; j++){ //5원일때를 보는데, 거스름돈이 1~4라면 조건이 성립하지 않음. 그래서 j의 조건을 저렇게 줌.
                        dy[j] = Math.min(dy[j], dy[j-coin[i]]+1) //최소개수일 경우 넣어주기
                    }
                    //console.log(dy);
                }
                answer = dy[m];
                return answer;
            } 
            let arr=[1, 2, 5];
            console.log(solution(15, arr));
        </script>

4. 소감

어렵다 이해는 됐는데 ㅇ ㅏㅏㅏ