수식과 함께 간단하게 알아보는 LSTM

LSTM

LSTM은 RNN의 문제점인 Gradient Vanishing을 해결하기 위해 등장한 모델 형태로 모든 정보를 저장하려고 했던 RNN과 달리 저장할 정보, 삭제할 정보를 선별하는 기능, cell state라는 또 다른 정보의 저장소가 추가되었습니다.
참고로 이 글은 Long Short-Term Memory Recurrent Neural Network Architectures for Large Scale Acoustic Modeling 논문을 바탕으로 작성한 글입니다.

LSTM의 구조

LSTM 구조의 가장 큰 특징은 각각의 게이트를 통해서 정보를 선별한다는 점입니다.

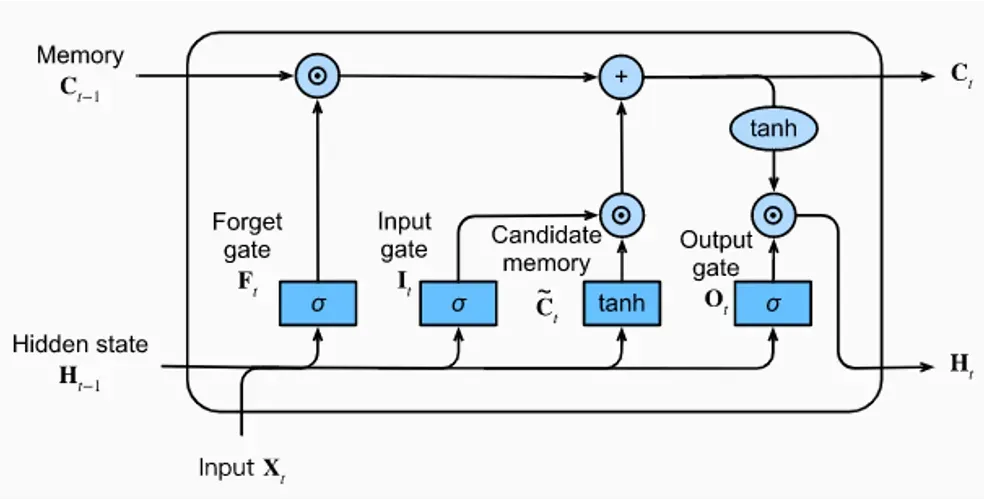
위 그림과 같이 Forget gate, Input gate, Output gate가 존재하는 데, 이 gate들은 각각 해당 정보가 더 이상 필요 없다고 판단하여 삭제할지, 해당 정보를 이후에도 사용할 수 있도록 가져갈 지, 해당 정보를 다음 단계로 얼마나 넘길지를 정하는 gate입니다. 여기서 Input gate와 Output gate가 왜 따로 존재하는지 의문이 생길 수 있는데, Input gate는 cell state로 정보를 입력하고 Output gate는 hidden state로 정보를 입력합니다.

참고로 이 LSTM에서는 cell state라는 또 다른 state를 활용해서 정보를 관리합니다. 이것이 RNN과 LSTM의 차이점으로 LSTM에서는 hidden state(RNN의 hidden state와 동일)와 cell state를 모두 순환시키며 연산에 활용합니다.

RNN에서는 이전 단계에서의 연산 결과만 현재의 연산에 영향을 주었다면 LSTM에서는 이에 더해 cell state라는 전체 연산 단계를 관통하는 state가 하나 더 생긴 것으로 현재까지 등장한 내용을 현재 단계에서 좀 더 잘 반영할 수 있도록 해줍니다.

논문에 등장하는 수식과 의미

Input gate

$i_t = σ(W_{ix}x_t + W_{im}m_{t−1} + W_{ic}c_{t−1} + b_i)$

Input gate에서 cell state로 얼마나 많은 정보를 보낼지 결정하는 수식으로 현재 입력 값($x_t$), 이전 상태의 hidden state( $m_{t-1}$), 이전 상태의 cell state( $c_{t-1}$)에 가중치 행렬과 곱한 후 편향( $b_i$)를 더한 후 시그모이드 함수를 적용하여 0~1 사이의 값으로 나타냅니다. 이때 숫자가 0에 가까울수록 적은 정보를, 1에 가까울수록 많은 정보를 cell state에 보냅니다.

Forget gate

$f_t = σ(W_{fx}x_t + W_{fm}m_{t−1} + W_{f c}c_{t−1} + b_f )$

Forget gate에서 얼마나 많은 정보를 버릴지 결정하는 수식으로 Input gate의 수식과 동일하지만, Input gate의 가중치 행렬이 아닌 Forget gate의 가중치 행렬을 사용합니다. 이 수식의 결과 역시 0~1 사이의 값으로 0에 가까울수록 많은 정보를 버리고 1에 가까울수록 많은 정보를 보존합니다.

Output gate

$o_t = σ(W_{ox}x_t + W_{om}m_{t−1} + W_{oc}c_t + b_o)$

Output gate에서 얼마나 많은 정보를 hidden state로 넘길지 결정하는 수식으로 위의 두 수식과 동일하지만, Output gate의 가중치 행렬을 사용합니다. 위의 두 수식과 동일하게 결과는 0~1 사이의 값으로 0에 가까울수록 적은 정보를, 1에 가까울수록 많은 정보를 hidden state에 보냅니다.

Cell state

$c_t=f_t⨀c_{t−1} + i_t⨀g(W_{cx}x_t + W_{cm}m_{t−1} + b_c)$(⨀ 기호는 element-wise product)

이 식을 좀 더 편하게 설명하기 위해 $g(W_{cx}x_t+W_{cm}m_{t-1}+b_c)$를 $c^ˆ_t$로 치환하면 아래의 수식을 얻을 수 있습니다.

$c^ˆ_t = g(W_{cx}x_t+W_{cm}m_ {t-1}+b_c)$(여기서 함수 $g$는 활성화 함수로 논문에서는 tanh를 사용)

$c_t = f_t⨀c_{t−1} + i_t⨀c^ˆ_t$

Cell state의 값을 update하는 수식으로 이전 상태의 Cell state 값인 $c_{t-1}$과 Forget gate의 계산값인 $f_t$의 element-wise product( $f_t$ 값이 작을 수록 이전 상태를 적게 반영하고 클 수록 많이 반영)한 값과 현재의 정보값 $c^ˆ_t$와 Input gate의 계산값인 $i_t$의 element-wise product($i_t$의 값이 작을수록 현재 정보를 적게 반영하고 클수록 많이 반영)의 합으로 현재 상태의 Cell state 값 $c_t$ 값을 update합니다.

hidden state

$m_t=o_t⨀h(c_t)$(여기서 함수 $h$는 활성화 함수로 논문에서는 tanh를 사용)

현재 상태의 hidden state 값을 구하는 수식으로 현재 상태의 cell state 값 $c_t$와 Output gate의 계산값인 $o_t$의 element-wise product( $o_t$ 값이 작을 수록 적게 반영하고 클 수록 많이 반영)으로 현재 상태의 hidden state 값을 계산합니다.

Output

$y_t = φ(W_{ym}m_t + b_y)$ (여기서 함수 $φ$는 활성화 함수로 논문에서는 softmax를 사용)

현재 상태의 output 값 $y_t$를 구하는 수식으로 현재의 hidden state와 가중치 행렬을 곱한 후 편향( $b_y$)를 더한 후 활성화 함수를 적용하여 값을 계산합니다.

LSTM 수식 코드 구현

# Input gate
i_t = sigmoid(np.dot(x_t, self.Wix)+np.dot(h_prev, self.Wim)+np.dot(c_prev, self.Wic)+self.bi)
# Forget gate
f_t = sigmoid(np.dot(x_t, self.Wfx)+np.dot(h_prev, self.Wfm)+np.dot(c_prev, self.Wfc)+self.bf)
# Cell state
c_hat_t = np.dot(x_t, self.Wcx)+np.dot(h_prev, self.Wcm)+self.bc
c_t = f_t@c_prev+i_t@tanh(c_hat_t)
# output gate
o_t = sigmoid(np.dot(x_t, self.Wox)+np.dot(h_prev, self.Wom)+np.dot(self.ct, self.Woc)+self.bo)
# hidden state
m_t = o_t@tanh(c_t)
# output
y_t = softmax(np.dot(self.W_hy, h_t) + self.b_y)

후기

LSTM 모델의 대략적인 컨셉을 알아보고 논문에 나온 수식을 기반으로 간단하게 해석해 보는 시간을 가졌습니다. 모델을 Numpy만을 활용해 직접 구현해 보는 시간도 가졌었는데 ChatGPT의 도움을 받고서 겨우 완성할 수 있었습니다. 앞으로 많은 연습을 해야 할 것 같습니다.