🧠 데이터 분석가를 위한 심리학-통계학 연결고리: 일상 비유로 보는 냉철한 의사결정

---

1. 🎯 우리의 일상 속 인지 편향과 통계적 오류

데이터를 객관적으로 보는 것을 방해하는 가장 큰 장애물은, 바로 '인간인 우리 자신'입니다. 우리의 뇌는 효율을 위해 '지름길(휴리스틱)'을 사용하며, 이 과정에서 필연적으로 '편향(Bias)'이라는 오류가 발생합니다.

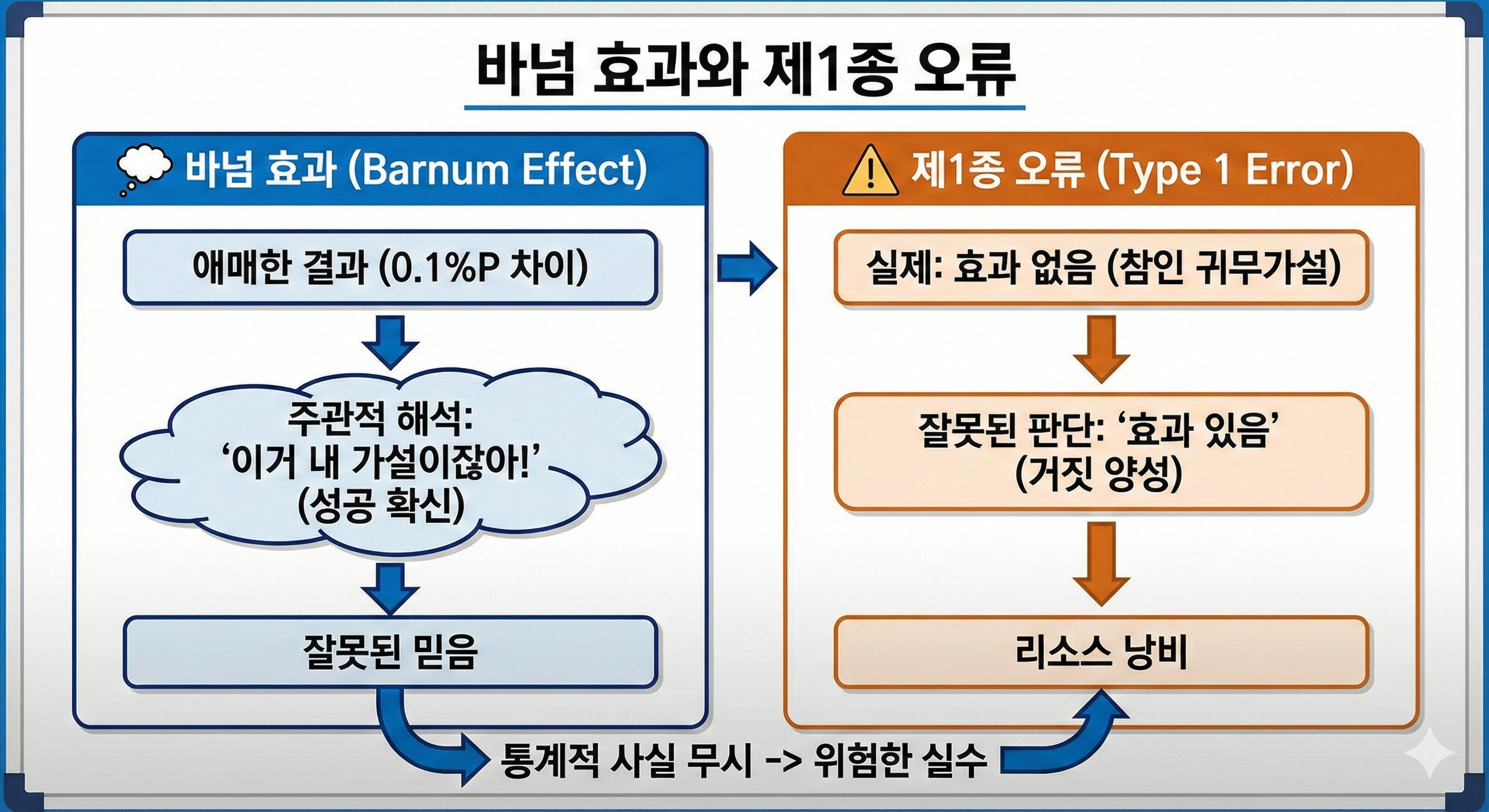
1.1. 🎣 바넘 효과 (Barnum Effect)와 제1종 오류: '나만을 위한 모호한 메시지'의 함정

심리학 용어	일상 비유 (바넘 효과)	통계학 연결
바넘 효과 (Barnum Effect)	MBTI 빙고판 또는 오늘의 운세. "당신은 때로는 외향적이고 때로는 내성적입니다"처럼 누구에게나 해당되는 모호한 묘사를 '나만을 위한 특별한 메시지'라고 믿는 심리.	A/B 테스트의 모호한 결과 (예: P-값 0.3). 통계적으로 차이 없는 0.1%p의 미세한 긍정적 차이를 '우리가 열심히 한 결과'라고 개인적으로 의미 부여하여 채택하려는 경향.
제1종 오류 (Type I Error)	오작동하는 화재 경보기. 실제 불이 안 났는데도 '불이 났다!'고 시끄럽게 울리는 실수.	거짓 양성 (False Positive). 실제로는 A안과 B안에 효과 차이가 없는데도, 분석가가 바넘 효과에 빠져 'A안이 효과가 있다'고 잘못 결론 내리고 적용하는 실수.

연결의 위험성:

분석가는 '0.1%p 상승'이라는 모호한 숫자에 '내 노력'이라는 주관적 가치를 투사합니다. 이는 마치 '당신의 강한 의지가 성공을 부릅니다'라는 모호한 운세가 '나에게만 해당된다'고 믿는 것과 같습니다. 통계적으론 우연일 확률이 30%($\text{P-값} = 0.3$)이지만, 분석가는 자신의 심리적 만족을 위해 이 차이를 '유의미한 효과'로 둔갑시켜 버립니다. 결국 효과 없는 A안을 시장에 배포하는 제1종 오류를 범하게 되죠.

1.2. 🕶️ 확증 편향 (Confirmation Bias)과 데이터 스누핑

심리학 용어	일상 비유 (확증 편향)	통계학 연결
확증 편향 (Confirmation Bias)	내가 좋아하는 연예인의 뉴스만 검색. 좋아하는 연예인의 긍정적인 기사만 보고, 부정적인 뉴스는 '악성 루머'라고 무시하며 믿고 싶은 것만 보려는 태도.	원하는 결론에 맞는 데이터만 선택하거나 가공하는 행위. 자신이 기대했던 가설(예: A안이 좋을 것이다)을 지지하는 지표만 부각하고 반대 지표는 노이즈로 처리.
데이터 스누핑 (Data Snooping)	로또 당첨 번호를 억지로 끼워 맞추기. '만약 이 번호만 바꿨더라면 당첨됐을 거야!'라며 이미 나온 결과를 보고 억지로 규칙을 찾으려는 행위.	P-해킹 (P-Hacking). 원하는 P-값이 나올 때까지 데이터를 계속 쪼개보거나 (세그먼트 변경), 측정 기간을 늘리거나 줄이는 등 통계 분석 방법을 조작하여 유의미한 결과를 억지로 만들어내는 행위.

연결의 위험성:

분석가가 특정 가설에 강한 확신을 가질 때 확증 편향이 발동합니다. '이 A안은 혁신적이야!'라고 믿으면, 데이터를 들여다볼 때 무의식적으로 A안의 성공을 뒷받침하는 지표(예: 신규 사용자 유입)만 선택적으로 봅니다.

더 위험한 것은 데이터 스누핑(P-Hacking)입니다. A/B 테스트 결과, 전체적으로 P-값이 0.1로 유의미하지 않게 나왔다고 가정해 봅시다. 확증 편향에 빠진 분석가는 좌절하지 않고 '어딘가엔 내가 옳다는 증거가 있을 거야!'라며 데이터를 샅샅이 뒤집습니다.

• "여성 사용자 그룹만 보니 P-값이 0.045가 나왔네? 봐! 효과가 있잖아!"
• "주말 데이터만 빼고 보니 P-값이 0.038이 나왔네? 역시!"

이렇게 전체적으로 유의미하지 않은 결과를 억지로 쪼개고 조작해서 0.05 미만의 P-값을 '발견'하는 것이 바로 데이터 스누핑입니다. 이는 사실상 통계적 유의성을 사기 치는 행위와 다름없으며, 발견된 거짓 유의미성은 결국 제1종 오류로 이어집니다.

1.3. 🗄️ 앵커링 효과 (Anchoring Effect)와 초기 기대치의 함정

심리학 용어	일상 비유 (앵커링 효과)	통계학 연결
앵커링 효과 (Anchoring Effect)	첫 가격 제시. 중고 거래 시 판매자가 '원래 100만 원인데, 특별히 80만 원에 드립니다'라고 첫 가격(앵커)을 제시하면, 구매자는 80만 원이 합리적인지보다 100만 원에서 20만 원 깎았다는 사실에 집중하게 됨.	사전 설정된 KPI나 경쟁사 벤치마크. 분석의 초기에 설정된 '기대 성과'나 '경쟁사 수치'가 앵커가 되어, 최종 결과를 객관적으로 해석하지 못하고 그 앵커 근처에 편향되도록 만듦.

연결의 위험성:

분석 프로젝트를 시작할 때, 경영진은 종종 "이번 프로젝트로 전환율을 5%p 올릴 수 있을 겁니다" 또는 "경쟁사는 이미 15%의 전환율을 달성했어요"와 같은 수치를 제시합니다. 이 수치들이 분석가와 의사결정자의 뇌에 강력한 앵커를 박습니다.

A/B 테스트 결과, A안의 전환율이 13%가 나왔다고 가정해 봅시다. 통계적으로는 B안(12%)과 차이가 없을 수도 있습니다 ($\text{P-값} > 0.05$). 그러나 앵커링 효과에 빠진 의사결정자는 이렇게 생각합니다.

1. 앵커 인식: '경쟁사(앵커)는 15%인데, 우리는 아직 13%네. 15%에 도달해야 해.'
2. 주관적 해석: '13%는 12%보다 높으니, A안이 15%로 가는 과정의 첫걸음일 거야. 일단 적용하자.'

이들은 통계적 유의성(객관적 사실) 대신 앵커(주관적 목표)에만 집중합니다. 앵커링 효과는 분석가에게 제1종 오류를 범하게 할 뿐만 아니라, 앵커에 미치지 못하는 모든 결과를 과소평가하게 만들어 제2종 오류까지 동시에 유발할 수 있습니다.

---

2. 🧮 통계학의 방어막: 심리적 함정을 이기는 객관성의 무기

심리학적 함정은 피할 수 없습니다. 하지만 통계학적 원칙은 그 함정에서 벗어나도록 돕는 유일한 방어막입니다. 우리는 통계학 개념을 심리적 편향을 이기는 도구로 이해해야 합니다.

2.1. $\text{P-값}$과 유의 수준 ($\alpha$): '우연의 확률'을 객관적으로 측정하기

통계학 개념	일상 비유	심리학적 방어
P-값 (P-value)	비가 올 확률. "귀무가설(차이가 없다)이 맞다면, 오늘 같은 결과(0.1%p 상승)는 우연히 $\text{P-값}$%의 확률로 발생할 거야."	바넘 효과와 확증 편향에 대항하는 객관적 진실. '내가 원하는' 결과가 아니라, '우연히 일어날' 확률을 보여줌으로써 분석가의 주관을 배제.
유의 수준 ($\alpha$)	경보기 민감도 설정 (예: 5%). "이 정도 확률($5\%$)보다 낮아야만 우연이 아니라고 인정하고 경보를 울리겠다."	제1종 오류의 통제. 분석가의 희망이나 노력과는 관계없이, 통계적으로 수용할 수 있는 최대 실수 허용치를 정하여 제1종 오류의 위험을 사전에 통제함.

연결의 교훈:

P-값과 $\alpha$는 분석가의 감정과 기대를 차단하는 냉정한 방화벽입니다. 분석가가 A안에 대한 확신으로 "0.1%p 차이는 우연이 아니야!"라고 외치고 싶을 때 (바넘 효과), P-값은 "아니, 우연일 확률이 30%야"라고 숫자로 반박합니다.

우리가 $\alpha=0.05$를 설정하는 이유는, '100번 실험 중 5번 정도는 효과가 없는데도 효과 있다고 잘못 판단할 위험은 감수하겠다'는 합리적인 약속을 하는 것입니다. 이 약속을 지키는 것이 곧 제1종 오류를 통제하는 행위입니다.

2.2. 효과 크기 (Effect Size)와 '실용적 유의성'의 균형: 낚시의 비유

통계학 개념	일상 비유	심리학적 방어
효과 크기 (Effect Size)	낚은 물고기의 크기. 낚시꾼이 '물고기를 낚았다(유의미하다)'는 사실뿐만 아니라, '낚은 물고기가 얼마나 크고 실용적인가'를 측정. (예: 1cm짜리 치어 vs. 1m짜리 대어)	P-값 맹신 방지. 통계적으로 유의미한 미세한 차이($\text{P-값} < 0.05$)에 만족하지 않고, 현실적으로 의미 있는 변화인지 묻게 함.
실용적 유의성	낚은 물고기로 식사를 할 수 있는가? 통계적으로 물고기를 낚았지만 (유의미), 너무 작아서 먹을 수 없다면 (실용적이지 않음) 의미 없음.	자원 낭비 방지. 효과 크기가 작다면, A안을 적용하기 위한 개발 비용과 리소스 낭비라는 기회 비용을 따져 제1종 오류의 경제적 손실을 줄임.

연결의 교훈:

P-값은 단순히 '차이가 0이 아닐 확률'만 말해줍니다. 아주 작은 0.001%의 차이라도 데이터가 충분히 많으면 P-값은 0.05보다 작게 나올 수 있습니다. (통계적 유의성 확보)

하지만 분석가는 자문해야 합니다. "이 0.001%의 효과를 위해 A안을 배포할 개발 리소스를 투입하는 것이 경제적으로 합리적인가?"

확증 편향에 빠진 분석가는 "P-값이 0.01이니 무조건 적용해야 합니다!"라고 주장할 것입니다. 이때 효과 크기는 "잠깐, 그 효과가 고작 0.001%라면, 적용해서 얻는 이득보다 개발 비용이 더 클 거야"라고 경고합니다. 이 균형 잡힌 시각은 제1종 오류로 인한 비효율적인 투자를 막아줍니다.

---

3. 🧩 심리학과 통계학의 시너지: 예측과 이해를 동시에

우리의 목표는 단순한 예측이 아니라, 사용자 행동을 이해하고 궁극적으로 개선하는 것입니다. 이를 위해서는 통계적 모델링과 심리학적 해석이 서로를 보완해야 합니다.

3.1. 상관관계 vs. 인과관계: 까마귀 날자 배 떨어진다 (허위 상관)

심리학 용어	일상 비유	통계학 연결
허위 상관 (Spurious Correlation)	까마귀 날자 배 떨어진다. 까마귀가 나는 것(A)과 배가 떨어지는 것(B) 사이에 실제 인과관계는 없는데, 동시에 일어났다는 이유로 관계가 있다고 착각하는 실수.	상관 계수(Correlation Coefficient)의 맹점. 통계적으로는 상관관계($r$)가 높게 나왔지만, 제3의 변수(C, 예: 강한 바람) 때문에 둘 다 발생했을 뿐, A와 B는 서로 영향을 주지 않는 경우.

연결의 위험성:

회귀 분석이나 상관 분석에서 '웹사이트의 폰트 크기(A)'와 '사용자의 구매 전환율(B)'이 $r=0.8$로 강한 상관관계를 보였다고 가정합시다.

확증 편향에 빠진 분석가는 "봐! 폰트 크기를 키우면 구매 전환율이 오르는 거야!"라고 주장하며 폰트 크기 변경에 모든 자원을 투입하려 합니다.

하지만 심리학적 통찰과 통계적 설계(RCT, A/B 테스트)는 '잠깐만!'이라고 외칩니다.

• 심리학적 반박: 사실은 폰트 크기 변경과 함께 '신뢰도 높은 결제 시스템(C)'이 도입되었을 수 있습니다. 폰트 크기(A)가 아니라 결제 시스템(C)이 구매(B)를 올린 진짜 원인입니다.
• 통계적 해결: A/B 테스트(RCT)를 통해 폰트 크기(A) 외의 모든 조건(C)을 통제(Control)하고 랜덤하게 노출시켜야만 인과관계를 추론할 수 있습니다.

허위 상관에 기반한 잘못된 의사결정은 효과 없는 곳에 자원을 투입하는 제1종 오류를 일으킵니다.

3.2. 손실 회피 (Loss Aversion)와 제2종 오류: '잃을까 봐 시도하지 못하는 두려움'

심리학 용어	일상 비유 (손실 회피)	통계학 연결
손실 회피 (Loss Aversion)	무료 체험판 종료 후 결제 고민. 이미 무료로 얻었던 혜택(이득)이 사라지는 것(손실)이, 그 혜택을 처음 얻을 때의 기쁨보다 두 배 이상 고통스러움. 결국 '현재 상태 유지'를 선호.	현상 유지 편향 (Status Quo Bias). 새로운 A안이 기존 B안보다 약간의 이득을 가져올 가능성이 있지만, 혹시라도 B안보다 안 좋을까 봐 (손실 회피) 아예 시도 자체를 꺼리거나, 미묘한 긍정적 결과도 과도하게 보수적으로 해석하여 기회를 놓침.
제2종 오류 (Type II Error)	오작동하는 지진계. 실제 지진이 났는데도 '아무 일 없다'고 경보를 울리지 않는 실수.	거짓 음성 (False Negative). 실제로는 A안이 더 좋았는데도, 분석가가 손실 회피 심리에 사로잡혀 '차이가 없다'고 잘못 결론 내리고 A안 적용 기회를 놓치는 실수.

연결의 위험성:

기업의 의사결정 과정에서 손실 회피는 강력하게 작동합니다.

• 분석가/경영진의 두려움: "A안을 적용했다가 전환율이 조금이라도 떨어지면 (손실) 내가 책임져야 한다." 이 두려움이 합리적인 판단을 마비시킵니다.
• 통계적 보수성: A/B 테스트 결과가 통계적으로 애매하게 유의미할 때 ($\text{P-값}=0.06$, $\alpha=0.05$ 기준 실패), 손실 회피 심리는 "확실하지 않으니 기존(B안)을 유지하자"고 밀어붙입니다.

이러한 보수성은 실제로 효과가 좋았던 A안을 적용할 기회를 영구히 놓치게 만들며, 이는 혁신과 성장의 기회를 포기하는 제2종 오류로 이어집니다. 손실 회피를 이겨내려면 '실패 비용'뿐만 아니라 '성공했을 때의 기회 비용'을 냉철하게 계산해야 합니다.

---

4. 🧭 데이터 분석가, 인지 편향의 선장이 되어라

데이터 분석가는 자신의 심리적 편향이라는 암초를 정확히 인지하고, 통계적 원칙이라는 나침반을 통해 냉철하게 항해해야 하는 선장과 같습니다.

4.1. 습관 1: '나의 가설'과 '귀무가설' 분리하기

• 심리학적 극복: 내가 A안에 대해 긍정적 기대를 가지고 있음을 인정하되, 분석의 목표는 나의 기대를 확증하는 것이 아니라, 귀무가설($H_0$)이 틀렸음을 통계적으로 증명하는 것임을 끊임없이 되새겨야 합니다.
• 통계적 도구: 양측 검정(Two-tailed Test)의 기본 원칙을 고수합니다. 우리가 'A안이 B안보다 좋다'고 생각해도, 통계적 증거는 A안이 B안과 '다르다'는 것만 입증해주면 됩니다. (바넘 효과를 방지하는 객관적 자세)

4.2. 습관 2: 'Power Analysis'로 제2종 오류 최소화하기

• 심리학적 극복: 손실 회피와 제2종 오류를 극복하기 위해, '데이터를 충분히 확보했는지'를 사전에 확인하는 습관을 들여야 합니다.
• 통계적 도구: 검정력 분석 (Power Analysis)을 통해 '만약 실제로 효과가 $\Delta$만큼 있다면, 우리 실험으로 그 효과를 잡아낼 확률이 얼마나 되는가?'를 미리 계산합니다.
  $\text{Power} = 1 - \beta$
  (여기서 $\beta$는 제2종 오류를 저지를 확률입니다.)
  검정력이 너무 낮다면(예: 40%), 실험 기간을 늘려서라도 표본 크기를 확보해야 합니다. 이는 '실제로 좋은 A안'을 '효과 없다'고 놓치는 제2종 오류를 줄이기 위한 가장 과학적인 방법입니다.

4.3. 습관 3: 시각화의 정직성 유지하기

• 심리학적 극복: 시각화는 정보를 가장 빠르게 전달하지만, 앵커링 효과나 확증 편향을 극대화할 수 있습니다.
• 통계적 도구:
  • Y축 0점 시작 원칙: 미세한 차이를 과장하기 위해 Y축을 중간부터 시작하여 차이를 극적으로 보이게 하는 행위(바넘 효과의 시각적 증폭)를 피하고, 0점부터 시작해야 합니다.
  • 적절한 비교: 변화를 보여줄 때 상대적 변화($\%$ 변화)뿐만 아니라 절대적 수치($\#$ 변화)도 함께 명시하여 데이터의 규모를 정직하게 보여줘야 합니다.

---

결론적으로, 데이터 분석의 여정은 숫자를 다루는 동시에 인간의 마음을 이해하는 과정입니다. 바넘 효과는 우리 안의 주관적 소망을, 확증 편향은 우리의 굳건한 신념을, 손실 회피는 우리의 본능적인 두려움을 대변합니다.

우리가 통계적 원칙($\text{P-값}$, $\alpha$, 효과 크기, 검정력)을 고수하는 것은, 이러한 심리적 본능과의 싸움에서 객관성을 지키기 위함입니다. 냉철한 분석가의 자세를 통해 제1종 오류의 덫과 제2종 오류의 기회비용을 모두 회피하고, 데이터 기반의 현명한 의사결정을 내릴 수 있습니다.

---

끝~!@~!#~@!~!@