분할정복

트리미노 퍼즐

• 정사각형이 3개 붙어 있는 것을 트로미노(tromino)라고 한다.
• 가로와 세로로 2^k개의 정사각형이 연결되어 있는 바둑판이 있고,
  1칸은 X 표시가 되어 있다.
  

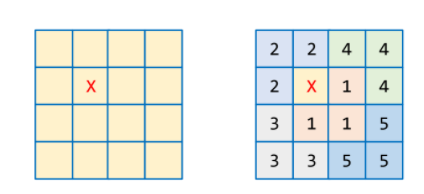
실행코드

• 예시코드를 먼저 보시길 추천합니다.

사이즈 및 크기 조정

def tromino(board, srow, scol, size, xrow, xcol):
  # 사이즈(가로*세로)가 1인 정사각형은 return
  if (size == 1): 
  	return
  
  # ex) srow, scol = 0 이고 size = 4 인 정사각형
  else:
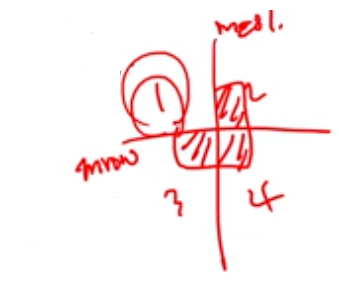
        mrow = srow + (size // 2) # 0+4//2 = 0+2 = 2 
        mcol = scol + (size // 2) # 0+4//2 = 0+2 = 2
        xrow1, xcol1 = mrow - 1, mcol -1 # (1,1) 
        xrow2, xcol2 = mrow - 1, mcol # (1,2)
        xrow3, xcol3 = mrow, mcol - 1 # (2,1)
        xrow4, xcol4 = mrow, mcol # (2,2)

# 1사분면
if (xrow < mrow and xcol < mcol):  # (xrow < 2 and xcol < 2)
  fillCenterExcept(board, mrow, mcol, 1)
  xrow1, xcol1 = xrow, xcol
# 2사분면  
elif (xrow < mrow and xcol >= mcol):  # (xrow < 2 and xcol >= 2)
  fillCenterExcept(board, mrow, mcol, 2)
  xrow2, xcol2 = xrow, xcol
# 3사분면
elif (xrow >= mrow and xcol < mcol):  # (xrow >= 2 and xcol < 2)
  fillCenterExcept(board, mrow, mcol, 3)
  xrow3, xcol3 = xrow, xcol
# 4사분면  
elif (xrow >= mrow and xcol >= mcol):  # (xrow >= 2 and xcol >= 2)
  fillCenterExcept(board, mrow, mcol, 4)
  xrow4, xcol4 = xrow, xcol
  
tromino(board, srow, scol, size // 2, xrow1, xcol1) 
tromino(board, srow, mcol, size // 2, xrow2, xcol2)
tromino(board, mrow, scol, size // 2, xrow3, xcol3)
tromino(board, mrow, mcol, size // 2, xrow4, xcol4)

정사각형 색 채우기

# 위 그림 참조
def fillCenterExcept(board, mrow, mcol, part): # 실행하면 정사각형 3개씩 1개의 번호가 붙음
  global tromino_count
  tromino_count += 1 # 사각형에 부여되는 번호, 번호당 3번씩 사용됨
  
  # 1사분면이 아닌 경우
  if (part != 1): #part=1이면 밑 3개의 if절 실행 -> 2,3,4 분면의 사각형에 번호 1 부여
  	board[mrow-1][mcol-1] = tromino_count # board[2-1][2-1]  
  # 2사분면이 아닌 경우
  if (part != 2): #part=2이면 1,3,4 분면의 사각형에 번호 1 부여
  	board[mrow-1][mcol] = tromino_count # board[2-1][2] 
  # 3사분면이 아닌 경우
  if (part != 3): #part=3이면 1,2,4 분면의 사각형에 번호 1 부여
  	board[mrow][mcol-1] = tromino_count # board[2][2-1] 
  # 4사분면이 아닌 경우
  if (part != 4):#part=4이면 1,2,3 분면의 사각형에 번호 1 부여
  	board[mrow][mcol] = tromino_count # board[2][2] 

def print_board(board):
  for i in range(m): # m=2^k =8 -> 정사각형 개수
    for j in range(m):
      if (board[i][j] < 0): # 처음을 -1(초기값-> 아래 코드에서 설정)로 출력
        print("%3s"%"X", end="") # 'X' 표시

      else:
        print("%3d"%board[i][j], end="") # '번호' 표시

    print()

예시 코드

import random
m = 8 # 2^3
xrow = random.randint(0, m - 1) # (0, 7)
xcol = random.randint(0, m - 1)
print(xrow, xcol)

#초기값
board = [[0] * m for _ in range(m)] # 2차원 배열( m*m = 2^k * 2^k = 8*8꼴)
board[xrow][xcol] = -1 # 위 코드에서'X'로 표시됨
tromino_count = 0

tromino(board, 0, 0, m, xrow, xcol)
print_board(board)

• kdg 때문에 좀 오래걸렸습니다. 죄송합니다.