순열

서로 다른 원소들 중 중복없이 순서에 상관있게 몇개를 뽑아서 나열하는것을
순열이라고 한다.

n개중 r개를 중복없이 순서 상관있게 뽑아서 나열하는 가짓수
nPr = n×(n−1)×(n−2)×⋯⋯×(n−r+1) = n!/(n-r)!

A, B, C 세개의 문자를 중복없이 순서에 상관있게 두개만 나열하면 아래 그림과 같다.

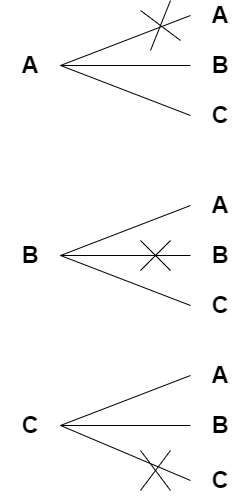
3P2 = 3 * 2 = 6

두 자리가 있는데 첫번째 자리에는 A, B, C세가지가 올수 있고
두번째 자리에는 중복허용을 하지 않으니 첫번째 자리의 문자를 뺀 나머지 두가지가 올수 있다.
따라서 3*2 = 6 이다.

즉
[A, B], [A, C], [B, A], [B, C], [C, A], [C, B]

이걸 이제 자바코드로 짜보자

import java.util.Arrays;
import java.util.Scanner;

public class PermutationTest {

	public static int N, R; 	// nPr 즉 n개의 원소중 r개를 중복 제거, 순서있게 나열하고 싶다.
	public static char[] element, selected; // element는 n개의 원소를 담을 배열, selected는 n개의 원소중 r개를 선택한것을 담을 배열
	public static boolean[] isSelected;	// element의 각원소가 선택이 되었는지 알아보는 배열 선택이 되었으면 true 아니면 false
	
	public static int totalcnt = 0; // 순열의 개수 3P2 = 6에서 6에 해당하는 값
	
	public static void main(String[] args) {

		Scanner sc = new Scanner(System.in);
		System.out.print("nPr에서 n의 개수와 r의 개수가 될것을 입력해주세요(한칸씩 띄어써서 다 썼으면 엔터 눌러주세요) : ");
		N = sc.nextInt(); 
		R = sc.nextInt();
		
		element = new char[N];	
		selected = new char[R];
		isSelected = new boolean[N];
		
		System.out.print("nPr에서 n개의 원소를 입력해주세요(한칸씩 띄어써서 다 썼으면 엔터 눌러주세요) : ");
		for (int i = 0; i < N; i++) {
			element[i] = sc.next().charAt(0);
		}
		
		Permutation(0);
		System.out.println("순열의 총 가짓수 : " + totalcnt);
		
	}
	
	public static void Permutation(int cnt) {	
		
		if(cnt == R) {
			System.out.println(Arrays.toString(selected));
			totalcnt++;
			return;
		}
		
		for (int i = 0; i < N; i++) {
			
			if(isSelected[i] == true) continue;
			selected[cnt] = element[i];
			isSelected[i] = true;
			Permutation(cnt + 1);
			isSelected[i] = false;
		}
	}
}

element배열은 A, B, C를 가지고 있는 char 배열이고
isSelected배열은 element배열과 길이가 똑같은 boolean 배열인데
그 이유는 isSelected 배열의 각 원소가 true냐 false냐에 따라서
element배열의 원소가 선택되었느냐 아니냐가 나타나져있기 때문이다.
당연히 처음엔 A, B, C 아무것도 선택되지 않았으므로 false이고
하나씩 선택하면 true로 변한다.
저 코드에서 [A, A]가 선택되지 않은 이유도

if(isSelected[i] == true) continue;

위코드 덕분이다.

그리고 맨 밑에

isSelected[i] = false;

이 코드는 [A, B], [A, C]를 출력후 B로 넘어갈때 A가 선택되었던것을 지워주는 역할을 하는데
그래서 [A, B], [A, C]를 출력하고 바로 [B, A]가 출력이 가능하게 된것이다.
만일 저 코드가 없었다면 [B, A]는 출력되지 못했을것이다.

중복순열

서로 다른 원소들 중 중복있고 순서에 상관있게 몇개를 뽑아서 나열하는것을
순열이라고 한다.

중복순열과 일반 순열의 가장 큰 차이점은 중복을 허용한다는것이다.
n의 r승으로 표현한다. nΠr = n^r

A, B, C 세개의 문자를 중복있이 순서에 상관있게 두개만 나열하면 아래 그림과 같다.

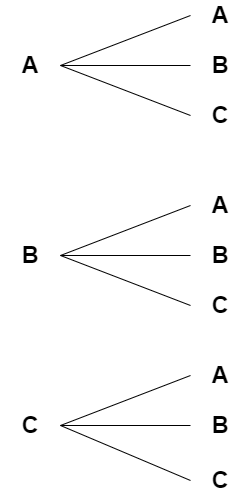
3^2 = 9

두 자리가 있는데 첫번째 자리에는 A, B, C세가지가 올수 있고
두번째 자리에는 중복허용을 하니 첫번째 자리에 있던 문자도 올 수 있다.
따라서 3*3 = 3^2 = 9 이다.

즉
[A, A], [A, B], [A, C], [B, A], [B, B], [B, C], [C, A], [C, B], [C, C]

이걸 이제 자바코드로 짜보자

import java.util.Arrays;
import java.util.Scanner;

// 중복순열 
public class PermutationWithRepetiton {
	
	public static int N, R; 	// nΠr 즉 n개의 원소중 r개를 중복 있이, 순서있게 나열하고 싶다. n^r승
	public static char[] element, selected; // element는 n개의 원소를 담을 배열, selected는 n개의 원소중 r개를 선택한것을 담을 배열
	
	public static int totalcnt = 0; // 중복순열의 개수 3Π2 = 3^2 = 9 에서 9에 해당하는 값
	
	public static void main(String[] args) {

		Scanner sc = new Scanner(System.in);
		System.out.print("nΠr에서 n의 개수와 r의 개수가 될것을 입력해주세요(한칸씩 띄어써서 다 썼으면 엔터 눌러주세요) : ");
		N = sc.nextInt(); 
		R = sc.nextInt();
		
		element = new char[N];	
		selected = new char[R];
		
		System.out.print("nΠr에서 n개의 원소를 입력해주세요(한칸씩 띄어써서 다 썼으면 엔터 눌러주세요) : ");
		
		for (int i = 0; i < N; i++) {
			element[i] = sc.next().charAt(0);
		}
		
		permutation_with_repetiton(0);
		System.out.println("중복순열의 총 가짓수 : " + totalcnt);
		
	}
	
	public static void permutation_with_repetiton(int cnt) {
		
		if(cnt == R) {
			System.out.println(Arrays.toString(selected));
			totalcnt++;
			return;
		}
		
		for (int i = 0; i < N; i++) {
			selected[cnt] = element[i];
			permutation_with_repetiton(cnt + 1);
		}
		
		
	}
}

위의 일반순열 코드에서
isSelected 파트만 지워주면 된다. 굉장히 간단하다.
왜냐하면 중복순열은 중복을 허용하기 때문에 전체 원소중에 어떤것이 선택이 되어서 그 선택된것은 다시 선택하면 안되겠다. 같은 고민을 할 필요가 없기 때문이다.

조합

서로 다른 원소들 중 중복없이 순서에 상관없게 몇개를 뽑는것을 조합이라고 한다.

n개중 r개를 중복없이 순서 상관없게 뽑는 가짓수
nCr = nPr/r! = n!/(n-r)!r! (단 n >= r)

A, B, C 세개의 문자를 중복없이 순서에 상관없게 두개만 뽑아보면 아래 그림과 같다.

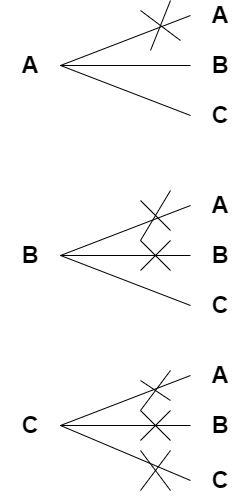
3C2 = 3P2/2! = 3
조합은 이렇게 생각하면 편하다.
A, B, C 세가지 중 두개를 뽑는 조합의 수는
일단 먼저 세가지 중 두개를 순서대로 나열하는 순열인 3P2를 구한다.
그런데 조합은 순서가 없기 때문에 거기에 2! 만큼을 나눈다.
따라서 3P2/2! = 3, 3개이다.

즉
[A, B], [A, C], [B, C]

이걸 이제 자바코드로 짜보자

key point는 [A, B], [A, C], [B, C]에서
항상 오른쪽은 왼쪽보다 (인덱스가)크다는것을 명심하면 된다.

A, B, C 중 두개를 뽑는 문제에서
입력배열은 A, B, C 순서대로 받는다 가정해보자.
그러면 A의 index는 0, B의 index는 1, C의 index는 2이다.
[A, B], [A, C], [B, C]
항상 오른쪽 원소가 왼쪽 원소보다 인덱스가 크다.

만일 입력배열을 C, A, B 순서대로 받는다 가정해보자.
그러면 C의 index는 0, A의 index는 1, B의 index는 2이다.
[C, A], [C, B], [A, B]
항상 오른쪽 원소가 왼쪽 원소보다 인덱스가 크다...

느낌이 오는가..?
이느낌을 살려서 자바로 코드를 짜보자.

import java.util.Arrays;
import java.util.Scanner;

public class CombinationTest {

	public static int N, R; 	// nCr 즉 n개의 원소중 r개를 중복 없이, 순서없게 선택하고 싶다. nPr/r!
	public static char[] element, selected; // element는 n개의 원소를 담을 배열, selected는 n개의 원소중 r개를 선택한것을 담을 배열
	
	public static int totalcnt = 0; // 조합의 개수 3C2 = 3*2/2! = 3 에서 3에 해당하는 값
	
	public static void main(String[] args) {
		
		Scanner sc = new Scanner(System.in);
		System.out.print("nCr에서 n의 개수와 r의 개수가 될것을 입력해주세요(한칸씩 띄어써서 다 썼으면 엔터 눌러주세요) : ");
		N = sc.nextInt(); 
		R = sc.nextInt();
		
		element = new char[N];	
		selected = new char[R];
		
		System.out.print("nCr에서 n개의 원소를 입력해주세요(한칸씩 띄어써서 다 썼으면 엔터 눌러주세요) : ");
		
		for (int i = 0; i < N; i++) {
			element[i] = sc.next().charAt(0);
		}
		
		combination(0, 0);
		System.out.println("조합의 총 가짓수 : " + totalcnt);
	}
	
	public static void combination(int cnt, int start) {
		
		if(cnt == R) {
			System.out.println(Arrays.toString(selected));
			totalcnt++;
			return;
		}
		
		for (int i = start; i < N; i++) {
			selected[cnt] = element[i];
			combination(cnt + 1, i + 1);
		}
		
	}

}

앞에서 말했던 항상 오른쪽 원소의 인덱스가 왼쪽 원소의 인덱스보다 크게 하는 식으로 출력하려면
따로 변수(여기선 start)를 두어서 재귀시 써먹어야한다.

중복조합

서로 다른 원소들 중 중복있고 순서에 상관없게 몇개를 뽑는것을 조합이라고 한다.

n개중 r개를 중복있고 순서 상관없게 뽑는 가짓수
nHr = r+(n-1)Cr = n+r-1Cn-1 (단 n >= r)

A, B, C 세개의 문자를 중복있고 순서에 상관없게 두개만 뽑아보면 아래 그림과 같다.

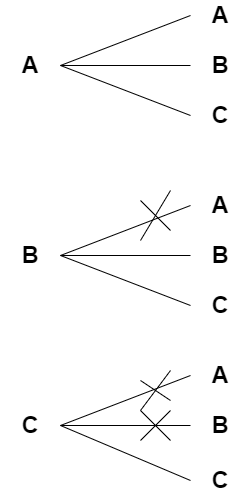
중복조합은 일반 조합에 중복을 허용하는 경우이다.
일반 조합이 주머니에 A, B, C 구슬 세개를 넣어서 한번에 두개를 뽑는것이라면
중복조합은 주머니에 A, B, C 구슬 세개를 넣어서 하나를 먼저뽑은후 다시 주머니에 넣는다. 그리고 다시 뽑는것이다. 이때 순서를 고려하지 않는다면 그것은 중복조합이된다. (만약 이때 순서를 고려했다면 그건 중복순열이다.)
어찌되었건 저 위에 그림에서 A, B, C 세가지 중 두개를 뽑는 중복조합의 수는 공식에 의해
3+2-1C3-1 = 4C2 = 6, 6가지이다.

[A, A], [A, B], [A, C], [B, B], [B, C], [C, C]
이렇게 표현해볼수 있을것이다.

이걸 이제 자바코드로 짜보자.

import java.util.Arrays;
import java.util.Scanner;

public class CombinationWithRepetiton {

	public static int N, R; 	// nHr 즉 n개의 원소중 r개를 중복 있게, 순서없게 선택하고 싶다. 
	public static char[] element, selected; // element는 n개의 원소를 담을 배열, selected는 n개의 원소중 r개를 선택한것을 담을 배열
	
	public static int totalcnt = 0; // 중복조합의 개수 3H2 = 3+2-1C3-1 = 4C2 = 6 에서 6에 해당하는 값
	
	public static void main(String[] args) {
		
		Scanner sc = new Scanner(System.in);
		System.out.print("nHr에서 n의 개수와 r의 개수가 될것을 입력해주세요(한칸씩 띄어써서 다 썼으면 엔터 눌러주세요) : ");
		N = sc.nextInt(); 
		R = sc.nextInt();
		
		element = new char[N];	
		selected = new char[R];
		
		System.out.print("nHr에서 n개의 원소를 입력해주세요(한칸씩 띄어써서 다 썼으면 엔터 눌러주세요) : ");
		
		for (int i = 0; i < N; i++) {
			element[i] = sc.next().charAt(0);
		}
		
		combinationwithrepetiton(0, 0);
		System.out.println("중복조합의 총 가짓수 : " + totalcnt);
	}
	
	public static void combinationwithrepetiton(int cnt, int start) {
		
		if(cnt == R) {
			System.out.println(Arrays.toString(selected));
			totalcnt++;
			return;
		}
		
		for (int i = start; i < N; i++) {
			selected[cnt] = element[i];
			combinationwithrepetiton(cnt + 1, i);
		}
		
	}

}

중복조합코드는 조합코드와 거의 99.9프로 일치한다.
유일한 차이점은 중복조합은 중복을 허용하기 때문에
마지막 combinationwithrepetiton(cnt + 1, i); 에 i + 1 대신 i를 넣는것이다.

부분집합

한 집합의 원소들로만 구성한 집합

집합의 원소가 총 n개일때, 공집합을 포함한 부분집합의 개수는 2^n개이다.
즉, 각각의 원소들을 부분집합에 포함시키거나 포함시키지 않는 두가지의 경우를 모든 원소에 적용한것의 경우의 수와 같다.

A, B, C 세개의 문자의 부분집합을 구해보면 다음과 같다.

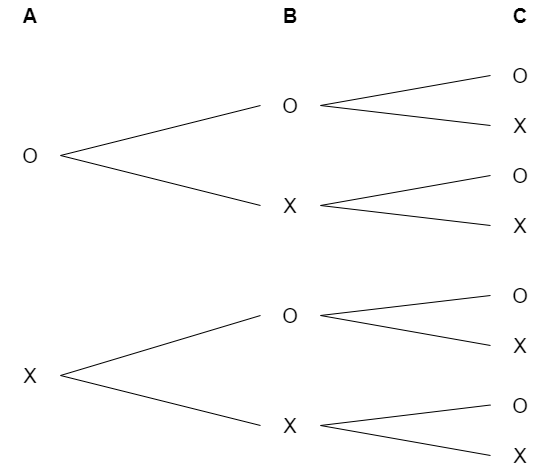
위에 설명에도 적어 놨듯이 부분집합은
각강의 원소들을 부분집합에 포함시키거나 포함시키지 않는 두가지 경우의 수를 모든 원소에 적용한것과 같고
따라서 부분집합의 총 개수는 2^n개이다.
따라서 위 사진에서는

{A,B,C}, {A, B}, {A, C}, {A}, {B, C}, {B}, {C}, { }

으로 총 8개이다.

이걸 이제 자바코드로 짜보자.

import java.util.Scanner;

public class Subset {

	public static int N;	// N은 부분집합을 구하고 싶은 집합의 총 원소의 개수
	public static char[] element;// element는 부분집합을 구하고 싶은 집합의 원소를 담을 배열
	public static boolean[] isSelected;	// element의 각 원소들이 선택되었는지 아닌지를 판단해주는 배열 (위 사진에서) true 이면 O, false이면 X
	
	public static int totalcnt = 0; // 부분집합의 개수
	
	public static void main(String[] args) {
		
		Scanner sc = new Scanner(System.in);
		System.out.print("(부부분집합을 구하고 싶은)집합의 총 원소의 개수를 입력해주세요(다 썼으면 엔터 눌러주세요) : ");
		N = sc.nextInt();
		
		element = new char[N];
		isSelected = new boolean[N];
		System.out.print("(부부분집합을 구하고 싶은)집합의 원소를 입력해주세요(한칸씩 띄어써서 다 썼으면 엔터 눌러주세요) : ");
		
		for (int i = 0; i < N; i++) {
			element[i] = sc.next().charAt(0);
		}
		
		subset(0);
		System.out.println("부분집합의 총 개수 : " + totalcnt);
	}
	
	public static void subset(int cnt) {
		
		if(cnt == N) {
			totalcnt++;
			System.out.print("{");
			for (int i = 0; i < N; i++) {
				
				if(isSelected[i] == true)
					System.out.print(element[i] + " ");
			}
			System.out.println("}");
			return;
		}
		
		isSelected[cnt] = true;
		subset(cnt+1);
		isSelected[cnt] = false;
		subset(cnt+1);
	}

}

isSelected배열을따로 둬서
isSelected배열이 true이면 선택된것, false이면 선택이 되지 않은것을 의미한다.

cnt가 (부분집합을 구하고 싶은)집합의 총 원소의 개수에 다다르면
재귀를 중단시키고
isSelected배열을 순회해서 true이면 선택되었으므로 동일한 인덱스의 element배열의 원소를
출력하고
그렇지 않으면 출력하지 않는다.

부분집합은 주로 knapsack문제에 이용된다. Knapsack문제란
배낭의 용량이 주어지고 각 물건들의 무게와 가격이 주어지고
그 배낭의 용량을 넘지 않는 선에서 어떤 물건을 담아야 가장 가격을 높게 할 수 있냐라는 식이다.

그런데 부분집합을 구할수 있는 코드는
꼭 위와 같은 방식으로 풀지 않아도 된다.

예를들면 아까 위에서 다뤘던
집합 {A, B, C}의 부분집합 {A,B,C}, {A, B}, {A, C}, {A}, {B, C}, {B}, {C}, { }
는 3개짜리 조합({A,B,C}) + 2개짜리 조합({A, B}, {A, C}, {B, C}) + 1개짜리 조합({A}, {B}, {C}) + 0개짜리 조합({ }) 이고
이는 위에서 다루었던 조합코드를 이용해서 코드를 짤 수도 있다.

그 방식대로 코드를 짜보겠다.

import java.util.Arrays;
import java.util.Scanner;

public class Subset2 {

	public static int N;	// N은 부분집합을 구하고 싶은 집합의 총 원소의 개수
	public static char[] element, selected;// element는 n개의 원소를 담을 배열
	public static boolean[] isSelected;
	
	public static int totalcnt = 0; // 부분집합의 개수
	
	public static void main(String[] args) {
		
		Scanner sc = new Scanner(System.in);
		System.out.print("(부부분집합을 구하고 싶은)집합의 총 원소의 개수를 입력해주세요(다 썼으면 엔터 눌러주세요) : ");
		N = sc.nextInt();
		
		element = new char[N];
		isSelected = new boolean[N];
		System.out.print("(부부분집합을 구하고 싶은)집합의 원소를 입력해주세요(한칸씩 띄어써서 다 썼으면 엔터 눌러주세요) : ");
		
		for (int i = 0; i < N; i++) {
			element[i] = sc.next().charAt(0);
		}
		
		for (int i = 0; i <= N; i++) {
			selected = new char[i];
			combination(0, 0, i);
		}
		System.out.println("부분집합의 총 개수 : " + totalcnt);
		
	}
	public static void combination(int cnt, int start, int R) {
		if(cnt == R) {
			totalcnt++;
			System.out.println(Arrays.toString(selected));
			return;
		}
		
		for (int i = start; i < N; i++) {
			
			selected[cnt] = element[i];
			combination(cnt+1, i+1, R);
		}
		
	}

}

위의 부분집합 코드에서 nCr에 해당하는 r을 0부터 n까지 증가시켜서 각각의 조합을 구하면 된다.