참고: https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
합병 정렬을 직접 구현해보았다.
참고해본 블로그에서는 전역변수를 통해서 정렬하는 배열을 활용하였지만, 내가 생각 했던 방법과는 조금 달라서 내 스타일로 조금 바꿔보았음.
계속해서 mid를 기준으로 왼쪽, 오른쪽을 분할한 후에 그 인덱스에 알맞는 배열을 계속해서 획득한 후에 순회를 하며 나열을 했다.
블로그에서 본 전역변수 배열을 사용하면 데이터 크기 면에서 더 이득이 있을까? 라는 고민을 했는데, 어쨋든 왼-오 를 계속해서 분할해 가는 과정과 여기서 데이터가 더 늘어나고 줄어드는 상황은 없어서 데이터 크기는 극적인 차이가 나진 않는 것 같다.
계속 분할, 분할 해서 결국에는 길이가 1인 배열로 분할하고, 그렇게 된다면 left와 right인 덱스의 크기가 같기 때문에 바로 return
return 후에는 왼쪽과 오른쪽에 분할된 배열을 비교하면서 또 합병하며 정렬이 된다.
왼쪽 분할 배열의 순회 인덱스 : left ~ mid (i = left; i <= mid; i++)
오른쪽 분할 배열의 순회 인덱스 : mid+1 ~ right (i = mid+; i <= right; i++)
그리고 코드에서는 새로운 배열을 계속 받아서 쓰기 때문에 인덱스 범위를 둘다 0부터 시작해야해서, 양측에 시작값을 빼줌으로 써 인덱스 범위를 맞춤
left ~ mid -> 0 ~ mid - left
mid+1 ~ right -> 0 ~ right - mid - 1
마지막으로 오른쪽 판단 기준은, 배열의 마지막 인덱스가 되야 하므로 전체 배열의 길이가 5라면 4를 넣어줘야한다.
mergeSort(0, n-1, arr, 0);
static int[] mergeSort(int left, int right, int[] arr, int count){
for(int i = 0; i<count ;i++){
System.out.print(" ");
}
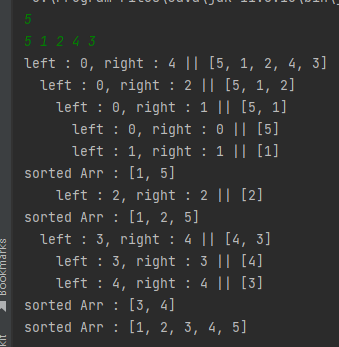
System.out.println("left : " + left + ", right : " + right + " || "+ Arrays.toString(arr));
if(left == right){ // 길이가 1인 경우
return arr;
}
int mid = left + (right - left) / 2;
int lenL = mid - left + 1;
int[] arrL = new int[lenL];
int lenR = right - mid;
int[] arrR = new int[lenR];
System.arraycopy(arr, 0, arrL, 0, lenL);
System.arraycopy(arr, mid - left + 1, arrR, 0, lenR);
int[] sortedArr = new int[lenL+lenR];
if(left < right){
arrL = mergeSort(left, mid, arrL, count + 1);
arrR = mergeSort(mid+1, right, arrR, count + 1);
int i = 0, j = 0, s = 0;
while(i <= mid - left && j <= right - mid - 1){
if(arrL[i] <= arrR[j]){
sortedArr[s++] = arrL[i++];
}else{
sortedArr[s++] = arrR[j++];
}
}
if(i > mid-left){
for(int r = j; r<= right-mid-1; r++){
sortedArr[s++] =arrR[r];
}
}else{
for(int r = i; i<= mid-left; i++){
sortedArr[s++] =arrL[r];
}
}
}
System.out.println("sorted Arr : " + Arrays.toString(sortedArr));
return sortedArr;
}